

Exemple de grand oral en Mathématiques. La fascinante histoire du nombre Pi. Qu'est-ce que le nombre Pi ? Culture mathématique - Histoire du nombre π ("Pi") Carnets de voyages du nombre pi - Micmaths. Comment a-t-on découvert le nombre Pi ? – Kezako. Le fameux nombre PI. Journée internationale du nombre Pi. Pi et autres. Cet article traite d'un algorithme de calcul de décimale par décimale, et montre comment ce type d'algorithme peut se généraliser au calcul d'autres irrationnels, comme e ou Le problème Tout commence avec un mystérieux programme trouvé sur une messagerie électronique (cf.

L'accélération de la convergence, Jean-Paul Delahaye, Pour la Science 199, mai 1994) qui calcule 2400 décimales de quatre par quatre à une vitesse plutôt impressionnante. Le voici en langage C : long a=10000,b,c=8400,d,e,f[8401],g; main(){for(;b-c;)f[b++]=a/5; for(;d=0,g=c*2;c-=14,printf("%.4ld",e+d/a),e=d%a) for(b=c;d+=f[b]*a,f[b]=d%--g,d/=g--,--b;d*=b);} Le même en Pascal : var a,b,c,d,e,g:longint; f:array[0..8400]of longint; procedure affiche(i:integer); begin if i>999 then write(i) else if i>99 then write('0',i) else if i>9 then write('00',i) else write('000',i); end; (reconnaissons que le C est d'une admirable concision)
Kézako : les secrets de la découverte du nombre Pi. L'univers de Pi - Accueil. L'univers de Pi - Lindemann. Transcendance de e :Soit f(x) un polynôme de degré m à coefficients réels.
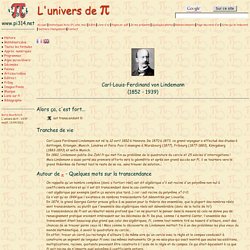
Posons : On intègre m fois par parties et on obtient alors : Maintenant, soit f* le polynôme f où les coefficents ont été remplacés par leur valeur absolue. En majorant les termes dans l'intégrale, on obtient : Ces préliminaires étant écrites, recentrons le débat et supposons e algébrique. En d'autres termes, supposons qu'il existe un entier n>0 et q1,...,qn non nuls tel que : q0+q1e+... +qnen=0 La suite consiste à construire J=q0I(0)+q1I(1)+... L'Univers de Pi - The World of Pi. The Pi Song.
Pi. Un article de Wikipédia, l'encyclopédie libre.
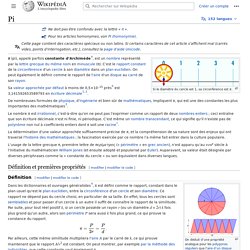
Cette page contient des caractères spéciaux. Si certains caractères de cet article s’affichent mal (carrés vides, points d’interrogation, etc.), consultez la page d’aide Unicode. Si le diamètre du cercle est 1, sa circonférence est π. Sa valeur approchée par défaut à moins de 0,5×10–15 près[2] est 3,141 592 653 589 793 en écriture décimale[3],[4]. De nombreuses formules, de physique, d’ingénierie et bien sûr de mathématiques, impliquent π, qui est une des constantes les plus importantes des mathématiques[5]. Images des mathématiques. Vous avez sans doute entendu parler du nombre qui intervient dans les formules que l’on apprenait à l’école élémentaire : pour le périmètre du cercle de rayon et pour l’aire délimitée par ce cercle (actuellement cela s’apprend en CM2 pour le périmètre et en 6ième pour l’aire).
Je me souviens aussi des valeurs approchées ( ou ou ) de ce nombre que j’ai apprises au CM1 au cours d’une leçon qui m’a marqué pour la vie. Notre instituteur nous apprit ainsi que le nombre permet de calculer le périmètre de tous les cercles, quel que soit leur rayon, et aussi l’aire des disques qu’ils délimitent. Le plus impressionnant pour moi fut d’apprendre que ce nombre a une infinité de décimales et que personne ne peut en donner la liste ni la décrire. C'est presque pi. Ce qui suit ne constitue pas vraiment un paradoxe.

C'est plutôt un avant-goût des problèmes posés par la définition des nombres réels, qui est source de situations authentiquement paradoxales. Jusqu'où faut-il calculer les décimales de deux nombres pour prouver qu'ils sont égaux ? Quelques centaines, quelques milliers suffisent en général à nous convaincre de leur identité. C'est d'ailleurs un moyen utilisé en mathématiques expérimentales pour découvrir de nouvelles formules qui sont ensuite (très souvent) vérifiées rigoureusement. Pi history - MacTutor History of Mathematics. A little known verse of the Bible reads And he made a molten sea, ten cubits from the one brim to the other: it was round all about, and his height was five cubits: and a line of thirty cubits did compass it about.

(I Kings 7, 23) TP Resume Approximation de pi Archimede. Calculer Pi avec Buffon - Math&Magique #8. Autour du nombre pi. Formule de Machin. La formule de Machin fut découverte en 1706 par John Machin et relie le nombre π à la fonction trigonométrique arctangente : Cette formule permet de calculer une approximation du nombre π grâce au développement en série entière de la fonction arctangente.
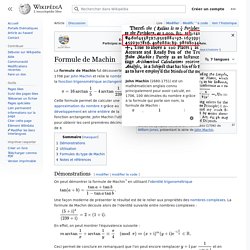
John Machin l'utilisa pour obtenir les cent premières décimales de π. Démonstrations[modifier | modifier le code] On peut démontrer la formule de Machin[1] en utilisant l'identité trigonométrique. En route vers les décimales de Pi : partie 1 - découvrons les formules de MACHIN. Construction de Pi méthode Kochansky. Pseudo-quadrature de Kochanski (1685) – Un peu de mathématiques.
Kochanski - Mathématique Pour Tout Le Monde. Le fameux nombre PI. Comment a été découvert le nombre Pi ? - Vidéo Maths. Mathématiques : le nombre pi - Spécialités. Comme tous les nombres irrationnels, on ne peut qu'approcher la valeur exacte de π, et même si, aujourd'hui, on calcule près de 1 250 000 000 000 décimales, le nombre n'a pas fini de dévoiler tous ses secrets.
À quoi correspond Pi ? Π correspond, d'après la définition, au rapport du périmètre P d'un cercle sur deux fois son rayon r (son diamètre donc) et également, au rapport de la surface S du disque au carré du rayon r d'un cercle. En géométrie euclidienne, ces rapports P/2r ou S/r² sont toujours constants, ils correspondent au nombre π. π est utilisé notamment pour calculer les surfaces des disques ou des volumes des sphères. L'histoire du nombre π va consister à approcher au plus juste sa valeur, en cherchant toujours plus de décimales.
Le Papyrus Rhind Il y a près de 4000 ans, les Babyloniens arrivent au nombre de 3,125. Le nombre Pi - Petits contes mathématiques. NOMBRE PI. Le calcul de pi. « Savoir que la 293ème décimale du nombre pi est un 7 ne m'intéresse pas.
Mais savoir quel est le raisonnement ou la méthode qui a permis de la trouver, voilà qui m'intéresse davantage. » (Albert Jacquard, Sciences et avenir 674, avril 2003) Les décimales de pi. Il existe heureusement des moyens mnémotechniques de retenir ces décimales : il s'agit de retenir des phrases dont les mots ont autant de lettres que les décimales successives (un mot de dix lettres donne la décimale 0) de pi.

Voici par exemple un poème connu permettant de trouver les 127 premières décimales : Et bien sûr, cette méthode est aussi utilisée à l'étranger : voici quelques exemples Sources :WikipédiaDes trucs et des maths. Tout est dans Pi ! Certains nombres sont beaucoup plus riches que d’autres. Quand on regarde l’écriture des nombres sous forme décimale, certains n’ont qu’un nombre fini de chiffres après la virgule, par exemple alors que d’autres peuvent en avoir un nombre infini, par exemple. Parle des décompositions surprenantes de Pi en fractions continues. L'équation du soir 2/6 - Jérôme Pérez - Univers Convergents 2018. Le nombre Pi. Qu'est-ce que le nombre p ? "p = 3,14" comme on dit ... Mais qu'est-ce que ce nombre p ( pi ) au juste ? Pour le commun des mortels ... Tout le monde (enfin, ... en principe !)
Poeme pour Pi. Si Pi m'était conté..., par Jean Mawhin (UCL) Exercices d’Analyse niveau licence 1 et 2. Retour à la page personnelle de Bernard Parisse. 13.1 Le théorème de Villarceau Dans ℝ3 rapporté à un repère orthonormé Oxyz, on considère C le cercle de centre I=(0,a,0) et de rayon r (0<r<a). Histoires autour de la salle Pi - visite générale - version française. 1 - Rio, le Louvre et la Salle Pi par Pierre AUDIN Lire la transcription de l'audio 01Fermer la transcription de l'audio 01 1 - Rio, le Louvre et la Salle Pi par Pierre AUDINBonjour.
Je suis Pierre Audin, médiateur scientifique en mathématiques. Un dimanche soir, je me dirige vers mon bureau auquel j’accède par la Salle Pi. Là, je vois un homme qui filme avec une caméra et un projecteur… Je m’approche et je commence à discuter avec lui. Tout le monde à Rio sait qu’au Louvre il y a une Salle Pi. Théorème d'Hermite-Lindemann.
Un article de Wikipédia, l'encyclopédie libre. Le théorème d’Hermite-Lindemann affirme que pour tout nombre algébrique a non nul, le nombre ea est transcendant. Il fut démontré en 1882 par Ferdinand von Lindemann[1]. En 1885, Karl Weierstrass en donna une généralisation, connue sous le nom de théorème de Lindemann-Weierstrass. TPE PI. CH95 Décimales de PI Leibniz Euler Machin 1 / 1, programmation, décimales, convergence, python. Encadrement de Pi. Archimède et encadrements de Pi. Calculer 1000 décimales de π en moins de 2 secondes. DIFFERENCE D'ARCTANGENTES ET CALCUL APPROCHÉ DE π. Estimation de pi par les aiguilles de Buffon. Une valeur approchée de Pi par la méthode de Buffon. Π et la Méthode de Buffon Voir aussi : Archimède π Eurêka et Monte-Carlo TRICOTIN Que donc est tout cela, mon éminent ami ?
Calculer Pi avec Buffon - M&M #8. Pi-Day : les aiguilles de Buffon. 25 L’aiguille de Buffon. Résumé : Buffon, naturaliste français, a entrepris une expérience étonnante. Il a jeté des aiguilles sur un parquet constitué de lames parallèles puis, il a comptabilisé le nombre de fois où les aiguilles sont tombées à cheval sur deux lames. En route vers les décimales de Pi : partie 1 - découvrons les formules de MACHIN. Python: une méthode de Monte Carlo pour pi. Calcul de Pi selon Brouncker. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Brouncker conjectura, à partir de la formule de Wallis, la fraction continue suivante calculant le nombre π, prouvée par Lambert : L'objectif est ici de calculer une approximation de cette fraction continue, que nous notons F, en établissant un algorithme accessible à la programmation en JavaScript et un programme utilisable en ligne.
Programmer le développement d'une fraction continue n'est pas simple. La difficulté réside dans le fait qu'une telle fraction se calcule "à l'envers" : en partant des éléments les plus bas. Cherchons une récurrence dans le développement. On voit, ci-dessus, que dès la seconde fraction (sous le premier 12), si l'on pose : The Most Unusual Ways Pi Shows Up In Mathematics. Song from π! (Studio Version) Pv140 Des chocs à pi : chocs et rebonds pv140. Blog à Maths - Simon Plouffe et le nombre pi. Formule BBP. Valeur de 1 sur pi (1/Π) Retenir les 30 premières décimales de Pi. Il existe un moyen mnémotechnique pour retenir les trente premières décimales de p. The Best Explanation of Pi. Pi hiding in prime regularities. Le theoreme de Wantzel (Pi n'est pas constructible à la règle et au compas) [CM#3] Irrationalité de π. NL IRRATIONALITE DE PI. DEUX NOMBRES IRRATIONNELS : e et π.
The Discovery That Transformed Pi. Chuck Norris connaît la dernière décimale de π. Sám u sebe v hlavě magického pí číslic deset mám. #LaPiHour. L'existence de Pi. Pi intégrales elliptiques.