Fraction continue. En mathématiques, une fraction continue ou fraction continue simple ou plus rarement fraction continuée[1] est une expression de la forme : comportant un nombre fini ou infini d'étages. On montre qu'on peut « représenter » — en un sens qui sera précisé — tout nombre réel sous forme d'une fraction continue, finie ou infinie, dans laquelle a0 est un entier relatif et les autres aj sont des entiers strictement positifs. Comme dans la notation décimale usuelle, où chaque réel est approché par des nombres décimaux de plus en plus précisément au fur et à mesure de la donnée des décimales successives, de même chaque réel est approché par des fractions étagées de la forme ci-dessus de plus en plus précisément au fur et à mesure qu'on rajoute des étages. En outre, s'il faut une infinité de décimales pour décrire exactement un nombre non décimal, il faut un développement infini en fraction continue pour décrire exactement un nombre irrationnel.
Tour d'horizon[modifier | modifier le code] où et. EPISODE 09 - Introduction aux fractions continues. Les fractions continues. Aujourd’hui je voudrais vous parler d’une construction mathématique très jolie et injustement méconnue : les fractions continues. Vous allez voir que les fractions continues sont à la fois simples, amusantes, belles et utiles ! Que demander de plus ? Pi, ça vaut combien en gros ? Même si vous n’êtes pas un super-geek, il est vraisemblable que vous connaissiez au moins les quelques premières décimales du nombre. . , c’est un truc pratique mais forcément imparfait. . , par exemple Les fractions continues, c’est une autre manière de représenter et d’approximer des nombres réels, une alternative à l’écriture décimale. Pour commencer, si on veut approximer et qu’on est vraiment fainéant, on peut décider de laisser tomber les chiffres après la virgule et simplement dire que C’est un peu cru, alors voyons ce que l’on peut faire de mieux. est égal à 3, plus un petit quelque chose On peut décider de prendre l’inverse de ce petit quelque chose et donc d’écrire Voilà qui est mieux que de simplement dire que . .
Un début de fraction continue ... Fractions continues Texte A Bruguieres. Développement d'un nombre en fraction continue. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges De tout temps les mathématiciens ont voulu donner des approximations rationnelles des nombres qu'il manipulaient, comme les radicaux ou le nombre π. Les premiers usages d'approximation par fraction continue se rencontrent chez Aryabhata, Chuquet puis Wallis auquel on doit, semble-t-il, l'appellation.
Huygens, était intéressé par le sujet pour la construction d'horloges astronomiques de grande précision car outre ses applications en algèbre et en analyse, un exemple pratique de l'usage des fractions continues est la recherche d'un ratio simple dans les problèmes d'entraînement par courroies ou par engrenages.Wallis recherchera des critères de convergence (J. Wallisii Opera Mathematica, 1697-1699). Ainsi π est environ égal à : 3 + 1/7 = 22/7, soit 3,1428... Ainsi π est environ égal à : 3 + 1/(7 + 1/16) = 355/113, soit 3,1415929....
Posons : ! ! Tower of One | Math Challenge | How to solve? Racine de 2 : l’équation de Bombelli – Les éditions des Chavonnes. 1573. On sortait à peine du moyen-âge. Depuis un millénaire, l’église chrétienne avait redoublé d’efforts pour étouffer dans l’œuf le moindre progrès scientifique, consciente peut-être qu’ils pourraient mettre en évidence les mensonges qu’elle déversait sans vergogne sur la population, comme la platitude de la terre ou le géocentrisme. L’étouffoir fut également posé sur les mathématiques. Racine de 2 l’équation de Bombelli Aussi, les seuls progrès notables étaient-ils venus des mathématiciens indiens qui, via Fibonacci, au XIIème siècle, avaient importé en Europe le zéro, le nombres négatifs (auxquels les Grecs étaient allergiques) et système hexadécimal. Article de fond : brève histoire des mathématiques. Seule la théologie connut son heure de gloire. Pourtant quelques lueurs scintillaient encore. Racine de 2 : l’équation de Bombelli L’invention des fractions continues Bombelli savait que √2, qui était la diagonale d’un carré de côté 1, était plus grand que 1 mais inférieur à 2.
WordPress: Phi en Fraction continue. Les fractions continues dans les éclipses, les calendriers et les gammes. The best way to write a fraction?! Les fractions continues au service de la limite. Fractions continues. Collection de nombres, fractions continues, propriétés. Constante de Khintchine (1934) Elle se rapporte à la moyenne géométrique des quotients partiels de la fraction continue. Pour certains nombres irrationnels cette moyenne tend vers une constante K, dite constante de Khintchine (ou Khinchin).
Tous les nombres ne suivent pas cette tendance; notamment les nombres rationnels, les racines des polynômes du second degré à coefficients rationnels et quelques autres (constante e, nombre d'or) . Soit, une faible part des nombres réels. Records de 110 000 décimales en 1998 par X. Gourdon (info de 2010). Formules Fraction continue de Pi Liste des quotients partiels Pi = [3, 7, 15, 1, 292, 1, 1, 1, 2, 1] Produit de ces valeurs Moyenne géométrique pour ces 10 valeurs Moyenne géométrique pour 5 000 valeurs Moyenne géométrique pour une quantité infinie de valeurs Convergence Elle est extrêmement lente! Pour la racine cubique de 10 et 500 termes, on obtient : 2,788… et avec 5000 termes: 2,651… encore loin de la valeur K.
UNE CURIEUSE FRACTION CONTINUE. Fraccont. De l’esthétique des fractions continues (2) 26 janvier 2012 4 26 /01 /janvier /2012 22:07 J'avais déjà parlé de l'article sur Galois dont je suis co-auteur dans BibNum en décembre, à propos des fractions continues, tout à fait fascinantes. Nous avons récemment publié une annexe complémentaire à cet article, intitulé "Quelques variations sur les fractions continues", sous forme de quelques exercices amusants sur la représentation d'un certain nombre (voisin du nombre d'or) en fraction continue. Ce nombre a la propriété de donner 1 quand il est ajoûté à son carré. On demande de démontrer une des formules suivantes, assez amusantes (elles sont toutes trois équivalentes) : Exercez-vous à démontrer ces formules (attention, n'essayez pas de réduire au même dénominateur ! ). Les fractions continues sont passionnantes car c'est un mode de REPRéSENTATION d'un nombre, finalement au même titre que son écriture décimale.
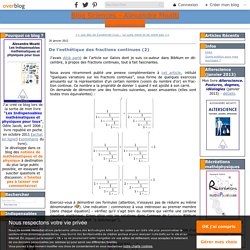
A) 0,618 033.... ? B) 1/2 (√5 – 1) ? C) la fraction continue composée de 1 ci-dessus ? Partager cet article. Démonstration d’un théorème sur les fractions continues périodiques. En 1829, le lycéen Galois (1811-1832) fait paraître son premier article dans les Annales de Gergonne. Il est consacré aux équations et plus précisément aux « fractions continues ».
C’est l’œuvre d’un lycéen qui a lu et assimilé l’œuvre de ses prédécesseurs : Euler et Lagrange en l’espèce. Animé par cette « fureur des mathématiques » et encouragé par son professeur – Paul-Émile Richard (1795-1849) – le jeune homme contacte Gergonne pour faire publier son texte. Dans cet article, l’apport de Galois est analysé et situé dans son contexte mathématique et éditorial (1). Figure 1: L’adresse de l’article de Galois (texte BibNUm, numérisation Numdam) Le premier article de Galois, publié à l’instigation de son professeur En 1828-1829, Galois affecté par son premier échec à l’École polytechnique qu’il avait (mal) préparé avec un an d’avance, intègre la classe de mathématiques spéciales tenue par Louis-Paul-Émile Richard (voir encadré). Les Annales de Gergonne et … les fractions continues alors y = -
Fractionscontinues24 06 2009. Écrire les nombres : développement décimal et fractions continues. C’est bientôt la rentrée, alors on commence à se réchauffer les neurones avec un peu de maths ! La vidéo du jour est un patchwork de petites choses dont j’avais envie de parler Au sujet du développement décimal de la diabolique égalité 0.9999… = 1, la démonstration qui me satisfait le plus est certainement celle qui se base sur une définition du développement décimal sous forme de série dans une base b. où la somme est finie pour les i positifs mais potentiellement infinie pour les i négatifs, ce qui donne le développement décimal « après la virgule ».
Dans ce cas on peut montrer plus formellement que si à partir d’un certain rang (négatif) les sont uniquement des , alors il existe un autre développement décimal fini. Concernant la notion de nombre univers, une petite anecdote. Dans un de mes livres j’ai évoqué cette notion. Je lui ai expliqué que oui, c’était différent, et que la notion de nombre normal était plus forte que celle de nombre univers. (4) Comment écrire les nombres ayant une infinité de décimales ? Constante de Khintchine. Graphe des suites associées à quelques constantes (rouge : π, bleu : γ, vert : 3√2), qui semblent tendre vers cette constante. 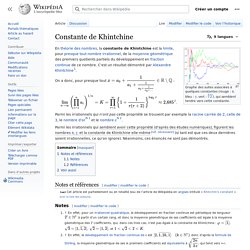En théorie des nombres, la constante de Khintchine est la limite, pour presque tout nombre irrationnel, de la moyenne géométrique des premiers quotients partiels du développement en fraction continue de ce nombre.
C'est un résultat démontré par Alexandre Khintchine[1]. On a donc, pour presque tout Parmi les irrationnels qui n'ont pas cette propriété se trouvent par exemple la racine carrée de 2, celle de 3, le nombre d'or[N 1] et le nombre e[N 2]. Parmi les irrationnels qui semblent avoir cette propriété (d'après des études numériques), figurent les nombres π, γ, et la constante de Khintchine elle-même[réf. nécessaire] (si tant est que ces deux dernières soient irrationnelles, ce qu'on ignore).
Notes et références[modifier | modifier le code] Notes[modifier | modifier le code] Références[modifier | modifier le code] Voir aussi[modifier | modifier le code] Sur la constante de Khintchine. Khintchine. □ Constante de Khintchine : définition et explications. En théorie des nombres, Alexandre Iakovlevitch Khintchine a démontré que pour presque tous les nombres réels x, l'infinité de dénominateurs du développement de la fraction continuée de x a une propriété surprenante : leur moyenne géométrique (La moyenne géométrique d'une série statistique quantitative discrète positive non nulle est...) est une constante, connue sous le nom constante de Khintchine (En théorie des nombres, Alexandre Iakovlevitch Khintchine a démontré que pour presque tous les...), qui est indépendante de la valeur de x.
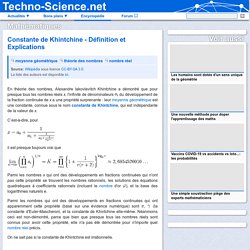
C’est-à-dire, pour il est presque toujours vrai que Parmi les nombres x qui ont des développements en fractions continuées qui n'ont pas cette propriété se trouvent les nombres rationnels, les solutions des équations quadratiques à coefficients rationnels (incluant le nombre (La notion de nombre en linguistique est traitée à l’article « Nombre...) d'or ), et la base des logarithmes naturels e. On ne sait pas si la constante de Khintchine est irrationnelle. Développement de √α en fractions continues et polynômes de Lagrange. Développement de √α en fractions continues et division euclidienne La division euclidienne permet pour un nombre rationnel de trouver son développement en fractions continues.
Nous montrons dans le texte qui suit que c’est également le cas pour une autre famille de nombres réels : les nombres irrationnels de la forme √α, lorsque α est un entier naturel non carré. Hormis le premier, les coefficients du développement apparaissent comme des quotients de divisions euclidiennes. Nous pourrons ainsi, pour cette catégorie particulière de nombres, retrouver de manière élémentaire les principales propriétés du développement. Développement de √α en fractions continues et division euclidienne Les polynômes de Lagrange et leurs secrets Ce texte est la suite de l’article Deux défis de Pierre Fermat dans lequel l’outil du développement en fractions continues d’un irrationnel nous a permis, avec l’aide du logiciel Xcas, de mettre en évidence des solutions de l’équation x2 − αy2=1. PDF - 58.7 ko.
TotDTauIrrational. LAGRANGE, COMTE D’EMPIRE. De la conjecture de Duffin–Schaeffer au théorème de Koukoulopoulos-Maynard. Si le théorème d’approximation de Dirichlet permet d’affirmer qu’il y a une infinité de fractions disponibles lorsque ψ(q)=1q, il s’avère que même une petite variation de ψ peut rendre impossible l’approximation de certains nombres irrationnels α avec la nouvelle contrainte d'erreur.
En juillet 2019, les mathématiciens Dimitris Koukoulopoulos de l’université de Montréal (Canada) et James Maynard du Mathematical Institute à l’université d’Oxford (Royaume-Uni), avait annoncé qu’ils avaient réussi à établir le résultat énoncé sous forme de conjecture par Duffin et Schaeffer dès 1940. Le résultat a été depuis publié dans la revue Annals of Mathematics en juillet 2020. Le théorème obtenu montre essentiellement que la divergence de la série implique l’existence de l’approximation rationnelle.
L’implication inverse est une conséquence du lemme de Borel-Cantelli (celui dans le sens le plus connu). En effet, soit E1,E2,… une suite d’événements dans un espace probabilisé (X,A,λ). Continued Fractions - Professor John Barrow. Fractions continuées et polynômes orthogonaux dans l’œuvre de Laguerre par JEAN DIEUDONNÉ SPHM 1984 9 A1 0. | Sur la réduction en fractions continues d'une fraction qui satisfait à une équation différentielle linéaire du premier ordre dont les coefficients sont rationnels. Laguerre un développement en fractions continues BSMF 1880 8 36 1. Sur la réduction en fractions continues d’une fonction qui satisfait à une équation linéaire du premier ordre à coefficients rationnels Laguerre BSMF 1880 8 21 0.
: mathématiques et sciences physiques en LP. Matrice de Jacobi. Matrice de taille finie[modifier | modifier le code] Les matrices de Jacobi de taille finie sont de la forme avec On montre que est une valeur propre de la matrice si et seulement si Si l'on réduit la fraction continue en une fraction rationnelle, le numérateur sera le polynôme caractéristique de la matrice Dimension infinie[modifier | modifier le code] Considérons deux suites et , toujours avec associé est défini sur un espace de suites par Les opérateurs de Jacobi sont liés à la théorie des polynômes orthogonaux. La solution de alors est un polynôme de degré . Pour tout , si l'on pose . Par exemple, avec , les polynômes sont les polynômes de Laguerre. Avec sont les polynômes de Tchebychev de seconde espèce. Notes et références[modifier | modifier le code] Voir aussi[modifier | modifier le code] Jean Dieudonné, « Fractions continuées et polynômes orthogonaux », dans E.N.
Algorithme d'Euclide [SearchableVideo] Cycles astronomiques et fractions continues. Auteur: Alexandre Pousse Introduction Les fractions continues ont une très longue histoire car liées à celle des nombres. En effet, il existe un lien important entre celles-ci et l'algorithme d'Euclide. Plus particulièrement, elles apparaissent dans l'approximation de nombre comme π ou du nombre d'or.
Délaissées pendant un certain temps, elles sont redécouvertes en Europe en 1655 par le mathématicien anglais John Wallis, puis étudiées par la suite par Leonhard Euler qui va apporter de nombreux théorèmes. L'interêt de l'étude des fractions continues est souvent pour l'approximation d'équations diophantiennes. Deux nombres représentant des périodes, et de trouver , deux entiers tels que . Sont irrationnelles ou rationnelles comportant de nombreuses décimales (ce qui est fréquent de manière générale en Physique), on va alors chercher à trouver la meilleure combinaison linéaire approximant .
Définitions et propriétés Une fraction continue est un objet s'écrivant sous la forme où les et les avec et . . Fractions continues. Autour de l’arbre de Stern-Brocot. Autrement dit : SL2(N)={D,G}∗. Si l'on s'autorise à manipuler des suites infinies de symboles D et G, l'arbre de Stern-Brocot permet d'atteindre tous les nombres réels strictement positifs. Pour ce faire, si x est le réel strictement positif que l'on souhaite atteindre, il suffit d'utiliser le même algorithme que celui présenté à la section 4, permettant de retrouver un rationnel r donné dans l'arbre, en y remplacer r par x. Bien entendu, une conséquence du théorème 5 est que l'algorithme s'arrête après un nombre fini d'étapes si et seulement si x est rationnel.
Par exemple, le chemin menant au nombre d'or ϕ est donné par (D,G,D,G,D,G,D,G,…). Ceci ne surprendra pas les lectrices et lecteurs avertis, puisque si l'on observe les rationnels apparaissant sur les branches de ce chemin, on retrouve les termes Fn+1/Fn, où (Fn)n∈N désigne la suite de Fibonacci, qui convergent vers ϕ. Remerciements. Calcul de Pi selon Brouncker. Pavages, fractions continues et Géométrie discrète thèse Fernique. Exotic formulas of Ramanujan. Category:Continued fractions. Pi.