

Crochet de Lie. Un article de Wikipédia, l'encyclopédie libre.
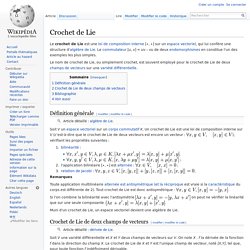
Le nom de crochet de Lie, ou simplement crochet, est souvent employé pour le crochet de Lie de deux champs de vecteurs sur une variété différentielle. Topologie. Un article de Wikipédia, l'encyclopédie libre. un ruban de Möbius est une surface fermée dont le bord se réduit à un cercle.
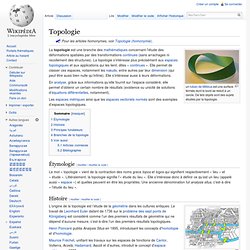
De tels objets sont des sujets étudiés par la topologie. La topologie est une branche des mathématiques concernant l'étude des déformations spatiales par des transformations continues (sans arrachages ni recollement des structures). La topologie s’intéresse plus précisément aux espaces topologiques et aux applications qui les lient, dites « continues ». Elle permet de classer ces espaces, notamment les nœuds, entre autres par leur dimension (qui peut être aussi bien nulle qu’infinie). Algebraic topology. Topologie algébrique. Un article de Wikipédia, l'encyclopédie libre.
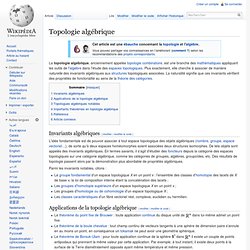
Invariants algébriques[modifier | modifier le code] Parmi les invariants notables, citons : Henri Cartan. Henri Paul Cartan (French: [kaʁtɑ̃]; July 8, 1904 – August 13, 2008)[1] was a French mathematician with substantial contributions in algebraic topology.
He was the son of the French mathematician Élie Cartan[2] and the brother of composer Jean Cartan. Life[edit] Cartan studied at the Lycée Hoche in Versailles, then at the École Normale Supérieure in Paris, receiving his doctorate in mathematics. He taught at the University of Strasbourg from November 1931 until the outbreak of the Second World War, after which he held academic positions at a number of other French universities, spending the bulk of his working life in Paris. Cartan is known for work in algebraic topology, in particular on cohomology operations, the method of "killing homotopy groups", and group cohomology. Jean-Pierre Serre. Jean-Pierre Serre (French: [sɛʁ]; born 15 September 1926) is a French mathematician who made fundamental contributions to algebraic topology, algebraic geometry, and algebraic number theory.
He was the first recipient of the Abel Prize in mathematics. Théorie des catégories. Un article de Wikipédia, l'encyclopédie libre.
Les catégories sont utilisées dans la plupart des branches mathématiques et dans certains secteurs de l'informatique théorique et en mathématiques de la physique. Elles forment une notion unificatrice. Cette théorie a été mise en place par Samuel Eilenberg et Saunders Mac Lane en 1942-1945, en lien avec la topologie algébrique, et propagée dans les années 1960-1970 en France par Alexandre Grothendieck, qui en fit une étude systématique. À la suite des travaux de William Lawvere, la théorie des catégories est utilisée depuis 1969 pour définir la logique et la théorie des ensembles ; elle peut donc, comme cette dernière, être considérée comme fondement des mathématiques. Foncteur. Un article de Wikipédia, l'encyclopédie libre.
En mathématiques, le foncteur est la généralisation aux catégories de la notion de morphisme. Homologie et cohomologie. Un article de Wikipédia, l'encyclopédie libre.
Généralités[modifier | modifier le code] Complexe de chaînes[modifier | modifier le code] Un complexe de chaînes est la donnée d'une suite de groupes abéliens ou plus généralement d'objets d'une catégorie abélienne et d'une famille d'homomorphismes, appelés opérateurs de bord , telle que : Homologie singulière. Un article de Wikipédia, l'encyclopédie libre.
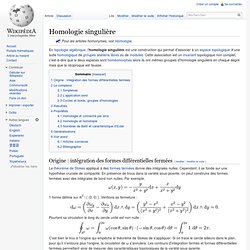
En topologie algébrique, l'homologie singulière est une construction qui permet d'associer à un espace topologique X une suite homologique de groupes abéliens libres ou de modules. Cette association est un invariant topologique non complet, c'est-à-dire que si deux espaces sont homéomorphes alors ils ont mêmes groupes d'homologie singulière en chaque degré mais que la réciproque est fausse. Origine : intégration des formes différentielles fermées[modifier | modifier le code] Le théorème de Stokes appliqué à des formes fermées donne des intégrales nulles.
Cependant, il se fonde sur une hypothèse cruciale de compacité. 1-forme définie sur ℝ2 \ { (0, 0) }. Pourtant sa circulation le long du cercle unité est non nulle : Homologie des groupes. Un article de Wikipédia, l'encyclopédie libre.
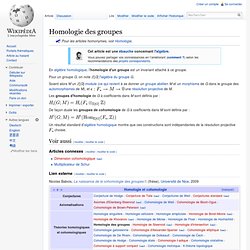
En algèbre homologique, l'homologie d'un groupe est un invariant attaché à ce groupe. Pour un groupe G, on note ℤ[G] l'algèbre du groupe G. Soient alors M un ℤ[G]-module (ce qui revient à se donner un groupe abélien M et un morphisme de G dans le groupe des automorphismes de M), et. Produit fibré. Un article de Wikipédia, l'encyclopédie libre. Définition ensembliste[modifier | modifier le code] le produit fibré de et. Théorie des nœuds. Un article de Wikipédia, l'encyclopédie libre. Pour les articles homonymes, voir nœud. illustration de la théorie des nœuds. Théorie des tresses. Un article de Wikipédia, l'encyclopédie libre. Les groupes de tresses peuvent être définis de différentes manières équivalentes, illustrant les relations qu'ils entretiennent avec différents domaines des mathématiques.
Exemple de tresse à trois brins Soit. Variété topologique. Un article de Wikipédia, l'encyclopédie libre. Définition[modifier | modifier le code] Soit un espace topologique séparé à base dénombrable. On dit que est une variété topologique si : pour tout point. Topologie différentielle. Un article de Wikipédia, l'encyclopédie libre. La topologie différentielle est une branche des mathématiques qui étudie les fonctions différentiables définies sur des variétés différentielles, ainsi que les applications différentiables entre variétés différentielles.
Elle est reliée à la géométrie différentielle, discipline avec laquelle elle se conjugue pour construire une théorie géométrique des variétés différentiables. Description[modifier | modifier le code] La topologie différentielle s'intéresse aux propriétés et aux structures qui requièrent une structure différentiable sur une variété. Les variétés différentiables sont plus « lisses » que les variétés simplement munies de structures géométriques, ces dernières pouvant agir en tant qu'obstructions à certains types d'équivalence ou de déformation qui existent en topologie différentielle. Variété différentielle. Un article de Wikipédia, l'encyclopédie libre. Une variété différentielle se définit d'abord par la donnée d'une variété topologique, espace topologique localement homéomorphe à l'espace. Géométrie différentielle.
Un article de Wikipédia, l'encyclopédie libre. En mathématique, la géométrie différentielle est l'application des outils du calcul différentiel à l'étude de la géométrie. Les objets d'étude de base sont les variétés différentielles, ensembles ayant une régularité suffisante pour envisager la notion de dérivation, et les fonctions définies sur ces variétés. Groupe de Lie. Groupe de Lie E8 clé théorie des supercordes. Le mathématicien Fokko du Cloux. Groupe de Lie E8 : une clé pour la théorie des supercordes ? - 5 Photos Figure géométrique dont la complexe symétrie est codée par le groupe de Lie E8 (Crédit : AIM).
Si vous demandez à des mathématiciens professionnels ce qu'est le groupe de Lie E8, bien peu seront capables de vous répondre.