

Charles-Jean de La Vallée Poussin. Charles-Jean de La Vallée Poussin Baron de La Vallée Poussin Charles-Jean Étienne Gustave Nicolas, baron[N 1] de La Vallée Poussin, né le 14 août 1866 à Louvain en Belgique, mort le 2 mars 1962 à Watermael-Boitsfort, à Bruxelles, est un mathématicien belge.
Il est connu pour avoir démontré[N 2] le théorème des nombres premiers en utilisant les méthodes de l'analyse complexe. Biographie[modifier | modifier le code] Il étudie chez les Joséphites, au collège de la Sainte-Trinité à Louvain, puis comme interne au collège Saint-Stanislas, chez les Jésuites de Mons. Biographie de Charles-Jean de La Vallée Poussin. Charles-Jean de La Vallée Poussin est un mathématicien belge de la fin du XIXè siècle et de la première moitié du XXè siècle.

Il est né le 15 août 1866 à Louvain. Sa famille est issue de la bourgeoisie normande et compte en son sein peintres, officiers, ministres et scientifiques. Entré à l'Université de Louvain en 1883, La Valléee Poussin suit avec brio successivement des études de philosophie, d'ingénierie, avant que les cours de Gilbert ne le tournent définitivement vers les mathématiques. La Vallée Poussin devient assistant de Gilbert en 1891, mais ce dernier décède un an plus tard. LaValleePoussin. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Né à Louvain (Belgique), après des études à Mons, Charles de la Vallée-Poussin est nommé à la célèbre université flamande de Louvain (1892), poste qu'il conserva pendant toute sa carrière.

Il enseigna également au collège de France. Ses recherches portèrent principalement sur l'approximation des fonctions numériques et, en théorie des nombres, tout particulièrement sur les nombres ζ de Riemann, liés aux nombres premiers et à leur raréfaction pour les grandes valeurs de tels nombres. Démonstration du théorème de Bernoulli. Figure 1: Timbre suisse à l’effigie de Jacques Bernoulli.

Édité en 1994 à l’occasion du Congrès International des Mathématiciens, Zürich. Contexte. Alexandre-Théophile Vandermonde - Alexandre-Théophile Vandermonde - xcv.wiki. Alexandre-Théophile Vandermonde ( Paris , 28 février 1735 - ibid. , 1er janvier 1796) était un mathématicien, musicien et chimiste français qui travailla avec Bézout et Lavoisier ; son nom est maintenant principalement associé à la théorie des déterminants en mathématiques.

Biographie Vandermonde était violoniste, et ne s'est engagé dans les mathématiques que vers 1770. Matrice de Vandermonde. De façon matricielle, elle se présente ainsi : Autrement dit, pour tous i et j, Remarque.
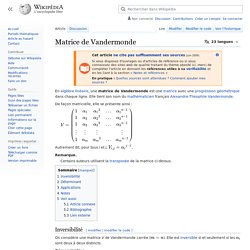
Certains auteurs utilisent la transposée de la matrice ci-dessus. Inversibilité[modifier | modifier le code] On considère une matrice V de Vandermonde carrée ( ). Sont deux à deux distincts. Démonstration Si deux coefficients sont identiques, la matrice a deux lignes identiques, donc n'est pas inversible.
Qui était Varignon? Dorothy Vaughan, mathématicienne visionnaire. Mathématicienne américaine, Dorothy Johnson Vaughan (1910 – 2008) a supervisé le groupe de scientifiques West Area Computers de la NASA, qui était alors la NACA.
Son histoire et celle de ses collègues ont été relatées dans le livre et le film Les Figures de l’ombre. Mathématicienne douée Fille d’Annie et de Leonard Johnson, Dorothy Vaughan nait le 20 septembre 1910 à Kansas City, dans le Missouri aux Etats-Unis. Elle y passe ses plus jeunes années avant de déménager avec sa famille à Morgantown, en Virginie-Occidentale. John Venn. Un article de Wikipédia, l'encyclopédie libre. signature Le Venn Building, université de Hull.

John Venn (1834-1923) est un mathématicien et logicien britannique, renommé pour avoir conçu les diagrammes de Venn qui sont employés dans beaucoup de domaines, notamment en théorie des ensembles, en probabilité, en logique, en statistique et en informatique. John Venn a présenté les diagrammes portant son nom en 1881. John Venn. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Fils d'un prêtre anglican, Venn reçoit une éducation chrétienne au sein d'établissements privés avant d'entreprendre des études de mathématiques et de philosophie à Cambridge (Gonville & Caius College).

Diplômé en 1857, ordonné prêtre en 1859, il obtient un poste de professeur de sciences morales à Cambridge (1862) tout en se vouant à la logique mathématique. John Venn fut élu membre de la Royal Society en 1883. ?!? Vous avez un doute quant au sens précis de sciences morales ? Tableaux et diagrammes de Venn. Deux (deux ?) minutes pour... Newroz. Mignonne, allons voir si Newroz... Ils l'ont fait !

La question était ouverte depuis les années 60, et pourtant, ils sont parvenus à le débusquer ! Les diagrammes de Venn symétriques et simples à 11 ensembles existent bel et bien ! Diagrammes d'Euler, de Venn et de Carroll. Un article de Wikipédia, l'encyclopédie libre. Les diagrammes d'Euler, de Venn et de Carroll sont des schémas géométriques utilisés pour représenter des relations logico-mathématiques.
Créés pour visualiser la structure logique des syllogismes, ils sont couramment utilisés pour l'étude des relations entre ensembles. Yves Colin de Verdière. Yves Colin de Verdière est un mathématicien français. Biographie et travaux[modifier | modifier le code] Il est connu pour ses travaux de géométrie spectrale, liés notamment au régime semi-classique de la mécanique quantique et au chaos quantique ; de théorie des graphes où il a introduit un nouvel invariant de nature spectrale (appelé l'invariant de Colin de Verdière)[1] ; et sur plusieurs autres sujets liés à la géométrie riemannienne et à la théorie des nombres.
Notes et références[modifier | modifier le code] Liens externes[modifier | modifier le code] Urbain Jean Joseph Le Verrier. UrbainLeVerrier Urbain Jean Joseph Le Verrier (Saint-Lô, 11 mars 1811 — Paris, 23 septembre 1877) était un astronome et mathématicien français spécialisé en mécanique céleste. Ses études Après huit ans d'études au collège de sa ville natale Saint-Lô, il entre au Collège Royal de Caen où il étudiera les mathématiques de 1827 à 1830. Il poursuit ses études au Collège Louis-le-Grand à Paris et est admis en 1831 à l'École polytechnique dont il sort deux ans après comme ingénieur des tabacs. Il travaillera d'abord au laboratoire de chimie de Gay-Lussac. Urbain Le Verrier. Urbain Le Verrier. Signature Urbain Le Verrier, né à Saint-Lô le 11 mars 1811, mort à Paris le 23 septembre 1877, est un astronome et mathématicien français spécialisé en mécanique céleste, découvreur de la planète Neptune et fondateur de la météorologie moderne française.
Ses études[modifier | modifier le code] Urbain Le Verrier devient membre de la section d'astronomie de l'Académie des sciences le 19 janvier 1846 et le 14 octobre de la même année membre-adjoint du Bureau des longitudes[4]. La découverte de Neptune[modifier | modifier le code] Urbain Jean Joseph LE VERRIER (1811-1877) Fils de Louis Baptiste LE VERRIER et de Marie Jeanne Joséphine Pauline de BAUDRE. Epoux de Marie Lucile Clotilde CHOQUET. Père de Louis Paul Urbain LE VERRIER (1848-1905 ; X 1867, corps des mines) et de Jean Charles Léon LE VERRIER (né en 1838 ; X 1856, corps des mines). Ancien élève de Polytechnique (promotion 1831, entré classé 4 et sorti classé 8 sur 121 élèves).
Antoine Yvon Villarceau. Les cercles de Villarceau sur le tore. Vinogradov Ivan Matveïevitch. Vitali Giuseppe. Le theoreme de Viviani. Vladimir Vapnik. Parle de Vladimir Vapnik: Qu’est-ce qui échappe à l’intelligence artificielle ? (9/11) Nouvelles méthodologies de la modélisation: Théorie de Vapnik et mise en oeuvre par KXEN.
Complete Statistical Theory of Learning (Vladimir Vapnik) Vladimir Vapnik: Predicates, Invariants, and the Essence of Intelligence. Viviani Vincenzo. TRIANGLE : THÉORÈME DE VIVIANI. Le théorème de Viviani - Automaths #16. Volterra Vito. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Après des études de physique à Florence, Volterra approfondit ses connaissances en mathématiques et physique à l'université de Pise (Pisa, Italie) où Betti fut son professeur. Il y enseignera la mécanique dès 1883.
En 1887, il publie à Rome un article fondateur : Sopra le funzioni che dipendono da altre funzioni (Sur les fonctions qui dépendant d'autres fonctions) pouvant être considéré comme l'acte de naissance de l'analyse fonctionnelle moderne (appellation de Paul Lévy, 1822). Il y définit le concept général d'opérateur, une généralisation de la notion de fonction dont le domaine de départ et d'arrivée ne sont plus des nombres mais des fonctions. Volterra consacra ses recherches et son enseignement à l'analyse fonctionnelle parallèlement à ceux du physicien et mathématicien suédois Fredholm. C'est quoi l'analyse fonctionnelle ? Morley Cole.
Mathématicien Vito Volterra. A l’origine du modèle appelé « proie-prédateur » il y a un grand mathématicien italien, Vito Volterra (1860-1940) et une histoire de poissons. Pendant la première guerre mondiale, Volterra fut très engagé comme militaire (malgré son âge) et comme directeur de « l’Ufficio Invenzioni e Ricerche ». Il fut l’un des mathématiciens italiens les plus actifs d’un point de vue scientifique et institutionnel : pendant les années 20, il fonda le « Consiglio Nazionale delle Ricerche » (CNR) (l’équivalent du CNRS français) avec la conviction que les mathématiques étaient de plus en plus indispensables aux autres sciences.
L’idée géniale de Volterra fut de distinguer les habitants de la mer en deux grandes catégories : les proies et les prédateurs, deux quantités variables en fonction du temps. En introduisant des hypothèses simplificatrices, Volterra trouva une formule qui lie la variation des proies à celle des prédateurs. Diagramme de Voronoï. Chronologie 1644 – René Descartes utilise de tels diagrammes pour représenter l'espace du système solaire. 1840 – Gauss observe le premier un rapport avec les formes quadratiques. Diagramme de Voronoi. Jouez avec les diagrammes de Voronoï.