

Découverte Junior Gérard Villemin Les courbes. Découverte Junior – Gérard Villemin Les courbes Par Clément en vacances sur la Côte d’Azur Le 15 Mars 2013 Géométrie Junior – Chapitre 10 1 Les droites Y Imaginons une voiture qui roule sur le bas de cette figure.
Elle pourrait s’appeler Ferrari ou Toto. On a décidé de l’appeler tout simplement X. En même temps une autre voiture, baptisée Y, monte le long du côté gauche. Parfois, la voiture Y va dix fois plus vite que la voiture X. 3 points de vue historiques sur les Courbes - Hors-Série. Aux frontières de la géométrie : un monde sans courbure. Index de courbes & fonctions remarquables. Voulez-vous tracer une courbe y = f(x) "on line" ?

Site de G. Valance, professeur de mathématiques. Famous Curves Index. Index et notations courbes planes. Voir les notations ci-dessous.
Courbes commençant par Classification par l'équation polaire : MATHCURVE.COM. Trièdre de Frenet et centre de courbure. La simulation trace le trajet d'un point M le long d'une courbe paramétrique plane.
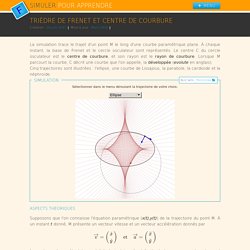
À chaque instant, la base de Frenet et le cercle osculateur sont représentés. Le centre C du cercle osculateur est le centre de courbure, et son rayon est le rayon de courbure. Lorsque M parcourt la courbe, C décrit une courbe que l'on appelle, la développée (evolute en anglais). Cinq trajectoires sont illustrées : l'ellipse, une courbe de Lissajous, la parabole, la cardioide et la néphroide. Simulation Built with Processing Sélectionner dans le menu déroulant la trajectoire de votre choix. Repère de Frénet (cinématique du point)
SUR LA DÉVIATION D’UNE COURBE PLANE. Géométrie des routes et virages. Famous Curves Index - MacTutor History of Mathematics. Index et notations courbes planes. Voir les notations ci-dessous.
Courbes commençant par Classification par l'équation polaire : Classification par l'équation cartésienne explicite en y (courbes algébriques) : Classification par la forme : Définitions géométriques à partir de deux pôles A et B. Les courbes de degré au plus 2. Retour à la page personnelle de Bernard Parisse.

Ce sont les courbes qui ont comme équation, dans un repère Oxy, P(x,y)=0 où P est un polynôme de degré inférieur ou égal à 2. 16.1 La droite. Abscisse curviligne. Nos et nous-mêmes stockons et/ou accédons à des informations stockées sur un terminal, telles que les cookies, et traitons les données personnelles, telles que les identifiants uniques et les informations standards envoyées par chaque terminal pour diffuser des publicités et du contenu personnalisés, mesurer les performances des publicités et du contenu, obtenir des données d'audience, et développer et améliorer les produits.
Avec votre permission, nos partenaires et nous-mêmes pouvons utiliser des données de géolocalisation précises et d’identification par analyse du terminal. En cliquant, vous pouvez consentir aux traitements décrits précédemment. Vous pouvez également accéder à des informations plus détaillées et modifier vos préférences avant de consentir ou pour refuser de donner votre consentement. Veuillez noter que certains traitements de vos données personnelles peuvent ne pas nécessiter votre consentement, mais vous avez le droit de vous y opposer.
La longueur d'un arc de la courbe représentative d'une fonction (vidéo) Prof de meca-longueur de l'astroide - abscisse curviligne.
Courbes de Bézier. LA CATOPTRICE : UNE COURBE PRESQUE OUBLIÉE. Le 26 août 2012 - Ecrit par Hamza Khelif Lire l'article en On appelle catoptrice (du Grec - miroir) [1] une courbe C qui jouit de la propriété qu’il existe un point F intérieur à C tel que si un rayon de lumière passant par ce point est réfléchi en M puis en N sur cette courbe alors ce rayon passe de nouveau par F.

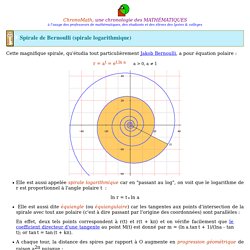
Le problème de la détermination des catoptrices, posé par Euler en 1745 dans Nova Acta Eruditorum, est peut-être le plus intéressant parmi une collection de problèmes étudiés surtout par Euler et probablement nommés par lui « Problèmes réciproques » [2]. Les ellipses, vu leur propriété optique [3], sont des catoptrices (relativement à un foyer) (fig.1), mais Euler voulait connaitre toutes les autres. Il ne laisse pas beaucoup de temps à ses collègues pour travailler sur ce problème puisque l’année suivante et dans le même journal, il présente sa « Solution au problème de la catoptrice ». Référence. Brachistochrone et chaînette. Etude de la quadrature de la spirale d’Archimède (Daena Paloma) Maths: spirale logarithmique. Spirale logarithmique. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Cette magnifique spirale a pour équation polaire : r = at = et.ln a a > 0, a ≠ 1 Elle est aussi appelée spirale logarithmique car en "passant au log", on voit que le logarithme de r est proportionnel à l'angle polaire t :
Kurven. 2012 CuisinierGuissard Engrenages Losanges18 md. Spirograph. The name has been a registered trademark of Hasbro Inc. since 1998 following purchase of the company that had acquired the Denys Fisher company.
The Spirograph brand was relaunched worldwide in 2013, with its original product configurations, by Kahootz Toys. Epicycloïdes. CardioÏdes. Hypocycloïde. Deltoïde. Epicycloïdes - Caustiques. Courbes planes. Propriétés métriques des courbes planes.
91b. Tractrice. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Ce problème rappelle les anciens chemins de halage où des chevaux, en se déplaçant le long des canaux, tiraient des embarcations, d'où son nom. Cette courbe fut étudiée par Isaac Newton (1676) et par le mathématicien et physicien hollandais Christian Huygens sous le nom de tractoria. Considérons un point "pesant" T (comme disent les physiciens), tiré en M au bout d'un fil de longueur a. M se déplaçant linéairement : Courbes gauches.
ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Une parabole, une sinusoïde sont des courbes planes. Une ellipse, un cercle sont des courbes planes fermées. Pour ces exemples, tous les points des courbes considérées sont situés dans un même plan : une courbe est dite gauche (gauchir = dévier, tordre) s'il n'en est pas ainsi. C'est une courbe dans l'espace euclidien usuel à trois dimensions dont un des premiers grands spécialistes français fut Alexis Clairaut. Un exemple simple de courbe gauche est donné par un ressort, la vrille d'un tire-bouchon, la forme de l'escalier en colimaçon d'une tour (en hélice). Jacques Bernoulli. Pour échapper aux persécutions religieuses menées par les Espagnols aux Pays-Bas, la famille Bernoulli quitte Anvers en 1583 pour se réfugier à Francfort et s’établir définitivement à Bâle en Suisse en 1622.
Parmi les descendants, il y aura huit mathématiciens de talent sur trois générations, dont les plus célèbres sont les frères Jacques et Jean, qui sont également les deux premiers mathématiciens de la lignée, et leur neveu Daniel. Jacques Bernoulli est né à Bâle le 27 décembre 1654 et y est mort le 16 août 1705. Pour répondre aux attentes de son père, Jacques Bernoulli a d’abord étudié la théologie. Cependant, il ne put résister longtemps à son intérêt pour les disciplines scientifiques. À partir des travaux de Wallis, de Barrow et des articles de Leibniz publiés en 1684 et 1687 dans les Acta Eruditorum, il a assimilé par lui-même le calcul différentiel et intégral.
MEDIA180913160504721. Atelier L34. From Wolfram MathWorld. A toric section is a curve obtained by slicing a torus (generally a horn torus) with a plane. A spiric section is a special case of a toric section in which the slicing plane is perpendicular to both the midplane of the torus and to the plane Consider a torus with tube radius . Des courbes marrantes. Des courbes marrantes fin. [Conférence] E. GHYS - La coupe des pierres, une source de théorèmes mathématiques. Courbes algébriques. Courbes gauches.
Indicatrice de Dupin. INDICATRICE DE DUPINDupin's indicatrix, Dupinsche Indikatrix Lorsqu’un plan parallèle au plan tangent en un point M d’une surface tend vers celui-ci, sa section avec la surface tend à devenir homothétique d’une courbe qui, normalisée convenablement, est l’indicatrice de Dupin du point de cette surface.Lorsque le point n’est pas un méplat, l’indicatrice de Dupin est la réunion de deux coniques, d'équation dans le plan tangent rapporté aux directions principales, où R1 et R2 sont les rayons de courbure principaux de la surface en M. Ces directions principales sont données par les deux lignes de courbure passant par le point. © Robert FERRÉOL 2003.
Développée. Un article de Wikipédia, l'encyclopédie libre. On suppose la courbe suffisamment dérivable et birégulière. Si elle est paramétrée par l'abscisse curviligne sous la forme , le centre de courbure s'obtient en posant où est le centre de courbure, Développée d'une courbe. DÉVELOPPÉE D'UNE COURBEEvolute of a curve, Evolute einer Kurve. Développante d'une surface développable. DÉVELOPPANTE D'UNE COURBE, D'UNE SURFACE DÉVELOPPABLEInvolute of a curve, of a developable surface, Evolvente einer Kurve, einer Torse. DES CARTES, DES GOSSES ET DES BONNETS.
Un ellipsoïde peut en cacher un autre. Ellipsoïde. Au delà du compas : la géométrie des courbes. Courbes paramétrées. Le dictionnaire entre l'algèbre et la géométrie (le Nullstellensatz) MULTIPLIER OU DIVISER PAR L’ABSCISSE, À LA MAIN ! Le 19 septembre 2010 - Ecrit par Pierre Lecomte En appliquant une transformation simple à effectuer point par point avec une règle graduée, on peut facilement construire le graphe de , ou de , à partir de celui de . La multiplication par l’abscisse est décrite sur la figure suivante, suffisamment explicite me semble-t-il pour ne pas devoir préciser davantage les choses :
Courbe du chien = courbe de poursuite. Courbes Iso...truc (iso=même) Pascal, Roberval et la quadrature de la cycloïde (Thierry Lambre) PYTHAGORE ET LES COURBES DE PÓLYA. Le théorème de Pythagore est enseigné dans les collèges français. Ces courbes qui colorient tout l'espace. Interpolation polynomiale. Trajectoire de l'arbitre au foot et plusieurs tortues. Courbe Batman. Index et notations courbes planes. Voir les notations ci-dessous. UNE VERSION SIMPLIFIÉE DU THÉORÈME DE GAUSS-BONNET. Le théorème de Gauss-Bonnet. Courbure. Rayon de courbure. Courbe de Joukowski. Mathématiques avec Python et Ruby/Joukovski et Ruby — Wikilivres. Nikolay Yegorovich Joukovski. Courbes ornementales. Fleur.
Chaînette, tractrice et brachistochrone. Courbes, surfaces... Voyage au bout du tore. Courbes et surfaces paramétrées. Rédactions de recherche. Etude de la quadrature de la spirale d’Archimède (Daena Paloma) LES COURBES EN CRÉNEAUX. Article courbe Thierry Joffredo définitif 2020. LE LOGO DU CNRS. À propos d’une œuvre de Kupka. IFT 3355 Infographie Courbes et surfaces Victor Ostromoukhov. Enveloppe convexe d'une famille de courbes. Courbes et Surfaces. Tracés de maçonnerie. Voutes. SURFACES À COURBURE MOYENNE CONSTANTE.
Isopérimétrie. Courbes auto-similaires remplissant l'espace de pentagones réguliers, d'heptagones et d'autres n-gons (anglais) L'aiguille de Kakeya. R. Mansuy - Maths Monde 2020 - Le problème de Kakeya - Serveur vidéo de l'IREM de Paris.