

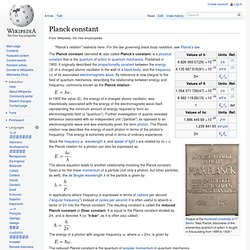
Planck constant. Plaque at the Humboldt University of Berlin: "Max Planck, discoverer of the elementary quantum of action h, taught in this building from 1889 to 1928.
" In 1905 the value (E), the energy of a charged atomic oscillator, was theoretically associated with the energy of the electromagnetic wave itself, representing the minimum amount of energy required to form an electromagnetic field (a "quantum"). Further investigation of quanta revealed behaviour associated with an independent unit ("particle") as opposed to an electromagnetic wave and was eventually given the term photon. The Planck relation now describes the energy of each photon in terms of the photon's frequency. This energy is extremely small in terms of ordinary experience. Quantum mechanics. Wavefunctions of the electron in a hydrogen atom at different energy levels.
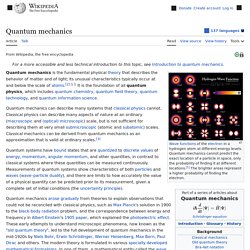
Quantum mechanics cannot predict the exact location of a particle in space, only the probability of finding it at different locations.[1] The brighter areas represent a higher probability of finding the electron. Quantum mechanics (QM; also known as quantum physics, quantum theory, the wave mechanical model, or matrix mechanics), including quantum field theory, is a fundamental theory in physics which describes nature at the smallest scales of atoms and subatomic particles.[2] Quantum mechanics gradually arose from theories to explain observations which could not be reconciled with classical physics, such as Max Planck's solution in 1900 to the black-body radiation problem, and from the correspondence between energy and frequency in Albert Einstein's 1905 paper which explained the photoelectric effect.
History[edit] In 1838, Michael Faraday discovered cathode rays. Where h is Planck's constant. Coulomb potential. Axiom. An axiom or postulate is a premise or starting point of reasoning.
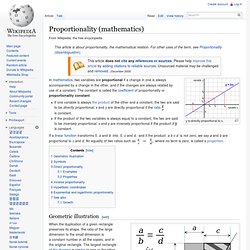
As classically conceived, an axiom is a premise so evident as to be accepted as true without controversy.[1] The word comes from the Greek axíōma (ἀξίωμα) 'that which is thought worthy or fit' or 'that which commends itself as evident.'[2][3] As used in modern logic, an axiom is simply a premise or starting point for reasoning.[4] Axioms define and delimit the realm of analysis; the relative truth of an axiom is taken for granted within the particular domain of analysis, and serves as a starting point for deducing and inferring other relative truths. Proportionality (mathematics) Y is directly proportional to x.
Linear function. In mathematics, the term linear function refers to two different, although related, notions:[1] As a polynomial function[edit] In calculus, analytic geometry and related areas, a linear function is a polynomial of degree one or less, including the zero polynomial (the latter not being considered to have degree zero).
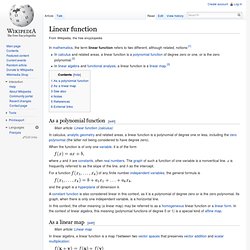
For a function. Polynomial. The graph of a polynomial function of degree 3 Etymology[edit] According to the Oxford English Dictionary, polynomial succeeded the term binomial, and was made simply by replacing the Latin root bi- with the Greek poly-, which comes from the Greek word for many.
Algebra. "Algebraist" redirects here.
For the novel by Iain M. Pure mathematics. Mathematical formulæ Broadly speaking, pure mathematics is mathematics that studies entirely abstract concepts.
From the eighteenth century onwards, this was a recognized category of mathematical activity, sometimes characterized as speculative mathematics,[1] and at variance with the trend towards meeting the needs of navigation, astronomy, physics, economics, engineering, and so on. Another insightful view put forth is that pure mathematics is not necessarily applied mathematics: it is possible to study abstract entities with respect to their intrinsic nature, and not be concerned with how they manifest in the real world.[2] Even though the pure and applied viewpoints are distinct philosophical positions, in practice there is much overlap in the activity of pure and applied mathematicians. To develop accurate models for describing the real world, many applied mathematicians draw on tools and techniques that are often considered to be "pure" mathematics.
History[edit] 19th century[edit] Ring (mathematics) Chapter IX of David Hilbert's Die Theorie der algebraischen Zahlkörper.
The chapter title is Die Zahlringe des Körpers, literally "the number rings of the field". The word "ring" is the contraction of "Zahlring". Rings were first formalized as a common generalization of Dedekind domains that occur in number theory, and of polynomial rings and rings of invariants that occur in algebraic geometry and invariant theory. They are also used in other branches of mathematics such as geometry and mathematical analysis. Field (mathematics) Commutative rings ⊃ integral domains ⊃ integrally closed domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields ⊃ finite fields.
Intuitively, a field is a set F that is a commutative group with respect to two compatible operations, addition and multiplication, with "compatible" being formalized by distributivity, and the caveat that the additive identity (0) has no multiplicative inverse (one cannot divide by 0). Closure of F under addition and multiplication For all a, b in F, both a + b and a · b are in F (or more formally, + and · are binary operations on F). Binomial. Monomial. Scale of the Universe 2.