

Forms Matter. This story was co-published with ProPublica. Forms. They’re the often-tedious tasks that stand in the way of an online purchase, seeing the doctor, or filing your taxes. They may be boring, but they have tremendous power. Whether you’re filling out a form or building it yourself, you should be aware that decisions about how to design a form have all kinds of hidden consequences.
How you ask a question, the order of questions, the wording and format of the questions, even whether a question is included at all—all affect the final result. How You Ask the Question: The Census The Census determines everything from how our congressional districts are drawn to how $400 billion in federal aid is distributed to enforcement of civil rights laws.
But even small changes in the ways Census forms ask questions can have surprising effects, and not just because of the inherent limitations of asking people to put their identity in a box. The Census Race and Hispanic Origin Question in 1990 and 2000. Version 1.1 of the likert Package Released to CRAN. Categorized as: R, R-Bloggers After some delay, we are happy to finally get version 1.1 of the likert package on CRAN.

Although labeled 1.1, this is actually the first version of the package released to CRAN. After receiving some wonderful feedback from useR! This year, we held back releasing until we implemented many of the feature suggestions. The NEWS file details most of what is in this release, but here are some highlights: Simplify analyzing and visualizing Likert type items using R’s familiar print, summary, and plot functions. Oh Ordinal data, what do we do with you? Common Approaches for Analyzing Likert Scales and Other Categorical Data. Analyzing Likert scale responses really comes down to what you want to accomplish (e.g.
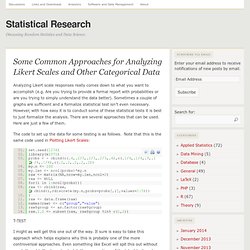
Are you trying to provide a formal report with probabilities or are you trying to simply understand the data better). Sometimes a couple of graphs are sufficient and a formalize statistical test isn’t even necessary. Which hypothesis test for Likert scale? Drinking, sex, eating: Why don't we tell the truth in surveys? 27 February 2013Last updated at 13:56 GMT By Brian Wheeler BBC News Magazine.
Video: Survey Package in R. Sebastián Duchêne presented a talk at Melbourne R Users on 20th February 2013 on the Survey Package in R.
Talk Overview: Complex designs are common in survey data. In practice, collecting random samples from a populations is costly and impractical. Therefore the data are often non-independent or disproportionately sampled, and violate the typical assumption of independent and identically distributed samples (IDD). The Survey package in R (written by Thomas Lumley) is a powerful tool that incorporates survey designs to the data. Standard statistics, from linear models to survival analysis, are implemented with the corresponding mathematical corrections. About the presenter: Sebastián Duchêne is a Ph.D. candidate at The University of Sydney, based at the Molecular Phylogenetics, Ecology, and Evolution Lab. Asdfree by anthony damico. How I can prevent and treat missing data for questionnaires. Sample Size: How Many Survey Participants Do I Need?
Please ensure you have JavaScript enabled in your browser.
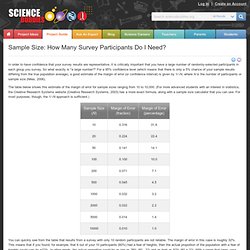
If you leave JavaScript disabled, you will only access a portion of the content we are providing. <a href="/science-fair-projects/javascript_help.php">Here's how. </a> How Many Subjects Do I Need for a Statistically Valid Survey? By Daryle Gardner-Bonneau, Ph.D.

Office of Research Michigan State University/Kalamazoo Center for Medical Studies Reprinted from Usability Interface, Vol 5, No. 1, July 1998. An intro to power and sample size estimation. + Author Affiliations Correspondence to: Dr S R Jones, Emergency Department, Manchester Royal Infirmary, Oxford Road, Manchester M13 9WL, UK; steve.r.jones@bigfoot.com Abstract The importance of power and sample size estimation for study design and analysis.
What is a large enough random sample? With the well deserved popularity of A/B testing computer scientists are finally becoming practicing statisticians.
One part of experiment design that has always been particularly hard to teach is how to pick the size of your sample. The two points that are hard to communicate are that: The required sample size is essentially independent of the total population size.The required sample size depends strongly on the strength of the effect you are trying to measure. These things are only hard to explain because the literature is overly technical (too many buzzwords and too many irrelevant concerns) and these misapprehensions can’t be relieved unless you spend some time addressing the legitimate underlying concerns they are standing in for. As usual explanation requires common ground (moving to shared assumptions) not mere technical bullying. From Power Calculations to P-Values: A/B Testing at Stack Overflow.
Note: cross-posted with the Stack Overflow blog.

Binary sample size calculator. Binary outcomes Suppose you want to test whether more people respond to one drug versus another, or whether one advertising campaign is more effective than another.

In either case, you have a binary outcome. Someone either responds to the drug or they don’t. They either buy the product or they don’t. In either case you have a probability of something happening, p1 for one group and p2 for the other, and you would like to test whether the two probabilities are different enough to tell apart, i.e. that their difference is statistically significant. The answer depends on many factors. Sample size calculator The calculator below will estimate n, the number of subjects you need to assign to each group, based on your initial guesses at p1 and p2 and some common assumptions.
Sample size / power calculation for logrank survival test.