Mathematics. Vous êtes sur le blog de David Madore, qui, comme le reste de ce site web, parle de tout et de n'importe quoi (surtout de n'importe quoi, en fait), des maths à la moto et ma vie quotidienne, en passant par les langues, la politique, la philo de comptoir, la géographie, et beaucoup de râleries sur le fait que les ordinateurs ne marchent pas, ainsi que d'occasionnels rappels du fait que je préfère les garçons, et des petites fictions volontairement fragmentaires que je publie sous le nom collectif de fragments littéraires gratuits. • Ce blog eut été bilingue à ses débuts (certaines entrées étaient en anglais, d'autres en français, et quelques unes traduites dans les deux langues) ; il est maintenant presque exclusivement en français, mais je ne m'interdis pas d'écrire en anglais à l'occasion. • Pour naviguer, sachez que les entrées sont listées par ordre chronologique inverse (i.e., celle écrite en dernier est en haut).
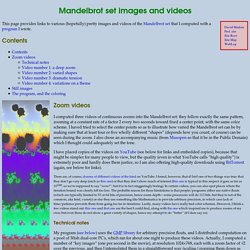
(RSS 1.0) • Recent comments / Commentaires récents] terme formule. Mandelbrot set images and videos. This page provides links to various (hopefully) pretty images and videos of the Mandelbrot set that I computed with a program I wrote. Contents Zoom videos I computed three videos of continuous zooms into the Mandelbrot set: they follow exactly the same pattern, zooming at a constant rate of a factor 2 every two seconds toward fixed a center point, with the same color scheme. I haved tried to select the center points so as to illustrate how varied the Mandelbrot set can be by making sure that at least four or five wholly different “shapes” (depends how you count, of course) can be seen during the zoom. There are, of course, dozens of different videos of the kind on YouTube. Technical notes My program (see below) uses the GMP library for arbitrary precision floats, and I distributed computation on a pool of 30ish dual-core PC's, which ran for about one night to produce these videos.
Video number 1: a deep zoom Video number 2: varied shapes The second video is 3′09″ long. Still images. Geometrie plane -- geometrie projective. Comme promis, je vais tenter, en une série de posts dans ce blog, de faire un peu de vulgarisation de la géométrie plane, et je commence par parler de la géométrie projective. Alors, qu'est-ce que c'est que la géométrie projective ?
C'est un terme qui fait souvent peur (par exemple à mes agrégatifs ), et je n'arrive pas à comprendre pourquoi : la géométrie projective, au contraire, c'est la plus simple qui soit, parce qu'il n'y est question ni d'angles ni de distances, ni même de droites parallèles, mais uniquement de droites qui se rencontrent et de points alignés. La géométrie projective, donc, c'est celle que vous faites si vous avez pour seul instrument une règle non graduée (et un papier et un crayon, d'accord) : vous pouvez relier deux points par une droite, vous pouvez trouver le point d'intersection de deux droites, mais vous ne pouvez rien faire d'autre. Cela semble très facile ? Pourtant, on entre déjà dans un monde assez riche. point à l'infini droite à l'infini . Dual. The Cubic Surfaces DVD. What is this? The Cubic Surfaces DVD is a series of computer-generated animations (54 in total) displaying cubic surfaces and deformations thereof. It was created to help better visualize what cubic surfaces look like and what their singular points can be: it tries to be of both mathematical interest and artistic value.
The DVD ISO image is available for download from this page, and the individual animations can also be downloaded separately. For some mathematical generalities about cubic surfaces, please consult this historical article, this MathWorld article and this Wikipedia article. (Of course, you don't need to know any mathematics just to watch the animations!) The DVD animations were computed using the Persistence of Vision raytracer (on a PC runing the Debian GNU/Linux operating system). The entire contents of the DVD and its source code and related material (including this Web page) are placed in the Public Domain by the author (David A. The DVD Downloading it Burning it Buying it. The On-Line Encyclopedia of Integer Sequences™ (OEIS™)