

Fractals. Fractals Dans cette image, des milliards de mondes...

Ensemble de mandelbrot. Dans l'ensemble des nombres complexes, on considère la suite : Les différentes images z1, z2, ... sont bornées lorsque c = z1 est dans M et dans ce cas seulement.

Forme fractale aux propriétés fascinantes, cet ensemble M fut tracé pour la première fois en 1980 par Benoît Mandelbrot à l'aide d'un micro-ordinateur. Une deuxième animation. Mandelbrot set images and videos. This page provides links to various (hopefully) pretty images and videos of the Mandelbrot set that I computed with a program I wrote.
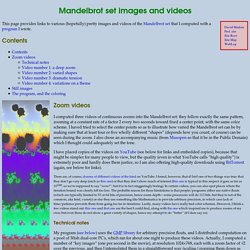
Contents Zoom videos I computed three videos of continuous zooms into the Mandelbrot set: they follow exactly the same pattern, zooming at a constant rate of a factor 2 every two seconds toward fixed a center point, with the same color scheme. I haved tried to select the center points so as to illustrate how varied the Mandelbrot set can be by making sure that at least four or five wholly different “shapes” (depends how you count, of course) can be seen during the zoom. I also chose an accompanying music (from Musopen so that it be in the Public Domain) which I thought could adequately set the tone. There are, of course, dozens of different videos of the kind on YouTube. Technical notes Video number 1: a deep zoom The first video (of which the image on the right is a sample) is 4′14″ long (actually 4′12″ on YouTube because it lacks the final fadeout).
Arithm'Antique n°8 - Les fractales. Fractal Geometry - MacTutor History of Mathematics. Any mathematical concept now well-known to school children has gone through decades, if not centuries of refinement.

A typical student will, at various points in her mathematical career -- however long or brief that may be -- encounter the concepts of dimension, complex numbers, and "geometry". If the field of mathematics does not particularly interest her, this student might see these concepts as distinct and unrelated and, in particular, she might make the mistake of thinking that the Euclidean geometry taught to her in school encompasses the whole of the field of geometry.
However, if she were to pursue mathematics at the university level, she might discover an exciting and relatively new field of study that links the aforementioned ideas in addition to many others: fractal geometry. While the lion's share of the credit for the development of fractal geometry goes to Benoît Mandelbrot, many other mathematicians in the century preceding him had laid the foundations for his work. IV Fractale. Rémi Carles - Dimensions bizarres. Deux (deux ?) minutes pour Mandelbrot. Fractales. FRACTAL MICHEL Accueil. Galery. Une galerie d'objets fractals et mathématiques. IFS, fractales et jeu du chaos. Y.

Morel Des images et des fractales Avant de s'attaquer aux principes, mathématiques et autres algorithmes, sur les IFS, attracteurs et jeu du chaos, quelques images / liens pour voir de quoi il s'agit. Ensembles de Julia - Experimentarium Digitale. Experimentarium Digitale Expérimentation Numérique Interactive et grains logiciels 3.0 Since … 1992 ;-)
Patterns. Symmetries. Rational maps with symmetries The group of automorphisms Aut(f) of a rational map f:P1->P1 of degree d>1 is defined to be the group of Moebius transformations that commute with that rational map.

When Aut(f) is not trivial, we say that f is a rational map with symmetries. The group Aut(f) is a finite subgroup of PSL(2,C). Polynomial matings. Here you will find movies of polynomial matings on the Riemann sphere.

Polynomial mating is the name given by Douady an Hubbard to a phenomenon that they discovered: the Julia sets of some rational maps is homeomorphic to the gluing of two filled-in polynomial Julia sets along their boundaries, by a gluing that respects the marking by external angle and thus the corresponding dynamical systems on the Julia sets. A progressive interpolation was introduced, between the two polynomial Julia sets and their mating. It consists in gluing equipotentials together and gives a holomorphic dynamical system between different spheres (this was observed by Milnor). This dynamical systems gives an easy method for drawing a conformally correct picture of the deformation of the polynomial Julia sets under the equipotential gluing: this method was explained to me by Buff.
The result is an image which depends on the potential. Math Park - 07/02/15 - Xavier Buff, Où sont les zéros des polynômes ? FractalsUToronto1. FractalsUToronto11. FractalsUToronto12. Introduction to Fractal Geometry and Chaos Theory. Winter 2020: University of Toronto, BA6180, Monday 5-6pm and Tuesday 10am-noon Instructor: Matilde Marcolli Brief Course Description The course will give an introduction to fractal geometry and chaotic dynamics, with an emphasis on geometric aspects.
Topics covered will include various notions of fractal dimensions, fractal measures, symbolic dynamics, notions of entropy, chaos in dynamical systems and strange attractors, geometric operators (Laplacians, Dirac, etc.) on fractal objects. The course will be suitable also for students from other departments interested in applications of fractals and chaos. ANNOUNCEMENT (March 13): Due to new directives from the university, we have to suspend in-person classes. Animations. Home Page. Fractales à la recherche de la dimension cachée HD part 1/4. Fractales à la recherche de la dimension cachée HD part 2/4. Fractales à la recherche de la dimension cachée HD part 3/4. Fractales à la recherche de la dimension cachée HD part 4/4. Images des mathématiques.
Piste verte Le 26 juillet 2016 - Ecrit par Jos Leys Les ensembles de Julia sont parmi les exemples les plus célèbres d’ensembles fractals.

On se fixe un nombre complexe et on considère alors l’ensemble des points du plan complexe qui ne partent pas vers l’infini sous l’action répétée de la transformation . Rediffusion d’un article du 17 juin 2013. Pour en savoir plus, voir cet article. En ajoutant une profondeur à la zone en dehors de l’ensemble on crée des montagnes, comme dans ce film : Par Michèle Audin et Arnaud Chéritat: les ensembles limites. Au cours d’une étude historique des travaux de Fatou et Julia sur l’itération des fractions rationnelles, l’une des auteurs de cet article (que nous désignerons par la lettre M, nous utiliserons la lettre A pour désigner l’autre auteur) s’intéresse à l’histoire des images, images d’« ensembles de Julia » notamment.
Mathematical imagery by Jos Leys. Hybrid 3D fractals. 3D Kleinian escape time. Fractales "algorithmiques"