

The Pythagorean Theorem and its many proofs. The Pythagorean Theorem and its many proofs Pythagorean Theorem In a right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs. a² + b² = c² There are several methods to prove the Pythagorean Theorem.
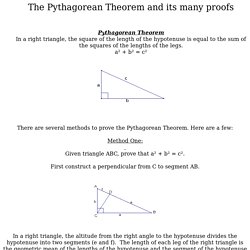
Here are a few: Method One: Given triangle ABC, prove that a² + b² = c². Self-exponential function. Untitled. Nov 2001 The paradoxes of the philosopher Zeno, born approximately 490 BC in southern Italy, have puzzled mathematicians, scientists and philosophers for millennia.

Although none of his work survives today, over 40 paradoxes are attributed to him which appeared in a book he wrote as a defense of the philosophies of his teacher Parmenides. Parmenides believed in monism, that reality was a single, constant, unchanging thing that he called 'Being'. In defending this radical belief, Zeno fashioned 40 arguments to show that change (motion) and plurality are impossible. 2D-3D. Well done Daniel Tuck for your solution and also Tony Cardell, age 14, State College Area High School, Pennsylvania, USA The first part requires only some very elementary geometry and knowledge of how to work out the area of circles and triangles.
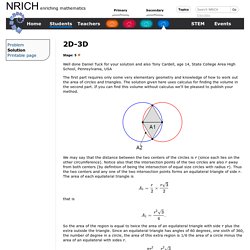
The solution given here uses calculus for finding the volume in the second part. My life: reading, movies and mathematics. Math diagrams. Exterior algebra. Orientation defined by an ordered set of vectors.
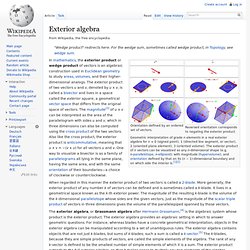
Reversed orientation corresponds to negating the exterior product. The exterior algebra, or Grassmann algebra after Hermann Grassmann,[4] is the algebraic system whose product is the exterior product. The exterior algebra provides an algebraic setting in which to answer geometric questions. For instance, whereas blades have a concrete geometrical interpretation, objects in the exterior algebra can be manipulated according to a set of unambiguous rules. Differentiating power series. I’m writing this post as a way of preparing for a lecture.

I want to discuss the result that a power series is differentiable inside its circle of convergence, and the derivative is given by the obvious formula . Tim Greer's Home Page. Greetings.
See my page introduction if you are interested. The prettiest pictures here are my favorite fractal creations. (The fractal animations are no longer available through this site.) Full mathematical details are available through the links below. Jonathan Manton's Blog. The previous lecture looked at some of the lower-level details of affine spaces.
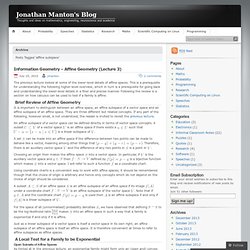
This is a prerequisite for understanding the following higher-level overview, which in turn is a prerequisite for going back and understanding the lower-level details in a finer and precise manner. Following the review is a section on how calculus can be used to test if a family is affine. Brief Review of Affine Geometry It is important to distinguish between an affine space, an affine subspace of a vector space and an affine subspace of an affine space.
They are three different but related concepts. Calculus III. Show Mobile NoticeShow All NotesHide All Notes You appear to be on a device with a "narrow" screen width (i.e. you are probably on a mobile phone).

Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in landscape mode many of the equations will run off the side of your device (should be able to scroll to see them) and some of the menu items will be cut off due to the narrow screen width. Here are my online notes for my Calculus III course that I teach here at Lamar University. Despite the fact that these are my “class notes”, they should be accessible to anyone wanting to learn Calculus III or needing a refresher in some of the topics from the class. These notes do assume that the reader has a good working knowledge of Calculus I topics including limits, derivatives and integration. Fractals optimization. 4404-Notes-ITM. Prob11. Integrale delta di Dirac. Spezzo il post in due, poichè è abbastanza lungo. nico88desmo ha scritto:Poi, perchè è sbagliato mettere il "d"t?
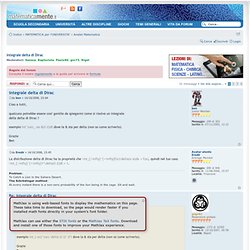
Come detto da Gugo82, sto frequentando ingegneria; ciò nonostante mi interessa capire dov'è l'errore concettuale in questo caso: magari se è possibile spiegarlo con termini semplici chiedo troppo? Il "d"t (o "d"x o altro fattore differenziale contenente una o più variabili) non è che sta sotto il segno d'integrale solo "per bellezza" o per indicare rispetto a quale variabile si integra; il "d"t ha un significato matematicamente più profondo, che cerco di sintetizzare.
Tra la fine dell' '800 e l'inizio del '900 i matematici si sono resi conto che l'integrale di Riemann non era troppo "buono": infatti, come hai visto o vedrai in Analisi II, i teoremi di passaggio al limite sotto il segno d'integrale hanno ipotesi "ingombranti", poiché richiedono convergenze troppo forti (di tipo uniforme). (*) \quad \int_E f " d"\mu \quad, \int_(-oo)^(+oo) f " d"\delta_(t_0) \quad. E-Learning per il Corso di Laurea in Matematica. The philosophy of mathematics. Introduction There is a philosophical doctrine known as bialetheism, with, apparently, many adherents in Australia, who take the view that there can be true contradictions.

I do not wish to defend this view, but nevertheless in the next 45 minutes I will be arguing, sincerely, that mathematics both does and does not need a philosophy. Of course, the apparent contradiction can in my case be resolved in a boringly conventional way: the statement "Mathematics needs philosophy" has at least two reasonable interpretations, and my contention is that one of them is false and another is true. But before I tell you what these interpretations are, I would like to say just a bit about what I hope to achieve in this talk, since as the first speaker in the series I have no precedents to draw on and have therefore had to decide for myself what kind of talk would be appropriate. First, as you can see, I am reading from a script, something I would never do when giving a mathematics lecture. 1. S: Yes.