

Épistémologie cognitive. Heuristics. Métaheuristique - Wiki. Un article de Wikipédia, l'encyclopédie libre.
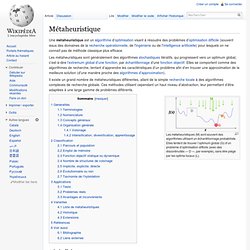
Il existe un grand nombre de métaheuristiques différentes, allant de la simple recherche locale à des algorithmes complexes de recherche globale. Ces méthodes utilisent cependant un haut niveau d’abstraction, leur permettant d’être adaptées à une large gamme de problèmes différents. Les métaheuristiques (M) sont souvent des algorithmes utilisant un échantillonnage probabiliste. Elles tentent de trouver l’optimum global (G) d’un problème d’optimisation difficile (avec des discontinuités — D —, par exemple), sans être piégé par les optima locaux (L). Généralités[modifier | modifier le code] Terminologies[modifier | modifier le code] On parle de méta, du grec μετά « au-delà » (comprendre ici « à un plus haut niveau »), heuristique, du grec εὑρίσκειν / heuriskein, qui signifie « trouver ». Heuristique.
Un article de Wikipédia, l'encyclopédie libre.
Cette page d’homonymie répertorie les différents sujets et articles partageant un même nom. Sur les autres projets Wikimedia : heuristique, sur le Wiktionnaire L'heuristique (du grec ancien εὑρίσκω, eurisko, « je trouve »[1]), parfois orthographiée euristique, est un terme de didactique qui signifie « l'art d'inventer, de faire des découvertes »[2]. Loi de Poisson. Un article de Wikipédia, l'encyclopédie libre.
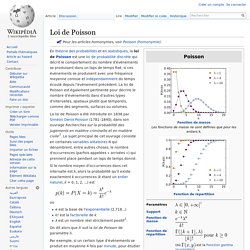
La loi de Poisson a été introduite en 1838 par Siméon Denis Poisson (1781–1840), dans son ouvrage Recherches sur la probabilité des jugements en matière criminelle et en matière civile[2]. Le sujet principal de cet ouvrage consiste en certaines variables aléatoires N qui dénombrent, entre autres choses, le nombre d'occurrences (parfois appelées « arrivées ») qui prennent place pendant un laps de temps donné.
Si le nombre moyen d'occurrences dans cet intervalle est λ, alors la probabilité qu'il existe exactement k occurrences (k étant un entier naturel, k = 0, 1, 2, ...) est où e est la base de l'exponentielle (2,718...)k! On dit alors que X suit la loi de Poisson de paramètre λ. Calcul de p(k)[modifier | modifier le code] Ce calcul peut se faire de manière déductive en travaillant sur une loi binomiale de paramètres (T; λ/T). Il peut aussi se faire de manière inductive en étudiant sur l'intervalle [0; T] les fonctions On note Remarques : et.
Probabilité. Un article de Wikipédia, l'encyclopédie libre.
La probabilité d'un événement est un nombre réel compris entre 0 et 1. Plus ce nombre est grand, plus le risque, ou la chance, que l'événement se produise est grand. L'étude scientifique des probabilités est relativement récente dans l'histoire des mathématiques. L'étude des probabilités a connu de nombreux développements depuis le XVIIIe siècle grâce à l'étude de l'aspect aléatoire et en partie imprévisible de certains phénomènes, en particulier les jeux de hasard. Ceux-ci ont conduit les mathématiciens à développer une théorie qui a ensuite eu des implications dans des domaines aussi variés que la météorologie, la finance ou la chimie. Historique[modifier | modifier le code] Au XVIIIe siècle, Gabriel Cramer donne un cours sur la logique probabiliste qui deviendra une base à l'article probabilité de l'encyclopédie de Diderot écrite à la fin de ce même siècle[a 2].
Théorie du chaos. Un article de Wikipédia, l'encyclopédie libre.
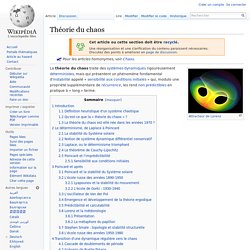
Pour les articles homonymes, voir Chaos. La théorie du chaos traite des systèmes dynamiques rigoureusement déterministes, mais qui présentent un phénomène fondamental d'instabilité appelé « sensibilité aux conditions initiales » qui, modulo une propriété supplémentaire de récurrence, les rend non prédictibles en pratique à « long » terme. Calcul stochastique. Un article de Wikipédia, l'encyclopédie libre.
Le calcul stochastique est l’étude des phénomènes aléatoires dépendant du temps. À ce titre, c'est une extension de la théorie des probabilités. Applications[modifier | modifier le code] Le domaine d’application du calcul stochastique comprend la mécanique quantique, le traitement du signal, la chimie, les mathématiques financières, la météorologie, et même la musique. Effet stochastique. Un article de Wikipédia, l'encyclopédie libre.

Par opposition aux effets dits déterministes, les effets stochastiques n'apparaissent pas selon le principe d'une cause qui induit toujours le même effet. Ils concernent par exemple les effets de faibles doses de toxiques, ou les effets des rayonnements ionisants néfastes à la santé. Calculateur stochastique. Un article de Wikipédia, l'encyclopédie libre.
Un calculateur stochastique est un concept déjà ancien (pour la jeune histoire de l'informatique) et contemporain de recherches et applications développées à la toute fin de la décennie 1950 et jusqu'au milieu de la décennie 1970. Leur définition dans le Grand Larousse encyclopédique est : « Calculateur dans lequel l'information est codée par une probabilité » Le problème[modifier | modifier le code] Calcul numérique[modifier | modifier le code] Jusque vers le milieu des années 1970, les ordinateurs étaient coûteux et il n'était pas question d'en associer un à chaque processus industriel qu'on devait surveiller ou commander. Matrice stochastique. Un article de Wikipédia, l'encyclopédie libre.
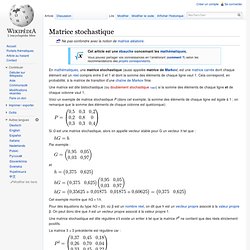
Une matrice est dite bistochastique (ou doublement stochastique (en)) si la somme des éléments de chaque ligne et de chaque colonne vaut 1. Voici un exemple de matrice stochastique P (dans cet exemple, la somme des éléments de chaque ligne est égale à 1 ; on remarque que la somme des éléments de chaque colonne est quelconque): Si G est une matrice stochastique, alors on appelle vecteur stable pour G un vecteur h tel que : Par exemple : et Cet exemple montre que hG = 1h.
Équation différentielle stochastique. Processus stochastique. Un article de Wikipédia, l'encyclopédie libre.
Le calcul classique des probabilités concerne des épreuves où chaque résultat possible (ou réalisation) est mesuré par un nombre, ce qui conduit à la notion de variable aléatoire. Un processus stochastique ou processus aléatoire (voir Calcul stochastique) ou fonction aléatoire (voir Probabilité) représente une évolution, discrète ou à temps continu, d'une variable aléatoire. Cette notion se généralise à plusieurs dimensions. Un cas particulier important, le champ aléatoire de Markov, est utilisé en analyse spatiale. Déterminisme.
Un article de Wikipédia, l'encyclopédie libre. Le déterminisme est une notion philosophique selon laquelle chaque événement est déterminé par un principe de causalité. Définition[modifier | modifier le code] Le déterminisme est la théorie selon laquelle la succession des événements et des phénomènes est due au principe de causalité, ce lien pouvant parfois être décrit par une loi physico-mathématique qui fonde alors le caractère prédictif de ces derniers. Le déterminisme ne doit être confondu ni avec le fatalisme ni avec le nécessitarisme. Le nécessitarisme affirme la nécessité des phénomènes en vertu du principe de causalité, qui fait que, dans les mêmes conditions, les mêmes causes produisant les mêmes effets, rien n'arrive qui ne soit nécessaire et qui ne pouvait être prédit de toute éternité. On distingue schématiquement le déterminisme régional et le déterminisme universel.