

Le number PI: doc word. Idée de plan. Autre. PI. Pi is a name given to the ratio of the circumference of a circle to the diameter.
That means, for any circle, you can divide the circumference (the distance around the circle) by the diameter and always get exactly the same number. It doesn't matter how big or small the circle is, Pi remains the same. Pi is often written using the symbol and is pronounced "pie", just like the dessert. Le nombre Pi. Qu'est-ce que le nombre p ?

"p = 3,14" comme on dit ... Idées d'activités. Pi Day: Pi Activities & Links. Materials large sheet of drawing paper or cardboard meterstick pen toothpicks (30 or more) calculator To Do and Notice Draw a series of parallel lines on the paper or cardboard, as many as will fit, making sure that the distance between each line is exactly equal to the length of your toothpicks.

Now, one by one, randomly toss toothpicks onto the lined paper. Keep tossing until you’re out of toothpicks—or tired of tossing. It’s time to count. First, remove any toothpicks that missed the paper or poke out beyond the paper’s edge. The Pi-Search Page. Origine/historique. Pi Day: History of Pi. Pi has been known for almost 4000 years—but even if we calculated the number of seconds in those 4000 years and calculated pi to that number of places, we would still only be approximating its actual value.

Here’s a brief history of finding pi: The ancient Babylonians calculated the area of a circle by taking 3 times the square of its radius, which gave a value of pi = 3. One Babylonian tablet (ca. 1900–1680 BC) indicates a value of 3.125 for pi, which is a closer approximation. The Rhind Papyrus (ca.1650 BC) gives us insight into the mathematics of ancient Egypt. The Egyptians calculated the area of a circle by a formula that gave the approximate value of 3.1605 for pi. History. What is pi, and how did it originate? Steven Bogart, a mathematics instructor at Georgia Perimeter College, provides the following explanation: Succinctly, pi--which is written as the Greek letter for p, or --is the ratio of the circumference of any circle to the diameter of that circle.

Regardless of the circle's size, this ratio will always equal pi. In decimal form, the value of pi is approximately 3.14. But pi is an irrational number, meaning that its decimal form neither ends (like 1/4 = 0.25) nor becomes repetitive (like 1/6 = 0.166666...). Was first used for this purpose by William Jones in 1706, probably as an abbreviation of periphery, and became standard mathematical notation roughly 30 years later. Try a brief experiment: Using a compass, draw a circle. Otherwise said, if you cut several pieces of string equal in length to the diameter, you will need a little more than three of them to cover the circumference of the circle.
Calcul de Pi. Calcul de Pi selon Archimède. Archimède a inventé, vers 250 avant J-C, une méthode originale pour le calcul de l'aire d'un disque. Archimedes_pi. MC2004-Pi-Archimede. Les décimales de pi. Vous avez sans doute entendu parler du nombre qui intervient dans les formules que l’on apprenait à l’école élémentaire : pour le périmètre du cercle de rayon et pour l’aire délimitée par ce cercle (actuellement cela s’apprend en CM2 pour le périmètre et en 6ième pour l’aire).
Je me souviens aussi des valeurs approchées ( ou ou ) de ce nombre que j’ai apprises au CM1 au cours d’une leçon qui m’a marqué pour la vie. Notre instituteur nous apprit ainsi que le nombre permet de calculer le périmètre de tous les cercles, quel que soit leur rayon, et aussi l’aire des disques qu’ils délimitent. Le plus impressionnant pour moi fut d’apprendre que ce nombre a une infinité de décimales et que personne ne peut en donner la liste ni la décrire.
Le nombre a une infinité de décimales et ce sont toutes des 3 ; la suite des décimales du nombre est facile à décrire : à partir de la cinquième décimale on juxtapose des blocs identiques . Naissance des mathématiques européennes : la Grèce Vers 600 av. Qu'est-ce que c'est ? A quoi ça sert ? How Pi Works" Pi is an extremely interesting number that is important to all sorts of mathematical calculations.
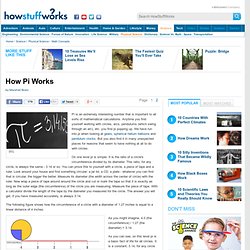
Anytime you find yourself working with circles, arcs, pendulums (which swing through an arc), etc. you find pi popping up. We have run into pi when looking at gears, spherical helium balloons and pendulum clocks. But you also find it in many unexpected places for reasons that seem to have nothing at all to do with circles. On one level pi is simple: It is the ratio of a circle's circumference divided by its diameter. This ratio, for any circle, is always the same - 3.14 or so. The following figure shows how the circumference of a circle with a diameter of 1.27 inches is equal to a linear distance of 4 inches: As you might imagine, 4.0 (the circumference) / 1.27 (the diameter) = 3.14.
As you can see, on this level pi is a basic fact of life for all circles. Check out the next page for more information about calculating pi and different things that you can do with it. MathSteps: Grade 6: Pi: What Is It? There are many fascinating numbers in mathematics.

One of the most interesting number relationships that students can discover in geometry is that the ratio of the circumference of a circle (the distance around a circle) to the diameter of a circle (the length of a line across a circle that passes through its center) is approximately equal to 3.14 or . What is Pi ? Pi. Draw a circle with a diameter (all the way across the circle) of 1 Then the circumference (all the way around the circle) is 3.14159265... a number known as Pi.
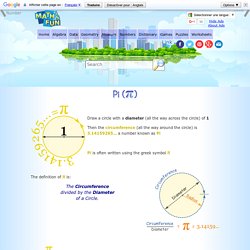
Pi.