

Blog by Dev Gualtieri. Squaring the Circle September 23, 2019 I was fascinated by the Pythagorean theorem as an elementary schoolstudent, principally because it was a bit of fundamental mathematics that was accessible to someone at my educational level.
This theorem is traditionally ascribed to the Greek philosopher, Pythagoras, who, like most of the Pre-Socratic philosophers, followed in the tradition of Thales. Thales rejected the idea that things happened at the whim of the gods and sought scientific explanations of natural phenomena. Zeno's Paradoxes. 1. Background Before we look at the paradoxes themselves it will be useful to sketch some of their historical and logical significance.
42 is the new 33 - Numberphile. The Plastic Ratio - Numberphile. 63 and -7/4 are special - Numberphile. Polyhedra. Demonstrations Project. John Savard's Home Page. Archimedean Polyhedra. Steven Dutch, Natural and Applied Sciences, University of Wisconsin - Green Bay First-time Visitors: Please visit Site Map and Disclaimer.

Use "Back" to return here. The Unsolvable Math Problem. Claim: A student mistook examples of unsolved statistics problems for a homework assignment and solved them. true Example: [Collected via Brunvand, 1987] A young college student was working hard in an upper-level math course, for fear that he would be unable to pass.
On the night before the final, he studied so long that he overslept the morning of the test.When he ran into the classroom several minutes late, he found three equations written on the blackboard. The first two went rather easily, but the third one seemed impossible. One day In 1939, Dantzig, a doctoral candidate at the University of California, Berkeley, arrived late for a graduate-level statistics class and found two problems written on the board.
Numerical Python: Numerical and Scientific Python. Introduction Comment on our own account: Since October 2015 we are working on this tutorial on numerical programming in Python.

Since then it has been the focus of our work. On the 10th of February, we started translating the documentation into German. Many scientists and engineers in the scientific and engineering world use R and MATLAB to solve their data analysis problems. It's a question troubling lots of people, which language they should choose: The functionality of R was developed with statisticians in mind, whereas Python is a general-purpose language.
Patterns - Implementing Graphs. Change notes: 2/22/98, 3/2/98, 12/4/00: This version of this essay fixes several bugs in the code.
Copyright (c) 1998, 2000, 2003 Python Software Foundation. All rights reserved. Licensed under the PSF license. Graphs are networks consisting of nodes connected by edges or arcs. Quadratic function, Linear function and Parents on Pinterest. Inverse exponential graph. 351 × 279 - math.tutorvista.com.
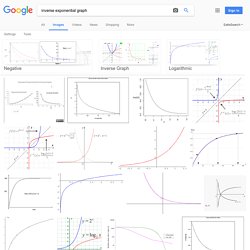
Inverse exponential graph. 4.1 - Exponential Functions and Their Graphs. Exponential Functions So far, we have been dealing with algebraic functions.
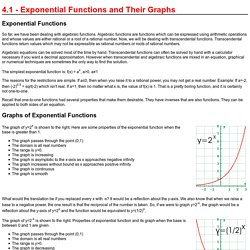
Algebraic functions are functions which can be expressed using arithmetic operations and whose values are either rational or a root of a rational number. Now, we will be dealing with transcendental functions. Transcendental functions return values which may not be expressible as rational numbers or roots of rational numbers. Algebraic equations can be solved most of the time by hand. The simplest exponential function is: f(x) = ax, a>0, a≠1 The reasons for the restrictions are simple. Part54. Riemann for Anti-Dummies Part 54 To understand Riemann's treatment of Abelian functions, situate that discovery within the context of the history in which it arose, reaching back to the pre-Euclidean Pythagoreans of ancient Greece, and forward to LaRouche's unique and revolutionary discoveries in the science of physical economy.

The Pi-Search Page. Top 10 Fascinating Mathmatics Anomalies. Suggested by SMS The process of discovery starts when we realize something is unusual or unexpected in nature – not fitting in our view of how things should happen in everyday life.

By exploring these anomalies that challenge our basic assumptions on math and science, we can discover a deeper personal understanding of the issue and learn to see nature in a different way. Interesting Anomalies in the Digits of Pi - Graham Hancock Official Website. About G.

Gene Ladner Born and raised in Houston, Texas, I’ve had a wide variety of interests in hobbies throughout my life of 59 years, such as woodcarving, windsurfing, and even rattlesnake hunting, but my recent years of “coincidence collecting” have been nothing short of life-altering. My foray into intentional collection of coincidences began rather innocently when I used the digits of Pi to generate a page number in my only dictionary at the time, just to see what might develop.
The results seemed quite fantastic to me, so I did it again, and found similar results. National Curve Bank: A Math Archive. Vector Calculus Bridge Project JAVA #64 Renie Award 2007 - A Trio of Contributors: Hamilton, Maxwell, Gibbs Wavelets #65 Introduction Wavelets Part II #65 Matrix Equations Wavelets Applications Compression AP Calculus Graphing Calculator AB Level #52 A Review BC Level #56 A Review Brachistochrone #58 Renie Award 2006 Brachistochrone II Derivation and History Brachistochrone III Bernoulli's Figures Brachistochrone IV #60 Euler-Lagrange Brachistochrone V Model from Florence Pursuit Family of Curves Deposit #59 Pursuit Java Applet Deposit #66 Interactive Trig Applet Deposit #55 Calculus: Area ~Solid of Rev. #37 Renie 2005. Desmos Graphing Calculator.