

Cédric Villani explique le Nombre d'or au Futuroscope. Fractales - A la recherche de la dimension cachée.avi. Donald au Pays des Mathémagiques (1959) - Walt Disney. Dimensions Accueil. Un film pour tout public.

Neuf chapitres, deux heures de maths, pour découvrir progressivement la quatrième dimension. Vertiges mathématiques garantis! Trouvez des informations supplémentaires pour chaque chapitre : voir "En détail". Cliquez sur l'image à gauche pour voir la bande-annonce (branchez vos haut-parleurs). Ce film est diffusé sous une licence Creative Commons. Maintenant avec encore plus de langues de commentaires et sous-titres : Commentaires en allemand, anglais, arabe, espagnol, français, italien, japonais et russe. Dimensions Chapitre 1. Les plans perpendiculaires à l'axe coupent la sphère sur des cercles qu'on appelle des parallèles.
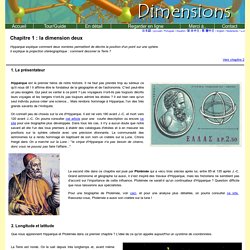
Dimensions - Chapitre 1 - Français. Dimensions Chapitre 2. Dans le film, on voit les cinq polyèdres réguliers qui traversent le plan et on montre les sections/polygones qui se déforment.

Ce n'est pas facile car les sections dépendent de la manière dont les polyèdres traversent le plan. Par exemple, si un cube se présente de manière qu'une de ses faces soit parallèle au plan, il n'y a pas de surprise : les sections sont des carrés. Mais si on coupe un cube par un plan qui passe par son centre et qui est perpendiculaire à une diagonale, l'intersection est un... hexagone régulier et ceci est peut-être moins évident ?! Après avoir regardé tous les polyèdres traverser le plan, Escher vous propose des exercices.
Dimensions - Chapitre 2 - Français. Dimensions Chapitres 3 et 4. Puis le 24, cet objet dont nous pensons que Schläfli était le plus fier !
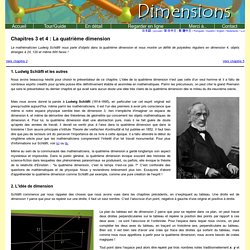
La raison est que ce nouveau venu est vraiment nouveau ; il ne généralise en aucun cas un polyèdre de dimension 3, comme dans le cas des autres polyèdres. De plus, il a cette propriété merveilleuse d'être autodual : par exemple, il a autant de faces de dimension 2 que de faces de dimension 1 (les arêtes) et autant de faces de dimension 3 que de faces de dimension 0 (les sommets). Et enfin, nous voyons les polyèdres 120 et 600 dont nous avions déjà vu les sections. Cette nouvelle vue nous montre d'autres aspects de ces polyèdres de dimension 4, qui sont décidément bien compliqués. Ces deux méthodes, les sections et les ombres, ont des avantages, mais il faut reconnaître qu'ils ne rendent pas justice à toutes les symétries de ces magnifiques objets.
Dans le chapitre suivant, nous utiliserons une autre méthode, celle de la projection stéréographique ! (Voir le film Chapitre 4 : la quatrième dimension, suite) Dimensions - Chapitre 3 - Français. Dimensions - Chapitre 4 - Français. Dimensions Chapitres 5 et 6. Deux notions seront utiles pour la suite : Le module d'un nombre complexe z= x +i y est simplement la distance du point correspondant (x,y) à l'origine.

On le note |z| et il est égal, d'après le théorème de Pythagore à √ (x2+y2) . Par exemple, le module de i est égal à 1 et celui de 1+i à √2. L'argument indique la direction de z. On le note Arg(z) et ce n'est rien d'autre que l'angle entre l'axe des abscisses et la droite joignant l'origine à (x,y). Les mathématiciens ont longtemps essayé de faire la même chose dans l'espace de dimension 3 : comment multiplier des points dans l'espace ? En résumé, les points du plan sont définis par un seul nombre... complexe. Dimensions - Chapitre 5 - Français. Dimensions - Chapitre 6 - Français. Dimensions Chapitre 7 et 8. Rappelons-nous la formule qui exprime la projection de Hopf.

En termes des coordonnées complexes, elle envoie (z1,z2) sur le point a=z2/z1 considéré comme un point de S2. Fixer un parallèle p dans S2, c'est fixer le module d'un nombre complexe, si bien que l'image réciproque d'un parallèle est décrite par une équation de la forme |z2/z1| = constante. Choisissons par exemple 1 pour cette constante si bien que z1 et z2 ont le même module. Dimensions - Chapitre 7 - Français.
Dimensions - Chapitre 8 - Français. Dimensions Chapitre 9. Dimensions - Chapitre 9 - Français. "Comment j'ai détesté les maths", pour voir les maths autrement. Ils sont nombreux à détester les maths et à le faire savoir.
Dans "Comment j'ai détesté les maths", le réalisateur français Olivier Peyon se penche sur un rejet répandu mais qui, selon lui, a de quoi interpeller dans la société actuelle. "De tout temps, on a détesté les maths. Victor Hugo écrivait des textes là-dessus... Mais ce qui a changé, c’est que les maths ont pris une telle importance, que ce soit à l’école ou dans la technologie, qu’on ne peut plus les détester tranquillement", explique le réalisateur français. "Maintenant, à défaut de les aimer, on peut au moins tenter de comprendre ce qui se cache derrière. " Car les maths sont partout. Pour Jean-Pierre Bourguignon, le président du Conseil européen de la recherche, qui a participé au tournage, les maths sont un enjeu économique crucial pour l'Europe.
"Formules diaboliques" A quoi servent les mathématiques ? « À quoi servent les mathématiques ?
» se sont demandé des générations d'élèves fixant désespérément le tableau noir ou leur feuille à petits carreaux. Et il faut bien admettre que dans notre vie quotidienne ou professionnelle, très peu d'entre nous les utilisent. Comment attirer les enfants vers cette science souvent considérée comme « trop abstraite » ?
Que sont aujourd'hui les mathématiques de haut niveau ? Quelles applications concrètes trouvent-elles dans la société ? Paiement sécurisé Il y a 65 millions d’années, la collision d’un astéroïde avec la Terre fut la cause principale de la disparition des dinosaures. Tous sur orbites !