

Are AES 256-bit keys too large? This may seem an odd question given that since the mid 70's discussions about cryptographic keys have been mainly concerned about their potential shortness.
While the risks of using short keys are apparent, there are risks lurking at the other end of the gamut as well. We can have too much of a good thing, and also think we have a good thing when we in fact don't. The adoption of the AES cipher has progressed quite rapidly, greatly assisted by being mandated as a US government standard. As a technology AES has nonchalantly skipped along the Gartner hype cycle and nestled into the Plateau of Productivity. AES supports key lengths of 128, 192 and 256 bits, and many commercial offerings, to encrypt laptops or USB sticks for example, supply AES at the maximum 256-bit key length. The economics of AES keys Modern block ciphers encrypt by mixing data over a series of rounds to produce a complex nonlinear relationship between the plaintext (message), ciphertext and key.
AES and Passwords. So you want to use an alternative cipher... Once in a while I run into discussions that hinge on the following dubious proposition: that AES is bad and we need to replace it.
These discussions always make me leery, since they begin with facts not in evidence, and rarely inspire any confidence that the solution is going to be any better than the 'problem'. In fact, this whole point of view is so rarified that I've debated whether to even write this post, since my opinion is that AES is the last place your system is going to break down -- and you should be focusing your attention on fixing all the other broken things first. Moreover, the simple advice on AES mirrors the ancient wisdom about IBM: nobody ever got fired for choosing it.
The KECCAK Effect - What SHA-3 Brings to the Table. The National Institute of Standards and Technologies (NIST) announced on the 2nd of October that the winner of the SHA-3 competition is KECCAK (pronounced ketchack).
Interestingly, it was 12 years ago to the day that NIST announced the Advanced Encryption Standard (AES) algorithm. Cryptographic sponge functions. Eve's SHA3 candidate: malicious hashing. Letter Frequencies. The frequency of letters in text messages has often been studied for use in cryptography, and frequency analysis in particular.
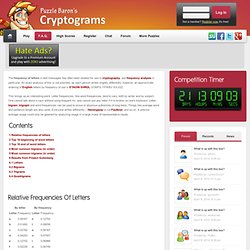
An exact analysis of this is not possible, as each person writes slightly differently; however, an approximate ordering of English letters by frequency of use is ETAOIN SHRDL UCMFG YPWBV KXJQZ. This brings up an interesting point. Letter frequencies, like word frequencies, tend to vary, both by writer and by subject. One cannot talk about x-rays without using frequent Xs, and cannot use any letter if it is broken on one's keyboard. 2013 - Interview: Gilles Van Assche:<br/>Keccak, More Than Just SHA3SUM. FOSDEM 2013/Interviews/Gilles Van Assche: Keccak, More Than Just SHA3SUM Gilles Van Assche and Joan Daemen will give a talk about Keccak, More Than Just SHA3SUM at FOSDEM 2013 Q: Could you briefly introduce yourself?
We, Guido, Joan, Michaël and Gilles (a.k.a. the Keccak Team), are cryptographers working at STMicroelectronics (Guido, Joan, Gilles) and NXP (Michaël). Creating a Cryptographic Hash Function. A Cryptographic hash function is something that mechanically takes an arbitrary amount of input, and produces an "unpredictable" output of a fixed size.
The unpredictableness isn't in the operation itself. Obviously, due to its mechanical nature, every time a given input is used the same output will result. It means that you cannot easily craft an input to produce a wanted output, or similarly guess what input produced a given output; Easily create two different inputs that give the same output hash; Easily create a suffix or prefix to a given input to create a wanted hash; Or in different terms, distinguish the output from an abstract "Random Oracle". This differs from non-cryptographic hash functions used for high-speed hash-tables or other data structures. Those are designed to produce high enough quality statistical randomness to fulfil their purposes.
An ideal hash function produces an output of n bits. A Stick Figure Guide to the Advanced Encryption Standard (AES) (A play in 4 acts.
Please feel free to exit along with the stage character that best represents you. Take intermissions as you see fit. Click on the stage if you have a hard time seeing it. If you get bored, you can jump to the code. Most importantly, enjoy the show!) Act 1: Once Upon a Time... Act 2: Crypto Basics Act 3: Details Act 4: Math! Epilogue I created a heavily-commented AES/Rijndael implementation to go along with this post and put it on GitHub. The Design of Rijndael is the book on the subject, written by the Rijndael creators. Please leave a comment if you notice something that can be better explained. Update #1: Several scenes were updated to fix some errors mentioned in the comments.Update #2: By request, I've created a slide show presentation of this play in both PowerPoint and PDF formats.