

An English professor just won $700,000 for solving a 379-year-old maths problem. Wiles' proof of Fermat's Last Theorem. The proof itself is over 150 pages long and consumed seven years of Wiles' research time.[1] John Coates described the proof as one of the highest achievements of number theory, and John Conway called it the proof of the century.[2] For solving Fermat's Last Theorem, he was knighted, and received other honours such as the 2016 Abel Prize.
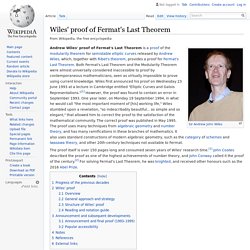
Progress of the previous decades[edit] Fermat's Last Theorem, formulated in 1637, states that no three distinct positive integers a, b, and c can satisfy the equation if n is an integer greater than two. In the 1950s and 1960s the modularity theorem, a connection between elliptic curves and modular forms, was conjectured by the Japanese mathematician Goro Shimura based on ideas posed by Yutaka Taniyama. Mathematicians have discovered a strange pattern hiding in prime numbers.
Mathematicians are pretty obsessed with prime numbers - those elusive integers that can only be divided by one and themselves.
If they're not creating cool artworks with them or finding them in nature, they're using computers to discover increasingly larger primes. Mathematicians Discovered Something Super Freaky About Prime Numbers. The maths problem that’s gone viral: When the hell is Cheryl’s birthday? A few days ago, Singaporean television host Kenneth Kong posted the below maths question on his Facebook page, and it went viral.
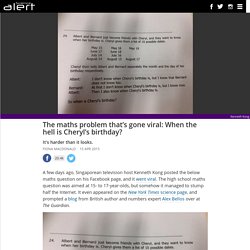
The high school maths question was aimed at 15- to 17-year-olds, but somehow it managed to stump half the Internet. It even appeared on the New York Times science page, and prompted a blog from British author and numbers expert Alex Bellos over at The Guardian. So when exactly is Cheryl's birthday, and why is the problem so frustrating for so many adults? Before we get to the solution, let's clear up any ambiguity with the wording, which Kenneth Chang over at The New York Times calls "terrible".
To start with, Cheryl (who we can only imagine has set her birthday to private on Facebook) will only give Albert and Bernard 10 possible dates for her birthday. May 15, May 16, May 19 June 17, June 18 July 14, July 16. A purported new mathematics proof is impenetrable – now what? What happens when someone claims to have proved a famous conjecture?
Well, it depends. When a paper is submitted, the journal editor will pass it off to a respected expert for examination. That referee will then scan the paper looking for a significant new idea. If there isn’t one, then the whole argument is unlikely to get much more scrutiny. Dunbar's number. Mathematical graffiti surprise. ExcelPython. Faster Integration with the Tanh-Sinh Method. In my previous post about numerical integration I mentioned that I would be writing about another lesser known method providing better speed and/or accuracy in many cases.
The method is known as Tanh-Sinh quadrature, and has been implemented in Excel by a reader of this blog, Graeme Dennes. Graeme has incorporated a Tanh-Sinh function along with functions for the Gauss-Kronrod method and the Romberg method, and compared their performance at calculating the integrals of 55 different functions.
The spreadsheet (including full open source code and extensive notes) may be downloaded from: Tanh-Sinh.zip. Graeme’s notes on the origins of the method and its advantages are given below, together with some screen shots of the output. by Graeme Dennes Introduction: This Excel VBA workbook provides three single-dimension quadrature programs as User Defined Functions (UDF) for calculating the definite integral of a non-oscillatory analytic function over a finite interval (a,b). Key Purposes: 1. Newton Excel Bach, not (just) an Excel Blog. Hero of Alexandria.
Hero of Alexandria (Greek: Ἥρων ὁ Ἀλεξανδρεύς, Heron ho Alexandreus; also known as Heron of Alexandria c. 10 – c. 70 AD) was a Greek mathematician and engineer who was active in his native city of Alexandria, Roman Egypt.
He is considered the greatest experimenter of antiquity[1] and his work is representative of the Hellenistic scientific tradition.[2] Hero published a well recognized description of a steam-powered device called an aeolipile (sometimes called a "Hero engine"). Among his most famous inventions was a windwheel, constituting the earliest instance of wind harnessing on land.[3][4] He is said to have been a follower of the Atomists. Some of his ideas were derived from the works of Ctesibius. Much of Hero's original writings and designs have been lost, but some of his works were preserved in Arabic manuscripts.
Career[edit] Inventions[edit] Mathematics[edit] In media[edit] Bibliography[edit] Works known to have been written by Hero: History, Travel, Arts, Science, People, Places. Searching for the World's First Zero Mathematicians consider the invention (or discovery, depending on your point of view) of zero as one of the most important intellectual advances humans have ever made.
Why? Isn't zero just sheer nothingness? Nothing could be further from the truth. Zero is not only a concept of nothingness, which allows us to do arithmetic well and to algebraically define negative numbers, but it is also an important place-holding device. Coulomb's constant.
Geometry. Mathematicians have discovered a strange pattern hiding in prime numbers.