

Base converter. Lattice Multiplication. Jain's True Value of Pi. I will be releasing a new body of work that gives the True Value of Pi, based on the Harmonics of Phi (1.618033...), a value close to 3.144...

The ancient Mathematics masters have always known that the two most important transcendental numbers Pi and Phi are intimately related. Name a Theorem. By placing an order with TheoryMine, you name a newly discovered mathematical theorem¹.

This lets you immortalise your loved ones, teachers, friends and even yourself and your favourite pets! Mathematical immortality? Name that theorem - physics-math - 03 December 2010. By Jacob Aron During my time as an eager undergraduate mathematician, I’d often wonder what it would feel like to prove a truly new result and have my name immortalised in the mathematical history books.

I thought that dream had died when I gave up maths to become a science writer, but Aron’s theorem is now a reality – and I’ve got the certificate to prove it. While most mathematical theorems result from weeks of hard work and possibly a few broken pencils, mine comes courtesy of TheoryMine, a company selling personalised theorems as novelty gifts for £15 a pop. 2011 preview: Million-dollar mathematics problem - physics-math - 27 December 2010.
By Michael Reilly Read more: “In with the New Scientist: Our predictions for 2011” Gentlemen – and women – plug in your engines.

This will be the year of the electric car. No, seriously. After seemingly endless testing, technical hiccups and plain reluctance on the part of manufacturers to move electric vehicles from the concept phase to the showroom, it’s finally happening. Leading the charge is the Chevy Volt. Even if the Volt fizzles, the Nissan Leaf, Ford Focus Electric and Renault Fluence will all be widely available in the next 12 months. Two factors have combined to bring electric cars to the mass market at last: the arrival of high-capacity batteries and the near-collapse of the American auto industry, which forced US car makers into building small, efficient vehicles that can compete with foreign offerings. The biggest remaining obstacle is cost. Make way for mathematical matter - physics-math - 05 January 2011. Editorial: "The deep value of mathematics" WE ALREADY have solid, liquid, gas, plasma and Bose-Einstein condensate.
Π really is wrong! I've written recently about several different crackpots who insist, for a variety of completely ridiculous reasons, that is wrong.
Happy Tau Day? « Math Goes Pop! In the past, I’ve used this blog as a platform to make clear my mixed feelings about Pi Day, a math themed holiday celebrated every year on March 14th (3/14, har har) in honor of the beloved mathematical constant .
My thoughts on the subject can be found here. It would seem that I am not alone in my frustration. Michael Hartl, an educator and entrepreneur (as well as a Ph.D. graduate from Caltech), has just today launched a website in favor of Tau Day as a replacement for Pi Day. Why we have to get rid of pi for the sake of good math. Ancient puzzle gets new lease of 'geomagical' life - physics-math - 24 January 2011. An ancient mathematical puzzle that has fascinated mathematicians for centuries has found a new lease of life.
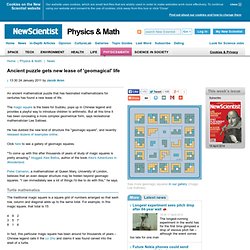
The magic square is the basis for Sudoku, pops up in Chinese legend and provides a playful way to introduce children to arithmetic. But all this time it has been concealing a more complex geometrical form, says recreational mathematician Lee Sallows. He has dubbed the new kind of structure the "geomagic square", and recently released dozens of examples online. Click here to see a gallery of geomagic squares. Deep meaning in Ramanujan's 'simple' pattern - physics-math - 27 January 2011. By Jacob Aron The first simple formula has been found for calculating how many ways a number can be created by adding together other numbers, solving a puzzle that captivated the legendary mathematician Srinivasa Ramanujan.

The feat has also led to a greater understanding of a cryptic phrase Ramanujan used to describe sequences of so-called partition numbers. A partition of a number is any combination of integers that adds up to that number. For example, 4 = 3+1 = 2+2 = 2+1+1 = 1+1+1+1, so the partition number of 4 is 5. It sounds simple, yet the partition number of 10 is 42, while 100 has more than 190 million partitions. Previous attempts have only provided approximations or relied on “crazy infinite sums”, says Ken Ono at Emory University in Atlanta, Georgia. Someone told me that if there are 20 people in a room, there's a 50/50 chance that two of them will have the same birthday. How can that be?" This phenomenon actually has a name -- it is called the birthday paradox, and it turns out it is useful in several different areas (for example, cryptography and hashing algorithms).
You can try it yourself -- the next time you are at a gathering of 20 or 30 people, ask everyone for their birth date. It is likely that two people in the group will have the same birthday. It always surprises people! The reason this is so surprising is because we are used to comparing our particular birthdays with others. For example, if you meet someone randomly and ask him what his birthday is, the chance of the two of you having the same birthday is only 1/365 (0.27%).
When you put 20 people in a room, however, the thing that changes is the fact that each of the 20 people is now asking each of the other 19 people about their birthdays. If you want to calculate the exact probability, one way to look at it is like this. Why-couldnt-i-have-been-shown-this-in-maths-class.gif (GIF Image, 251x231 pixels) Stephen Wolfram: Computing a theory of everything.
Nerd Paradise : Divisibility Rules for Arbitrary Divisors. It's rather obvious when a number is divisible by 2 or 5, and some of you probably know how to tell if a number is divisible by 3, but it is possible to figure out the division 'rule' for any number. Here are the rules for 2 through 11... The last digit is divisible by 2. The sum of all the digits in the number is divisible by 3. The last 2 digits are divisible by 4. The last digit is 5 or 0. Arthur Benjamin does "Mathemagic" Folding Paper in Half Twelve Times. Folding Paper in Half 12 Times: The story of an impossible challenge solved at the Historical Society office Alice laughed: "There's no use trying," she said; "one can't believe impossible things.
" "I daresay you haven't had much practice," said the Queen. Through the Looking Glass by L. Carroll The long standing challenge was that a single piece of paper, no matter the size, cannot be folded in half more than 7 or 8 times. The most significant part of Britney's work is actually not the geometric progression of a folding sequence but rather the detailed analysis to find why geometric sequences have practical limits that prevent them from expanding. Her book provides the size of paper needed to fold paper and gold 16 times using different folding techniques.
Britney Gallivan has solved the Paper Folding Problem. In April of 2005 Britney's accomplishment was mentioned on the prime time CBS television show Numb3rs. The task was commonly known to be impossible. Hypotrochoid_R_equals_7,_r_equals_2,_d=3.gif (GIF Image, 400x400 pixels) Bill the Lizard: Six Visual Proofs. 1 + 2 + 3 + ... + n = n * (n+1) / 2 1 + 3 + 5 + ... + (2n − 1) = n2 Related posts:Math visualization: (x + 1)2 Further reading:Proof without Words: Exercises in Visual ThinkingQ.E.D.: Beauty in Mathematical Proof. Mathematica Online Integrator. Calculus Mega Cheat Sheet.
What does 0^0 (zero raised to the zeroth power) equal? Why do mathematicians and high school teachers disagree. Clever student: I know! Now we just plug in x=0, and we see that zero to the zero is one! Cleverer student: No, you’re wrong! You’re not allowed to divide by zero, which you did in the last step. Weierstrass functions. Weierstrass functions are famous for being continuous everywhere, but differentiable "nowhere". Here is an example of one: It is not hard to show that this series converges for all x.
In fact, it is absolutely convergent. Web Design and Development. The On-Line Encyclopedia of Integer Sequences™ (OEIS™) Approximating Pi (non-Flash) Solve Your Calculus Problems Online. PatrickJMT. 6174 (number) 6174 is known as Kaprekar's constant[1][2][3] after the Indian mathematician D. R. Kaprekar. This number is notable for the following property: Take any four-digit number, using at least two different digits. (Leading zeros are allowed.)Arrange the digits in ascending and then in descending order to get two four-digit numbers, adding leading zeros if necessary.Subtract the smaller number from the bigger number.Go back to step 2.
Mathematicians Solve 140-Year-Old Boltzmann Equation. Unsolved Problems. Wolfram MathWorld: The Web's Most Extensive Mathematics Resource.