

GEOMETRIE FACILE: L´étoile à 8 branches, modèle nº 2. Partager en 4. Partager en 8. Étoile à 8 branches. Avec un compas et une règle.
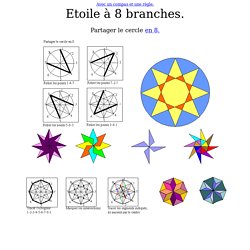
Partager en 8. Une m thode simple et complete, accessible tous et gratuite, d'apr s mon livre Parcelles d'infini. Mise en ligne gratuite de mon livre "Parcelles d'infini - Promenade au jardin d'Escher"publié aux Éditions Pour la Science, ISBN 2-84245-075-2, en 2005 Avec tous mes remerciements à David Bailey www.tess-elation.co.uk pour son aide précieuse concernant la traduction.

Sommaire Avant-propos L’inventeur a, tout à coup, le sentiment très netque les conceptions auxquelles il vient de parvenir (…)existaient déjà avant d’avoir jamais été pensées dans le cerveau humain. Louis de BROGLIE Ma chanson n’est vraiment terminée que lorsqu’elle a l’air de s’être faite toute seule. C’est une sensation que je ressenschaque fois que j’exécute un projet de remplissage périodique d’un plan.Il me semble que ce n’est pas «moi» qui décide des formes mais que ces simples taches sur lesquelles je me penche ont leur propre volonté,que ce sont elles qui guident le mouvement de ma main.
Exoststd2a pavages. Le coussin en carrelage. On ne joue pas avec la nourriture – Bluette. J’époussette un peu le blog aujourd’hui pour vous parler d’un drôle de biscuit.
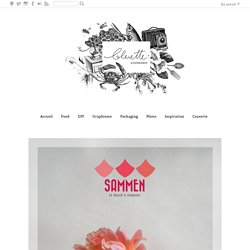
Plus précisément d’une fausse marque de biscuit. Fin avril j’ai participé à un atelier impression 3D au BHV avec le Fabshop dont le thème était l’expérimentation culinaire. J’ai notamment eu la possibilité d’imprimer un emporte-pièce dessiné par mes soins. Je vous parlerais de l’impression 3D dans un prochain billet, mais pour ceux qui ne connaîtraient pas, il est possible d’imprimer « physiquement » (en plastique, métal, céramique, chocolat…) des objets dessinés grâce aux logiciels de modélisation 3D. Des objets uniques, complètement personnalisés puisque c’est vous qui les créez. Revenons à nos biscuits.
Après quelques croquis voici donc la forme que j’ai retenue : Une fois l’emporte-pièce imprimé (je vous expliquerais tout ça en détail prochainement), il fallait le tester. Si vous souhaitez apprendre à faire le glaçage royal, vous pouvez suivre les explications très claires de Jessica. Trackofthepast. English version : « D’un geste machinal, il jette un coup d’œil au module de contrôle.
La charge est bonne et les voyants sont au vert, parfait pour passer une bonne nuit en sachant que demain matin, il y aura du courant pour faire chauffer la cafetière, griller les toasts et surtout pour la grande fiesta du soir. Il est vrai que ce vent d’ouest bien établi et la quantité d’eau qui est tombé hier soir ont permis de regonfler la réserve d’énergie. » Nous ne sommes pas dans un roman de science fiction mais face à ce qui pourrait devenir dans un avenir proche le quotidien de monsieur tout le monde. Notre personnage aurait pu se laisser séduire par une solution clé en main amortissable sur des décennies sans garantie de rentrer un jour dans ses frais ; le tout assorti d’un contrat de maintenance exclusif. L’énergie ouverte qu’est ce que c’est ? L’idée est simple. Elle apparaît comme une alternative Low Tech où l’utilisateur redevient acteur.
L’utilisateur est au cœur du système. Pavage d'Alger - GeoGebra. Pour créer un motif de pavage - GeoGebra. Les oiseaux paveurs. Le pavage : jeu Tu vas paver le cadre ci-dessous avec des oiseaux.

Il doit donc être rempli sans trou ni chevauchement. Le bouton N te donne un nouveau gabarit d'oiseau que tu devras positionner autour de celui ou de ceux qui sont déjà placés. Les boutons fléchés permettent de faire tourner le gabarit. Quand le gabarit est correctement placé, il est alors fixé à sa place. ATTENTION ! Methode de l'enveloppe pour construire un motif de pavage. Image Categories – Symmetry. Transformations, pavage et art - Autonom'Maths. J'aime beaucoup les œuvres d'Escher, j'utilisais les figures impossibles pour expliquer qu'il fallait démontrer et ne pas se contenter d'une figure.
Pour poursuivre mes travaux de groupes, j'ai eu envie que chaque groupe réalise un pavage à partir des figures de bases d'Escher. Évidemment, je ne voulais pas donner la même figure de départ à tout le monde pour plusieurs raisons : pour avoir plus d'affiches dans ma salle et surtout pour faire apparaître différentes transformations du plan. Certains n'ont que des translations (avec Beetle), d'autres des symétries ou des rotations... Bref, il y a plein de possibilités à exploiter ! Voici mon fichier de base pour les élèves : Mathématiques - mur et pavages. Espace pédagogique > disciplines du second degré > mathématiques > enseignement > actions nationales > actions nationales 2015-2017 mis à jour le 19/04/2016.
Pavage : de GeoGebra à Scratch. Mathematiques. Mathématiques - actions nationales 2015-2016. Mathématiques - mur et pavages. Mathématiques - premiers pas. Mathématiques - démarrer avec scratch. Jeux Blocky : Labyrinthe. Jeux BlockyPuzzleLabyrintheOiseauTortueMovieTutoriel de PondPondVous avez résolu ce niveau avec 1 ligne de JavaScript :Vous avez résolu ce niveau avec %1 lignes de JavaScript :Êtes-vous prêt pour le niveau %1 ?
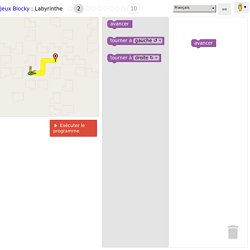
Êtes-vous prêt pour le prochain défi ? Sauvegarder et lier aux blocs. Lancer le programme que vous avez écrit.Exécuter le programmeArrêter le programme et réinitialiser le niveau.RéinitialiserAideOKAnnulerLogiqueBouclesMathématiquesTexteListesCouleurVariablesFonctionsIl y a eu un problème avec la demande.Partagez vos blocs grâce à ce lien: %1Désolé, '%1' ne correspond à aucun programme sauvegardé.Impossible de charger le fichier de sauvegarde. Peut être a t-il été créé avec une autre version de Blockly? Listetexte Ce niveau est très difficile. Mathématiques - commande au restaurant.
Les élèves disposent d'un bon de commande et de la carte des menus du restaurant : Après un temps de réflexion individuelle, les élèves ont établi par groupe une facture pour la table n°3.

Voici un exemple de ce qu'ils ont produit (toutes les propositions étant relativement ressemblantes). Les élèves doivent ensuite concevoir ( toujours sur papier) une application que l'on pourrait installer sur une tablette et qui permettrait de prendre la commande et d'annoncer aussitôt le montant de la facture. Les propositions sont alors projetées en classe et chaque groupe explique le fonctionnement. 2 démarches apparaissent dans les propositions : Mathématiques - commande au restaurant. Mathématiques - mini gps. Espace pédagogique > disciplines du second degré > mathématiques > enseignement > actions nationales > actions nationales 2015-2016 mis à jour le 26/12/2015 Comment aborder l'algorithmique en partant d'une situation concrète : rejoindre le musée en partant du collège. mots clés : algorithmique, TraAM, déplacement Déroulement de la séance La séance se déroule en plusieurs temps (sur 3h) avec notamment des allers-retours entre la programmation et la recherche papier.Les élèves sont par îlot et travaillent par groupe de 3 ou 4. 1er temps : le tracé et une première description.
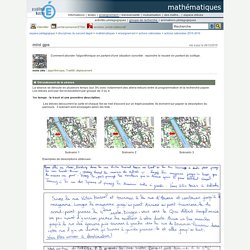
Les élèves découvrent la carte et chaque îlot se met d'accord sur un trajet possible. Exemples de descriptions obtenues : Mathématiques - scratch des idées à prendre ou à laisser... Learn. Play, Design & Code Retro Arcade Games Grades 2+ | Blocks CS First Unplugged. Mathématiques - tableau de fil. Cette activité a été proposée à des élèves de 4ème qui avaient déjà fait l’activité « mur et pavage ». Elle a été présentée de la même manière. Les élèves sont partis rapidement sur des blocs (« croix », « en haut à gauche », « en haut à droite », « en bas à gauche » et « en bas à droite »).
Le dessin se faisant trop vite, ils m’ont demandé comment le ralentir, ce qui m’a permis d’introduire la commande « glisser ». D’autres élèves ont voulu savoir si le dessin pouvait se faire « tout en même temps » plutôt que par « quart ». Ils ont donc décidé de tracer des quadrilatères plutôt qu’une succession de lignes. Mathématiques - marche aléatoire. Nous sommes en salle multimédia. Deux élèves par poste (je ne peux pas faire autrement… : 15 postes pour 28 élèves). L’interface Scratch qu’ils ont déjà découverte une fois et le fonctionnement des blocs (par glisser-déposer) ne posent pas de souci. Je propose aux élèves de programmer une marche aléatoire du lutin du bas de l’écran vers le haut de l’écran avec comme consigne qu’à chaque déplacement, que l’ont va répéter un grand nombre de fois, le lutin avance « aléatoirement » soit « en diagonale vers la gauche » (orientation à - 45°) soit en « diagonale vers la droite » (orientation à 45°).
Je précise aux élèves que l’opérateur pourra être utile et que je les invite à faire fonctionner plusieurs fois leur programme pour en observer les résultats. On apprécie ici la simplicité du programme mais on constate qu’il ne correspond pas tout à fait à la consigne : il y a 3 déplacements possibles. Mathématiques - mur et pavages. Mathématiques - mini gps. Mathématiques - mini gps. Classic Maze. Mathématiques - quelques constructions géométriques. Pour les plus rapides d’abord, puis au fur à mesure pour tous les binômes, je propose une dernière construction : « une figure à 5 côtés… c’est à dire ?....
» « Un pentagone ? »« Bien Laura ! ».« Je vous propose de réaliser un pentagone dont les 5 côtés mesurent 90 pixels… »Remarque : je ne dessine rien… je ne précise pas « pentagone régulier » mais tous les élèves le prennent comme tel… Les recherches commencent… Les élèves n’ont pas traité d’activité sur les angles inscrits, les polygones réguliers… Je m’attendais donc à quelques difficultés… Après quelques tentatives, ils sentent que c’est la mesure de l’angle qui est la clef…Un groupe m’appelle pour me dire qu’ « ils ont trouvé !!!
Mathématiques - quelques constructions géométriques. Mathématiques - actions nationales 2015-2016. Mathématiques - quadrilatères. Espace pédagogique > disciplines du second degré > mathématiques > enseignement > actions nationales > actions nationales 2015-2016 mis à jour le 07/03/2016 Comprendre les angles avec scratch. mots clés : quadrilatère, algorithmique, TraAM Objectif Les élèves doivent terminer la programmation d'un jeu. Déroulement de la séance Le travail est prévu dans un premier pour se dérouler sur 3 séances mais 2 séances suffiront finalement.Il s'agit de la deuxième séance de travail sur Scratch avec les élèves.L'objectif du travail est annoncé aux élèves et les consignes sont distribuées.Une mise au point en classe entière est nécessaire pendant quelques minutes pour expliquer le principe du jeu.Le professeur jouant le rôle de l'ordinateur et un élève celui de l'utilisateur.Les consignes sont distribués aux élèves qui en prennent connaissances pendant quelques minutes.