

Alan Turing honoured on new £50 banknote. 15 July 2019 The Bank of England has announced its selection of Alan Turing as the character to feature on the reverse side of the new £50 banknote.
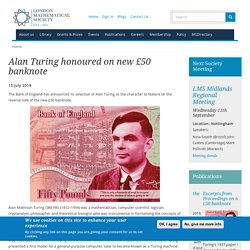
Alan Mathison Turing OBE FRS (1912–1954) was a mathematician, computer scientist, logician, cryptanalyst, philosopher and theoretical biologist who was instrumental in formalising the concepts of algorithm and computation. Turing worked as a code-breaker during the second world war and is widely accredited with having helped bring an earlier end to the war. In his article ‘On computable numbers, with an application to the Entscheidungsproblem’ (submitted 28 May 1936, published in Proceedings of the London Mathematical Society (2) 42 (1937) 230–265), Turing presented a first model for a general-purpose computer, later to become known as a ‘Turing machine’. The first excerpt is a table from page 240 which provides a schema for succinctly representing Turing machines.
Prix Schock. Problème de la décision. En logique mathématique, on appelle problème de la décision ou, sous son nom d'origine en allemand, Entscheidungsproblem, le fait de déterminer de façon mécanique (par un algorithme) si un énoncé est un théorème de la logique égalitaire du premier ordre, c’est-à-dire s'il se dérive dans un système de déduction sans autres axiomes que ceux de l'égalité (exemples : système à la Hilbert, calcul des séquents, déduction naturelle).
De façon équivalente par le théorème de complétude, il s'agit finalement de savoir si un énoncé est universellement valide, c’est-à-dire vrai dans tous les modèles (de l'égalité). Le problème de la décision est un exemple de problème de décision : une question de décidabilité au sens algorithmique. Programme de Hilbert. Le Programme de Hilbert est un programme créé par David Hilbert dans le but d'assurer les fondements des mathématiques.
Description[modifier | modifier le code] Les conceptions scientifiques de David Hilbert ont une grande influence sur les mathématiciens de l'époque. Hilbert s'oppose fermement au pessimisme scientifique prôné en particulier par le physiologiste Emil du Bois-Reymond[1], pour qui il est des questions en sciences qui resteront toujours sans réponse, une doctrine connue sous le nom d'« Ignorabimus » (du latin ignoramus et ignorabimus : « Nous ne savons pas et nous ne saurons jamais »).
Pour Hilbert, « il n'y a pas d'Ignorabimus en mathématiques » ((de) Wir müssen wissen. Énigmes logiques et paradoxes, les plus classiques. Carl G.

Hempel (1905-1997), philosophe américain, d’origine allemande, proposa ce paradoxe en 1946. Il s’agit "simplement " de vérifier que: Tous les corbeaux sont noirs. On peut rechercher les corbeaux et noter leur couleur. Chaque corbeau noir confirme l’hypothèse. Paradoxe de Hempel. Un article de Wikipédia, l'encyclopédie libre.
Post hoc ergo propter hoc. Un article de Wikipédia, l'encyclopédie libre.
Post hoc, ergo propter hoc (latin pour à la suite de cela, donc à cause de cela[1]) est un sophisme qui consiste à prendre pour la cause ce qui n'est qu'un antécédent[2], c'est prétendre que si un évènement suit un autre alors le premier doit être la cause du second. Le groupe LIGC (héritier du groupe LMP né en 2000) regroupe des philosophes et des scientifiques (...) - Logique et Interaction : vers une Géométrie de la Cognition. Style de Fitch pour la déduction naturelle. Gödel’s Incompleteness Theorem: Ontological Mathematics vs. Science. Most people think that Gödel’s Incompleteness Theorem means something about the final answer to everything being something that can never be attained, only more and more closely approximated, because any system of logic and its axioms will always be incomplete and contain inconsistent statements inevaluable as either absolutely true or false.

Similarly, Stephen Hawking wrote in the ‘Brief History of Time’ that it seemed as though science would only ever asymptote towards a final theory of everything, but never completely get there. Le théorème d'incomplétude de Godel - PS n°92. Le théorème d’incomplétude de Gödel. Paradoxe de Goodman. Un article de Wikipédia, l'encyclopédie libre.
Énoncé[modifier | modifier le code] Goodman inventa l'adjectif « vleu » (« grue » en anglais) signifiant « vert jusqu'à une certaine date t et bleu ensuite. » Raisonnement par l'absurde. Sur les autres projets Wikimedia : apagogie, sur le Wiktionnaire En philosophie[modifier | modifier le code] Apagogie positive[modifier | modifier le code] On parle d'apagogie positive ou de démonstration par l'absurde simple quand la conclusion affirme la vérité d'une proposition, non en l'établissant directement par une démonstration tirée de la nature même de la chose, mais indirectement, en faisant voir que la proposition contraire est absurde.
On conclut de la fausseté de l'une à la vérité de l'autre. Intuitionnisme. Un article de Wikipédia, l'encyclopédie libre.
L'intuitionnisme est une philosophie des mathématiques que L. E. J. Brouwer a élaborée au début du XXe siècle. Pour Brouwer, les mathématiques sont une libre création de l'esprit humain. List of paradoxes. This is a list of paradoxes, grouped thematically. The grouping is approximate, as paradoxes may fit into more than one category. Because of varying definitions of the term paradox, some of the following are not considered to be paradoxes by everyone. This list collects only scenarios that have been called a paradox by at least one source and have their own article. Although considered paradoxes, some of these are based on fallacious reasoning, or incomplete/faulty analysis. Informally, the term is often used to describe a counter-intuitive result.
Curry's paradox. Kleene–Rosser paradox. In mathematics, the Kleene–Rosser paradox is a paradox that shows that certain systems of formal logic are inconsistent, in particular the version of Curry's combinatory logic introduced in 1930, and Church's original lambda calculus, introduced in 1932–1933, both originally intended as systems of formal logic. The paradox was exhibited by Stephen Kleene and J. B. Type theory. In mathematics, logic, and computer science, a type theory is any of a class of formal systems, some of which can serve as alternatives to set theory as a foundation for all mathematics. In type theory, every "term" has a "type" and operations are restricted to terms of a certain type. Proof-theoretic semantics. Gerhard Gentzen is the founder of proof-theoretic semantics, providing the formal basis for it in his account of cut-elimination for the sequent calculus, and some provocative philosophical remarks about locating the meaning of logical connectives in their introduction rules within natural deduction.
Portail:Logique. Une page de Wikipédia, l'encyclopédie libre. Ce portail a pour but de présenter la logique qui est un des domaines les plus importants de la recherche et de la connaissance. Category:Logic stubs. Liste de concepts logiques. Un article de Wikipédia, l'encyclopédie libre. Cet article liste les principaux concepts logiques, au sens philosophique du terme, c'est-à-dire en logique générale (issue de la dialectique). Bibliographie de logique et de philosophie du langage. Logique. Un article de Wikipédia, l'encyclopédie libre. Gregor Reisch« La logique présente ses thèmes centraux », Margarita Philosophica, 1503/08 (?). Les deux chiens veritas et falsitas courent derrière le lièvre problema, la logique se presse armée de son épée syllogismus. En bas à gauche se trouve Parménide dans une grotte, grâce auquel la logique aurait été introduite dans la philosophie.
La logique (du grec logikê, dérivé de logos (λόγος), terme utilisé pour la première fois par Xénocrate[1] signifiant à la fois raison, langage, et raisonnement) est dans une première approche l'étude des règles formelles que doit respecter toute argumentation correcte. La logique antique se décompose en dialectique, rhétorique, et théorie de la connaissance [Informations douteuses] [réf. nécessaire] (à rapprocher de l'épistémologie). Логика. Logique mathématique. Introduction à la logique mathématique. Nous avons maintenant tous les outils en main pour réaliser des raisonnements mathématiques complets. Un raisonnement permet d'établir une proposition à partir d'une ou de plusieurs propositions initiales admises (ou précédemment démontrées) en suivant les règles de la logique. Nous allons dans cette dernière partie détailler quatre "types" de raisonnement, quatre "méthodes" pour démontrer une proposition : Trouver un exemple ou un contre-exempleDémontrer la contraposéeRaisonner par l'absurdeRaisonner par récurrence Ces différentes formes de raisonnements devront s'appliquer dans des cas bien particuliers.
Exemple et contre exemple. Les territoires de la logique. Théorie des ensembles de von Neumann–Bernays–Gödel. Un article de Wikipédia, l'encyclopédie libre. La théorie des classes a été introduite en 1925 par John von Neumann, mais celui-ci avait pris comme objets primitifs des fonctions[2]. Théorème de Herbrand. Un article de Wikipédia, l'encyclopédie libre. En logique, le théorème de Herbrand établit un lien entre calcul des prédicats et calcul des propositions. Alors qu'il est possible de déterminer de manière certaine si une proposition du calcul des propositions est démontrable ou pas, la question équivalente pour une formule du calcul des prédicats est plus délicate.
Le théorème de Herbrand répond partiellement à cette question, bien qu'on sache depuis les travaux de Gödel, Tarski, Church, Turing et autres, qu'il n'existe pas d'algorithme permettant de décider si une formule générale du calcul des prédicats est prouvable ou non. Formules prénexes[modifier | modifier le code] Une formule du calcul des prédicats est prénexe si tous les quantificateurs qu'elle contient se trouvent au début de la formule. Autoréférence. Un article de Wikipédia, l'encyclopédie libre. L’autoréférence est la propriété, pour un système, de faire référence à lui-même. Autosimilarité. Un article de Wikipédia, l'encyclopédie libre.
Fractale. Un article de Wikipédia, l'encyclopédie libre. Mise en abyme. Théâtre dans le théâtre. Film contenant un film. Argument circulaire. Formule autoréférente de Tupper. Aporie. Paradoxe. Paradoxes (Jean-Paul Delahaye) Paradoxe de Curry. Paradoxe de Russell. Paradoxe de Hempel. Cercle vicieux. Paradoxe de l'œuf et de la poule. Paradoxe du menteur. Contradiction performative. Pangramme autodescriptif. Sophisme. Totalité. Logique intuitionniste. Constructivisme (mathématiques) Logique linéaire. Calcul des propositions.
Calcul des prédicats. Forme prénexe. Syllogisme. Barbara (syllogisme) Prédicat (logique mathématique) Validité (logique) Déduction naturelle. Modus ponens. Théière de Russell. Théorie des modèles. Ehrenfeucht–Fraïssé game. Skolémisation. Élimination des quantificateurs. Idéographie. Théorèmes d'incomplétude de Gödel. Les théoremes d'incomplétude de Gödel - La tour d'ivoire de John Bonobo. Le théorème de Gödel pour les nuls. Preuve ontologique de Gödel. Incomplétude, Gödel, un aperçu. Logique modale.
Nécessité et contingence. Possibilité et impossibilité. Mondes possibles.