

Babylone. Babylonian Pythagoras - MacTutor History of Mathematics. Pythagoras's theorem in Babylonian mathematics In this article we examine four Babylonian tablets which all have some connection with Pythagoras's theorem.

Certainly the Babylonians were familiar with Pythagoras's theorem. A translation of a Babylonian tablet which is preserved in the British museum goes as follows:- 4 is the length and 5 the diagonal. What is the breadth ? All the tablets we wish to consider in detail come from roughly the same period, namely that of the Old Babylonian Empire which flourished in Mesopotamia between 1900 BC and 1600 BC. Here is a map of the region where the Babylonian civilisation flourished. Babylonian numerals - MacTutor History of Mathematics. The Babylonian civilisation in Mesopotamia replaced the Sumerian civilisation and the Akkadian civilisation.

We give a little historical background to these events in our article Babylonian mathematics. Certainly in terms of their number system the Babylonians inherited ideas from the Sumerians and from the Akkadians. From the number systems of these earlier peoples came the base of 60, that is the sexagesimal system. Yet neither the Sumerian nor the Akkadian system was a positional system and this advance by the Babylonians was undoubtedly their greatest achievement in terms of developing the number system. Some would argue that it was their biggest achievement in mathematics. Often when told that the Babylonian number system was base 60 people's first reaction is: what a lot of special number symbols they must have had to learn. Now although the Babylonian system was a positional base 60 system, it had some vestiges of a base 10 system within it.
Which, in decimal notation is 424000. Babylonian mathematics - MacTutor History of Mathematics. The Babylonians lived in Mesopotamia, a fertile plain between the Tigris and Euphrates rivers.

Here is a map of the region where the civilisation flourished. The region had been the centre of the Sumerian civilisation which flourished before 3500 BC. This was an advanced civilisation building cities and supporting the people with irrigation systems, a legal system, administration, and even a postal service. Writing developed and counting was based on a sexagesimal system, that is to say base 60. Around 2300 BC the Akkadians invaded the area and for some time the more backward culture of the Akkadians mixed with the more advanced culture of the Sumerians. However the Babylonian civilisation, whose mathematics is the subject of this article, replaced that of the Sumerians from around 2000 BC The Babylonians were a Semitic people who invaded Mesopotamia defeating the Sumerians and by about 1900 BC establishing their capital at Babylon. Here is one of their tablets ab=2(a+b)2−a2−b2 Ancient Babylonian mathematics - History Topics - MacTutor History of Mathematics.
Babylone. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Située sur le Tigre et l'Euphrate dans l'ancienne Mésopotamie (du grec meso = entre et potamos = fleuve), Babylone est aujourd'hui à l'état de ruine.

Son nom originel Bab Elli signifie la porte de Dieu, c'est la Babel de la Bible. Bâtie il y a près de 2500 ans à 160 km de Bagdad, capitale de l'actuel Iraq, la nouvelle cité fut la consécration de la civilisation chaldéenne et la source des mathématiques égyptiennes. La ville doit sa puissance aux conquêtes de Nabuchodonosor Ier (vers -1137) puis son éclat, bien plus tard après des périodes de troubles et d'asservissement par les Assyriens, sous le règne de Nabuchodonosor II (vers - 600). Les jardins suspendus, s'ils existèrent (selon Hérodote), dateraient de cette époque et sont classés parmi les sept merveilles du Monde avec : mot clé mésopotamiens » Source Google Earth : La mesure du temps : » Ahmes . RITTAUD YBC7289. Plimpton 322. Histoire et mathématiques : tablette et babyloniens. Proust 2009 za pp. SHM 18/10/2019 - Comment une approche émique des textes mathématiques... - Proust. Tablette YBC 7289.
Le Nouveau Testament rapporte que l’apôtre Paul, s’adressant aux Athéniens, les aurait complimentés pour avoir, sur l’un de leurs autels, rédigé l’inscription : « à un dieu inconnu !
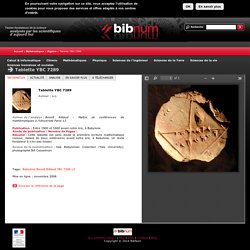
» À la lecture de la tablette babylonienne YBC 7289 (Yale Babylonian Collection), l’on serait bien tenté de dresser aussi un autel à ce mathématicien inconnu qui, il y a près de quatre mille ans, a gravé dans l’argile ce qui est pour nous l’un des plus extraordinaires documents mathématiques qui soit. La tablette YBC 7289 a été rédigée entre 1900 et 1600 avant notre ère. Sa forme ronde et sa taille (environ 8 cm de diamètre) en font un objet facile à tenir en main, ce qui fait probablement d’elle le résultat du travail d’un apprenti.
C’est ainsi que ce qui n’a peut-être été en son temps qu’une simple « copie d’élève » est pour nous un témoignage majeur sur la manière dont les Babyloniens percevaient les mathématiques. Figure 1 : la tablette YBC 7289, et son schéma représentatif à droite an =(an–1+a/an–1)/2. Histoire algo babylone.