

Fractals. OSGOOD (COURBE DE/) cdelahaye, complexités, page 246)PEANO (COURBE DE/)
Une fractale : objet géométrique auto-similaire ou invariant par changement d'échelle - Spécialités. Mandelbrot et définition Une fractale est un objet géométrique auto-similaire ou invariant par changement d'échelle : si on zoome sur une partie de la figure, on retrouve la figure entière.
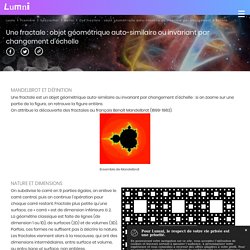
On attribue la découverte des fractales au français Benoît Mandelbrot (1899-1983). Ensemble de Mandelbrot Nature et dimensions On subdivise le carré en 9 parties égales, on enlève le carré central, puis on continue l'opération pour chaque carré restant. La géométrie classique est faite de lignes (de dimension 1 ou 1D), de surfaces (2D) et de volumes (3D). Art et informatique © 1998 Earl L. Les ordinateurs sont de bons outils pour générer des figures fractales. En partenariat avec université paris-sud 11 Paris-Sud est une université pluridisciplinaire à dominante scientifique et de santé. El Árbol de Pitágoras – MatematicasCercanas.
El tan conocido y mencionado en la escuela teorema de Pitágoras establece que en todo triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud del triángulo rectángulo) es igual a la suma de los cuadrados de los catetos (los dos lados menores del triángulo, los que conforman el ángulo recto).

Una forma tradicional de representar dicho teorema es la de la siguiente figura: Podemos plantearlo como que tenemos un cuadrado, y sobre uno de sus lados construimos un triángulo rectángulo, de manera que sobre cada uno de los dos catetos de ese triángulo construimos sendos cuadrados de lado dichos catetos respectivamente. Ahora, con los dos cuadrados construidos posteriormente podemos repetir el mismo procedimiento. Si, por ejemplo, lo repetimos dos veces más, tendríamos algo así: IV TRIANGLE DE SIERPINSKI. Triangle de Sierpinski. Sierpinski Alvarez. Menger. IV Von Koch. Flocon de Koch. Vidéos de présentation de quelques programmes interactifs. Tapis de Sierpinski. Fractales. Fractales. L arbre pythagoricien essai de devoir maison. Hexagone. Beaucoup plus simple. MIAOU. Fractales fiche01 elev.
Fractales fiche02 elev (1) Fractales fiche03 elev. Fractales fiche03 comment (1) Un algorithme fractal. Fractales fiche04 comment. Fractales fiche04 elev. Fractal Casio TI. Fractales à la recherche de la dimension cachée HD part 4/4. Diaporama Fractales - Images de Janet Parke. Fougère. FOUGÈRE DE BARNSLEYBarnsley's fern, Barnsley-Farn Le génie de Barnsley a été de considérer la fougère comme un arbre fractal à 3 branches : Contrairement aux arbres, l'obtention d'une fougère réaliste nécessiterait de pousser jusqu'à une trentaine d'itérations, ce qui est impossible avec des moyens normaux (330 = 2. 1014 segments...).

Le feuillage de la fougère (c'est-à dire l'attracteur des 3 contractions ci-dessus) s'obtient facilement par itération de ces 3 contractions) : Pour faire apparaître les tiges, le "truc" de Barnsley est de prendre une quatrième contraction affine ramenant toute la fougère à son "tronc", de matrice où e est très petit, voir nul et h est la hauteur de la fougère = , ce qui donne ici On peut aussi prendre comme 4ème "contraction" une fonction qui donne un point choisi au hasard dans le segment [AB], ou mieux, dans un rectangle de médiane ce segment, pour obtenir une épaisseur. Voir aussi : © Robert FERRÉOL 2019. Fractales.