

Unraveling biological networks: Biological network motif discovery algorithms. A new approach to disentangling the complexities of biological networks, such as the way in which proteins interact in our body's cells has been developed by researchers in China.
The team's algorithm could allow biologists and biomedical researchers to unravel new clues about how cells work and what goes awry with such networks in various diseases, such as Alzheimer's disease and cancer. New algorithm offers ability to influence systems such as living cells or social networks. At first glance, a diagram of the complex network of genes that regulate cellular metabolism might seem hopelessly complex, and efforts to control such a system futile.
However, an MIT researcher has come up with a new computational model that can analyze any type of complex network -- biological, social or electronic -- and reveal the critical points that can be used to control the entire system. Potential applications of this work, which appears as the cover story in the May 12 issue of Nature, include reprogramming adult cells and identifying new drug targets, says study author Jean-Jacques Slotine, an MIT professor of mechanical engineering and brain and cognitive sciences. Slotine and his co-authors applied their model to dozens of real-life networks, including cell-phone networks, social networks, the networks that control gene expression in cells and the neuronal network of the C. elegans worm.
Unraveling biological networks: Biological network motif discovery algorithms. Unraveling biological networks: Biological network motif discovery algorithms. Algorithm. Flow chart of an algorithm (Euclid's algorithm) for calculating the greatest common divisor (g.c.d.) of two numbers a and b in locations named A and B.
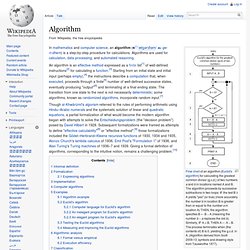
The algorithm proceeds by successive subtractions in two loops: IF the test B ≥ A yields "yes" (or true) (more accurately the numberb in location B is greater than or equal to the numbera in location A) THEN, the algorithm specifies B ← B − A (meaning the number b − a replaces the old b). Similarly, IF A > B, THEN A ← A − B. The process terminates when (the contents of) B is 0, yielding the g.c.d. in A. (Algorithm derived from Scott 2009:13; symbols and drawing style from Tausworthe 1977). In mathematics and computer science, an algorithm (
Visualizing Algorithms. The power of the unaided mind is highly overrated… The real powers come from devising external aids that enhance cognitive abilities.

—Donald Norman Algorithms are a fascinating use case for visualization. To visualize an algorithm, we don’t merely fit data to a chart; there is no primary dataset. Instead there are logical rules that describe behavior. This may be why algorithm visualizations are so unusual, as designers experiment with novel forms to better communicate. List of algorithms. From Wikipedia, the free encyclopedia Jump to navigationJump to search Wikimedia list article.
Step Aside Google Image Search, Here’s an Algorithm that Knows What’s in a Picture. The internet is a wealth of information.
But you have to know what you’re looking for. If you only know a basic category—like that weird looking modern chair at your buddy’s office—not so good. Search modern chair and prepare to be bombarded with general definitions of chairs or the history of chairs or a mishmash of unlabeled chair pictures. Really what you want are all the specific variations of chairs, browsable by image, so you can recognize your target with a quick scan. From there, you can go on to find out its history, inventor, price, and more. Fuzzy Logic Tutorial - An Introduction. Interception of Two Moving Objects in 2D Space. Introduction This information will allow you to determine the direction that an object ("Chaser") must move so that it is able to intercept a target object ("Runner").
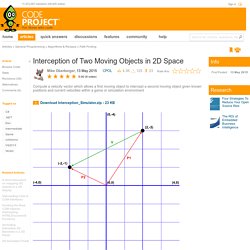
It assumes that you know the positions of both objects in 2D space. It assumes that you know the speed at which your Chaser can move. It assumes that you know the current speed and direction of the Runner. Both the Chaser and the Runner are abstracted to points on a plane. Background. How to Win at Rock-Paper-Scissors. Rock-paper-scissors* isn’t obviously interesting to look at mathematically.
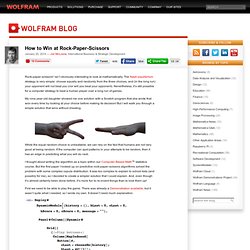
The Nash-equilibrium strategy is very simple: choose equally and randomly from the three choices, and (in the long run) your opponent will not beat you (nor will you beat your opponent). Nevertheless, it’s still possible for a computer strategy to beat a human player over a long run of games. My nine-year-old daughter showed me one solution with a Scratch program that she wrote that won every time by looking at your choice before making its decision! But I will walk you through a simple solution that wins without cheating.
While the equal random choice is unbeatable, we can rely on the fact that humans are not very good at being random. I thought about writing the algorithm as a topic within our Computer-Based Math™ statistics course. First we need to be able to play the game. Random player The code is mostly user interface, display, and game rules. Binary Search Tree Implementation in Java. Workflow Patterns. Downloads of the original and revised control-flow patterns papers: N.

Russell, A.H.M. ter Hofstede, W.M.P. van der Aalst, and N. Mulyar. Workflow Control-Flow Patterns: A Revised View. How to Win at Rock-Paper-Scissors. Opinie > Meningen : Algoritmes Nemen Alles Over. Vrijdag 15 november 2013 | 29 reacties.
Building a Balanced Tree From a List in Linear Time. The usual way of forming a search tree from a list is to scan the list and insert each of its element, one by one, into the tree, leading to a(n expected) run-time of However, if the list is sorted (in ascending order, say) and the tree is not one of the self-balancing varieties, insertion is.