

Esercizi su serie numeriche - Matematica II - ROX @ Unisa - Forum degli studenti di Ingegneria. Materiale didattico per mate 2! - Matematica II - ROX @ Unisa - Forum degli studenti di Ingegneria. Matematicagenerale.it. Logica-matematica.it. Le GUIDE di LOGICA-MATEMATICA.it Le SERIE NUMERICHE sono tra gli esercizi di logica più comuni e più frequenti in molti Concorsi Militari e Pubblici.
Esercizi sulle serie numeriche. Serie e sequenze di numeri. [HOME - BASE Cinque - Appunti di Matematica ricreativa] 0 - 1 - 2 - 3 - 4 - 5 - ...

Come continua questa serie di numeri? 1. Prove d'intelligenza faciliIn alcuni test d'intelligenza si chiede di completare delle serie numeriche. Quasi sempre si tratta di giochi da ragazzi. 2. 3. 4. 5. 6. 7. 8. Ultimo aggiornamento: giugno 2005 Risposte & riflessioni. BASE Cinque - Appunti di Matematica ricreativa. BASE Cinque in Power-Saving Mode Cari amici, BASE Cinque ha bisogno di riposare un po'.
Per un periodo imprecisato di tempo non inserirò nuovi articoli. Il sito tuttavia rimane attivo e tutti i suoi contenuti sono raggiungibili consultando l'archivio o il motore di ricerca interno. Se avete un problema interessante o divertente, non esitate: inviatelo al forum. Pace e bene a tutti! Appunti precedenti. Matematica & Logica. Crescita personale. Unita_3 Le PIRAMIDI di NUMERI. Serie-svolti. Serie piramidale pag. 1/3 - Leggi argomento. Serie piramidale pag. 2/3 - Leggi argomento. Cheguevilla ha scritto: e sottointeso che si cerca la soluzione meno dispendiosa No, non è assolutamente vero.Anzi...
Vabbeh, dici che non importa quanto sia o meno dispendiosa la situazione ma rifiuti lo skate-board, forse è sottointeso che deve trattarsi di un mezzo di trasporto con un numero dispari di ruote Codice: Seleziona tutto Però il discorso è complesso.Comunque, non fa differenza l'ambito. Fa differenza eccome!! Anche ad un colloquio orale, non sarebbe gradita la tua risposta.Perchè mostrerebbe, come già detto, l'incapacità di trovare la soluzione più immediata. Già, ma è meglio così, se per gli organizzatori del colloquio [e^((n-1)/2)] non è immediata evidentemente non si trattava del lavoro che fa per me. Infatti, la risposta di eugenio è efficace: trovare una logica semplice a cui la serie appartiene.
Mi ero promesso di non rispondere, ma per l'ennesima volta mi sono mentito e per farmi perdonare vi lascio questa bella serie ahime da completare 0,1,9,36,100.... Serie piramidale pag. 3/3 - Leggi argomento. Serie. Da Wikipedia, l'enciclopedia libera.
Tra le serie di particolare interesse vi è la serie aritmetica, caratterizzata dal fatto che la differenza tra ciascun termine e il suo precedente è una costante, e la serie geometrica, in cui il rapporto tra ciascun termine e il suo precedente è una funzione costante. Nel caso più generale in cui il rapporto fra termini successivi è una funzione razionale, la serie è detta ipergeometrica. Di particolare importanza in analisi complessa sono le serie di funzioni che sono serie di potenze, come la serie geometrica e la serie di Taylor. Le serie di funzioni costituiscono inoltre efficaci strumenti per lo studio delle funzioni speciali e per la risoluzione di equazioni differenziali.
Definizione[modifica | modifica sorgente] . La somma: Per ogni indice della successione si definisce successione delle somme parziali associata a la somma dei termini della successione. Numero triangolare. Da Wikipedia, l'enciclopedia libera.
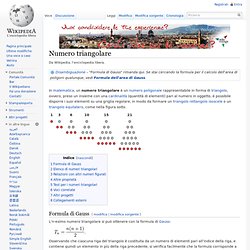
In matematica, un numero triangolare è un numero poligonale rappresentabile in forma di triangolo, ovvero, preso un insieme con una cardinalità (quantità di elementi) pari al numero in oggetto, è possibile disporre i suoi elementi su una griglia regolare, in modo da formare un triangolo rettangolo isoscele o un triangolo equilatero, come nella figura sotto. Formula di Gauss[modifica | modifica sorgente] L'n-esimo numero triangolare si può ottenere con la formula di Gauss: Osservando che ciascuna riga del triangolo è costituita da un numero di elementi pari all'indice della riga, e contiene quindi un elemento in più della riga precedente, si verifica facilmente che la formula corrisponde a quella della somma dei primi.
Serie numeriche, 2nd folder. => Successioni numeriche: consigli UTILI! Test serie numeriche?

Continua a leggere e troverai delle belle dritte! => Test di logica con serie numeriche. I test di logica con le serie numeriche sono, molto probabilmente, fra i quiz di logica più temuti.

A mia esperienza, chi non ha mai avuto un buon rapporto con la matematica ha un sottile moto di terrore quando si tocca l’argomento delle serie numeriche. In realtà, basta investire un po’ di tempo per capire il meccanismo di base di questo genere di test di logica e poi non dico che viene tutto automatico, ma di sicuro la loro risoluzione sarà molto più semplice… In primo luogo è necessario assimilare il quadro teorico, e per questo ti rimando a un mio precedente articolo sulle serie numeriche. Una volta che la teoria sarà salda, il primo sforzo, quando si incontrerà un test di logica con una serie numerica, sarà quello di ricondurre, in base all’attenta osservazione, la successione alla sua opportuna tipologia.
Look-and-say sequence. The lines show the growth of the numbers of digits in the look-and-say sequences with starting points 23 (red), 1 (blue), 13 (violet), 312 (green).
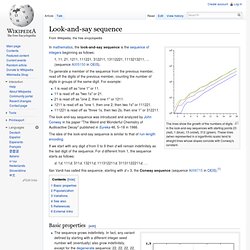
These lines (when represented in a logarithmic scale) tend to straight lines whose slopes coincide with Conway's constant. In mathematics, the look-and-say sequence is the sequence of integers beginning as follows: 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ... (sequence A005150 in OEIS). To generate a member of the sequence from the previous member, read off the digits of the previous member, counting the number of digits in groups of the same digit. Forget Fibonacci! Other Interesting Sequences - Corner Cubicle.
The On-Line Encyclopedia of Integer Sequences® (OEIS®) Costante di Conway. Da Wikipedia, l'enciclopedia libera.
La costante di Conway è una costante matematica legata a un gioco, il decadimento audioattivo. Essa riguarda il tasso di crescita di una stringa di numeri quando ad essa viene applicata la regola del decadimento audioattivo, detta anche guarda e parla: se si trovano n cifre adiacenti uguali ad x, al loro posto si sostituisce nx. Esempio: se si ha una stringa fatta così: al suo posto si sostituisce 32 (sono tre cifre "due").
Poi il procedimento si può ripetere, e al passo successivo si sostituisce la stringa 1312 (un "tre" e un "due"). Ad esclusione del caso in cui il numero di partenza sia 22 (che dà luogo alla sequenza degenere 22, 22, 22, ...), il numero di cifre Ln dell'n-esima stringa è una quantità che cresce al crescere di n. Dove = 1,3035772690342963912570991121525518907307025046594... è chiamata costante di Conway ed è l'unica radice reale positiva dell'equazione Bibliografia[modifica | modifica sorgente] Decadimento audioattivo.