

Les nombres premiers. Le crible d'Eratostène. Paradoxe.

. . . - aucun nombre premier n'est pair sauf un - aucun nombre premier n'est pair sauf deux Le crible Un nombre est dit premier, s'il admet exactement 2 diviseurs distincts (lui-même et l'unité). 1 n'est donc pas premier. PLEIN ECRAN Ce crible, qui permet de trouver tous les nombres premiers jusqu'à un entier spécifié, a été développé par Eratosthène. Les nombres premiers sont connus depuis l'Antiquité mais en dépit de la fascination qu'ils exercent il n'a pas encore été possible de percer leur mystère, c'est-à-dire de savoir s'il existe ou non, une loi de leur formation. Python: nb de nombres premiers inférieurs à n. Cet exercice ainsi que sa correction est proposé par Philippe Moutou.
Il enseigne au lycée Henri IV à Paris. Exercice Écrire une fonction premiers(n) qui détermine la liste des nombres premiers inférieurs ou égaux à un entier n donné. Selon la méthode du crible d’Ératosthène, on peut supprimer d’une liste contenant les entiers entre 2 et n tous les multiples de 2, puis supprimer tous les multiples du nombre suivant 2 (sauf erreur, cela doit être 3), etc. Corrigé La méthode du crible d’Ératosthène est relativement simple à mettre en oeuvre : on parcourt la liste des nombres entiers inférieurs ou égaux à n autant de fois qu’il est possible en supprimant les multiples du premier nombre non supprimé. Les nombres premiers — Science étonnante #34.
L'Hypothèse de Riemann — Science étonnante #62. Les nombres premiers sont-ils (presque) aléatoires ? Actu 2. Le Mystère Des Nombres Premiers. John Tate - The Galileo of Number Theory [Popular presentation] YouTube. 'Experimenting with Primes' - Dr Holly Krieger. Nombre premier. Nombres naturels de zéro à cent.
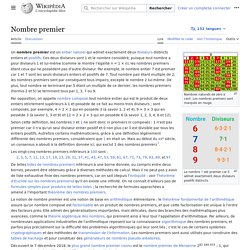
Les nombres premiers sont marqués en rouge. Un nombre premier est un entier naturel qui admet exactement deux diviseurs distincts entiers et positifs. Ces deux diviseurs sont 1 et le nombre considéré, puisque tout nombre a pour diviseurs 1 et lui-même (comme le montre l’égalité n = 1 × n), les nombres premiers étant ceux qui n’en possèdent aucun autre.
Par exemple, le nombre entier 7 est premier car 1 et 7 sont les seuls diviseurs entiers et positifs de 7. Par opposition, on appelle nombre composé tout nombre entier qui est le produit de deux entiers strictement supérieurs à 1 et possède de ce fait au moins trois diviseurs ; sont composés, par exemple, 4 = 2 × 2 qui en possède 3 (à savoir 1, 2 et 4), 9 = 3 × 3 qui en possède 3 (à savoir 1, 3 et 9) et 12 = 2 × 2 × 3 qui en possède 6 (à savoir 1, 2, 3, 4, 6 et 12). Éléments historiques[modifier | modifier le code] Jalons symboliques[modifier | modifier le code] ). Et . Nombres premiers - une introduction et développements complets. The prime numbers are natural numbers, like 2, 3, 5, 7, 11, . . . , which are not multiples of any smaller natural number, except 1.

A prime number is any number whose only factors are 1 and itself. A prime number can be divided evenly only by 1, or itself. And it must be a whole number greater than 1. A prime number (or prime integer, often simply called a "prime" for short) is a positive integer p>1 that has no positive integer divisors other than 1 and p itself.
More concisely, a prime number p is a positive integer having exactly one positive divisor other than 1, meaning it is a number that cannot be factored. – Wolfram MathWorld The Fundamental Theorem of Arithmetic states that every integer n >1 can be represented as a product of primes in only one way, apart from the order of the factors. There are infinitely many prime numbers – Euclid (300 A.C.) The sieve of Eratosthenes – Eratosthenes (275–194 B.C.) Arithmétique/Nombres premiers. Nombres premiers-Décomposition en facteurs premiers. Mathématiques Arithmétique.
Nombres premiers - records. L'estimation du nombre de chiffres en décimal passe par le log base 10 de 2. log base 10 de 2 = 0,3010299957… log base 10 de 10 = 1 En effet, en faisant un petit détour par les logarithmes: 2k en log donne => log ( 2k) = k . log (2) 10p en log donne => log (10p) = p . log (10) = p On cherche la relation entre p et k lorsque 2k = 10p, soit, en égalisant les deux relations ci-dessus:

Les plus grands nombres premiers. Détails Mis à jour : 6 juin 2018 Affichages : 8840 Historique de la recherche du plus grand nombre premier Le record du plus grand nombre premier connu a presque toujours été un nombre premier de Mersenne donc de la forme Mn=2n−1.
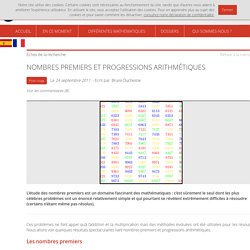
Images des mathématiques. Si on utilise le crible d’Erathostène pour faire la liste des nombres premiers [1], on peut difficilement ne pas remarquer que le nombre de nombres premiers se terminant par un $1$ est à peu près le même que celui des nombres premiers se terminant par un $3$, un $7$ ou un $9$.

On est donc naturellement amené à penser qu’il y a une infinité de nombres premiers de la forme $10n+a$, si $a=1$, $3$, $7$ ou $9$, et plus généralement, qu’il y a une infinité de nombres premiers dans les progressions arithmétiques de la forme $Dn+a$, si $a$ est premier à $D$. Le théorème de la progression arithmétique En adaptant la preuve des grecs de l’existence d’une infinité [2] de nombres premiers, il n’est pas difficile de prouver qu’il en existe une infinité de la forme [3] $4n-1$ ; avec un peu plus de technologie, on montre sans trop de peine qu’il en existe une infinité de la forme [4] $4n+1$.
Le théorème de Tchebotarev Alors, fin de l’histoire ? La conjecture de Sato-Tate Fin de l’histoire ? Images des mathématiques. Les nombres premiers sont les briques élémentaires dans la construction du grand édifice des nombres entiers.

Ils sont caractérisés par la propriété d’être plus grands que 2 (donc 1 n’est pas premier) et de n’être divisibles que par 1 et eux-mêmes. Les premiers de la liste sont $2,3,5,7,11,13,17,...$ N’importe quel nombre s’écrit comme un produit de nombres premiers. Par exemple \[132=2\times2\times3\times 11.\] De plus, cette décomposition est unique (si on écrit les nombres premiers par ordre croissant, par exemple [1]). C’est ce que l’on appelle le théorème fondamental de l’arithmétique et qui était déjà connu en Grèce antique.
Nombres premiers et progressions arithmétiques. Ces problèmes ne font appel qu’à l’addition et la multiplication mais des méthodes évoluées ont été utilisées pour les résoudre.
Nous allons voir quelques résultats spectaculaires liant nombres premiers et progressions arithmétiques. Les nombres premiers Un nombre premier est un entier naturel admettant exactement deux diviseurs distincts, et lui-même. On a l’habitude de noter le -ième nombre premier. Ainsi, La première question sur les nombres premiers fut de savoir si cette suite s’arrête ou continue à l’infini, autrement dit, de savoir s’il existe une infinité de tels nombres. On pourrait être tenté de trouver une formule qui donne le prochain nombre premier connaissant les précédents. Preuve : Posons , le produit de tous les entiers plus petits que . Progressions arithmétiques. Nombres premiers et cryptologie : l’algorithme RSA. Aujourd'hui, en particulier avec le développement d'internet, transmettre des informations confidentielles de façon sécurisée est devenu un besoin primordial...
Aussi, bien qu'il s'agisse d'une science très ancienne, la cryptologie est toujours d'actualité. Les cigales et les nombres premiers. Des cigales qui ont un cycle de 17 ans On a, depuis Jean de la Fontaine, une image un peu ingrate des cigales, qui seraient un insecte insouciant. Pourtant, la partie visible (ou plutôt audible!) De la vie des cigales, ces quelques semaines d'été où elles chantent à tue-tête, ne constitue qu'une petite partie de leur vie. En effet, vers la fin de l'été, les femelles pondent des oeufs dans la moelle des tiges. Ces oeufs, plus d'une centaine par femelle, vont, après incubation, grandir jusqu'à éclore au mois d'octobre, donnant naissance à des larves. Les larves passent plusieurs années dans le sol, en général de deux à cinq ans. Comme mentionné plus haut, la durée d'un cycle de vie pour la plupart des espèces de cigales est de l'ordre de 2 à 5 ans.
Pourquoi 17 ans? Évidemment, le fait que la longueur d'un cycle soit 13 ou 17 ans, et pas 14 ni 16, fait s'interroger les scientifiques. Les nombres 13 et 17 ont la particularité d'être des nombres premiers. L'explication proposée par S. Why do prime numbers make these spirals? Pi hiding in prime regularities. Cours supérieur sur les nombres premiers. Premiers.