

Deuxième ordre amorti. Eléments de Mathématiques. Document 1 " De toutes les sciences de la nature, la physique est celle qui entretient le plus de relations étroites avec les mathématiques, si étroites d’ailleurs que bien des grands noms se retrouvent associés à la fois à des théorèmes mathématiques et à des lois physiques : Descartes, Fermat, Gauss, Bernoulli, ...

Apprendre - Diagonalisation des matrices symétriques réelles. Ce cours est consacré au théorème de diagonalisation des matrices symétriques réelles.

Deux démonstrations sont données : l'une basée entièrement sur le calcul matriciel, avec un minimum de prérequis, l'autre basée sur l'étude vectorielle des opérateurs symétriques dans un espace euclidien. Prérequis : Avoir des connaissances de bases sur la notion de diagonalisation, de forme bilinéaire non dégénérée et une bonne connaissance des espaces euclidiens sont nécessaires. Électricité - Champ électrique créé par un fil rectiligne infini uniformément chargé. 01.pdf. Volume de la sphère. Physagreg : Cours d'électromagnétisme : cours 1 : champ électrostatique. Introduction Qu'est ce que l'électromagnétisme ?
L'interaction électromagnétique est une des quatre interactions fondamentales : ces interactions régissent à elles seules tous les phénomènes physiques de l'univers. Les trois autres interactions connues sont la gravitation (qui se manifeste surtout avec les corps très massiques), l'interaction forte (celle qui assure la cohésion des noyaux des atomes) et l'interaction faible (qui permet notamment les réactions nucléaires). Les interactions fondamentales Alors qu'électricité et magnétisme étaient considérés comme deux phénomènes indépendants, Maxwell, grâce aux travaux de ses prédécesseurs, formalise 4 équations qui les unissent. Thevenin%20Norton%20TD%20complet. Charge et décharge d'un condensateur à travers une résistance.
Cours de mathématiques supérieures. Monter: Calcul intégral précédent: Pratique du Calcul intégral Sous-sections Dans ce (long) chapitre, on montre comment on trouve une primitive pour toute fraction rationnelle , où.
LaTeX Equation Editor for Writing Maths on the Internet. Maths54.free.fr. Maths54.free.fr. Régime de saturation. Ce régime est assez simple à comprendre, c'est pourquoi c'est par celui-là que nous commençons.
Fonctionnement en régime de saturation Pour comprendre le fonctionnement du transistor dans ce fameux régime, il suffit de deux schémas avec le même montage mais un état différent de l'interrupteur : ouvert et fermé. Fiche sur les espaces vectoriels - Stuvia. Cours_electromagnetisme_djelouah.pdf. Microsoft Word - DÉVELOPPEMENTS LIMITÉS 5.doc - Microsoft Word - DÉVELOPPEMENTS LIMITÉS 5.doc - Main.dvi - adc.ps__annexes.maths.pdf. Alpha: Computational Knowledge Engine. Sinus et cosinus hyperbolique. Untitled. Exercices corrigés d'intégration par parties. L'intégration par parties Introduction Cet article explique le mécanisme de l'intégration par parties à travers différents exemples concrets, détaillés et commentés dans le but de trouver la primitive d'une fonction.
Lors de l'illustration du calcul de primitives, de nombreuses astuces seront données pour aller plus vite, certaines astuces permettant même d'éviter parfois l'intégration par parties. Comme pour tous les articles mathématiques du site Gecif.net la vulgarisation mathématique permet ici d'expliquer avec des mots et des notions simples (de niveau BAC) des résultats qui demandent en principe un niveau bien supérieur. Le calcul de dérivées doit être parfaitement connu avant de vouloir effectuer une recherche de primitives par intégration par parties. Notions de base Règles d'écriture adoptées ici. Liste des animations Flash. Le concept de champ. La physique quantique Le concept de champ Dans le cadre de la physique moderne, le concept de champ occupe une place majeure, toute aussi importante par ses conséquences que le quantum d’action.
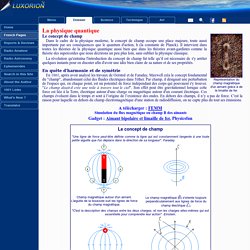
Il intervient dans toutes les théories de la physique quantique aussi bien que dans les théories avantgardistes comme la théorie des supercordes que nous décrirons un peu plus loin, sans oublier la physique classique. Champ et potentiel électrostatiques. Étude des distributions de charges électriques immobiles 1 - Rappels matière <---> atomes <---> noyaux, électrons.

Cours d'électromagnétisme : cours 2 : potentiel et énergie électrostatiques. Introduction Nous allons définir dans ce chapitre une grandeur scalaire intimement lié au champ électrostatique : le potentiel électrostatique.
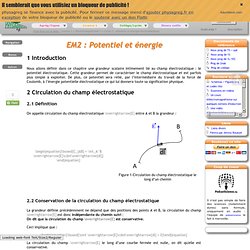
Cette grandeur permet de caractériser le champ électrostatique et est parfois plus simple à exploiter. De plus, ce potentiel sera relié, par l’intermédiaire du travail de la force de Coulomb, à l’énergie potentielle électrostatique ce qui lui donnera toute sa signification physique. Circulation du champ électrostatique Définition On appelle circulation du champ électrostatique \overrightarrow{E} entre A et B la grandeur : \begin{equation}\boxed{C_{AB} = \int_A^B \overrightarrow{E}\cdot\overrightarrow{dl}}\end{equation} Calcul instantané des racines d'un polynôme de degré quelconque. Tableaux et chaînes (cours C et algo) Tableaux Tableaux à une dimension Jusqu'à présent, nous avons manipulé des données uniques dont la valeur pouvait changer (variables) ou ne changeait jamais (constantes).
Logique Formelle. Cours informatique divers : initiation, gestion de projet, etc... Espaces vectoriels de dimensions finies. Académie en ligne : tous les cours de l'année en accès gratuit. Fetch.php. Formule de Moivre et d'Euler. Trigonométrie - GEOME2.PDF. Méthode Maths : cours et exercices de Maths en vidéo. Sommaire Qu'est-ce-qu'un complexe ? Représentation graphiqueModule et argument : forme exponentielleCalcul du module et de l'argumentLien avec le cercle trigonométriqueLe i de la partie imaginaireLe conjuguéFormules à connaîtreQuantité conjuguéeEquation du second degréHomothétie, translation, rotationPoint invariantApplication à la géométrieUne vidéo sur les complexes !
Annales de bac corrigéesIntérêt des complexes Introduction Contrairement à ce que pourrait laisser supposer leur nom, les complexes, c'est pas compliqué ! Le cours est assez simple, mais comme beaucoup de notions se recoupent dans les exercices, il y aura peu d'exercices en vidéo, mais on t'a préparé plein d'annales en vidéo Bon allez, passons aux choses sérieuses ! Qu'est-ce-qu'un complexe ? Un complexe se note souvent z, et s'écrit sous la forme z = a+ib, avec a et b réels, par exemple 3+4i, 5-2i, -8+7i... a est la partie REELLE, tandis que b est ce qu'on appelle la partie IMAGINAIRE. --- Attention ! Représentation graphique. Dérivée d'une fonction composée, et d'une fonction réciproque. Exo7 : Cours et exercices de mathématiques. Des sujets de partiels, des sujets d'examens, des exercices corrigés en vidéos, tout pour réussir sa licence de Mathématiques.
Identités remarquables de degré supérieur à 2. Il s'agit du développement de la somme a+ b à une certaine puissance. Les coefficients des termes sont les nombres du triangle de Pascal. Formulation générale Notation développée (coefficients à la française) Dérivées - Différentielles-Dérivées d'ordre supérieur. Formule de Leibniz.