

amul
Classified
Web Design and Development. Non-Euclidean Geometry. In three dimensions, there are three classes of constant curvature geometries.
All are based on the first four of Euclid's postulates, but each uses its own version of the parallel postulate. The "flat" geometry of everyday intuition is called Euclidean geometry (or parabolic geometry), and the non-Euclidean geometries are called hyperbolic geometry (or Lobachevsky-Bolyai-Gauss geometry) and elliptic geometry (or Riemannian geometry). Spherical geometry is a non-Euclidean two-dimensional geometry. It was not until 1868 that Beltrami proved that non-Euclidean geometries were as logically consistent as Euclidean geometry. Www.math.ucla.edu/~tao/ Dyadic product. Dyadic notation was first established by Josiah Willard Gibbs in 1884.
In this article, upper-case bold variables denote dyadics (including dyads) whereas lower-case bold variables denote vectors. An alternative notation uses respectively double and single over- or underbars. Definitions and terminology[edit] Arithmetization of analysis. The arithmetization of analysis was a research program in the foundations of mathematics carried out in the second half of the 19th century.
Kronecker originally introduced the term arithmetization of analysis, by which he meant its constructivization in the context of the natural numbers (see quotation at bottom of page). The meaning of the term later shifted to signify the set-theoretic construction of the real line. Its main proponent was Weierstrass, who argued the geometric foundations of calculus were not solid enough for rigorous work. Grigori Perelman. Grigori Yakovlevich Perelman (Russian: Григорий Яковлевич Перельман, IPA: [ɡrʲɪˈɡorʲɪj ˈjɑkəvlʲɪvʲɪtʃ pʲɪrʲɪlʲˈman] ( )/ˈpɛrɨlmən/ PERR-il-mən[dubious ]; Russian: Григо́рий Я́ковлевич Перельма́н; born 13 June 1966) is a Russian mathematician who made landmark contributions to Riemannian geometry and geometric topology before his presumed withdrawal from mathematics.
Divergence. In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar.
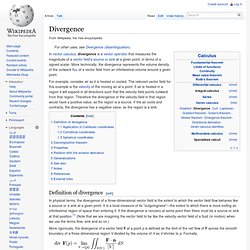
More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point. For example, consider air as it is heated or cooled. The relevant vector field for this example is the velocity of the moving air at a point. If air is heated in a region it will expand in all directions such that the velocity field points outward from that region. Curl (mathematics) The alternative terminology rotor or rotational and alternative notations rot F and ∇ × F are often used (the former especially in many European countries, the latter, using the del operator and the cross product, is more used in other countries) for curl and curl F.
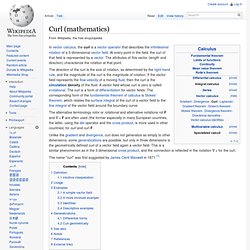
The name "curl" was first suggested by James Clerk Maxwell in 1871.[1] The components of F at position r, normal and tangent to a closed curve C in a plane, enclosing a planar vector areaA = An. The curl of a vector field F, denoted by curl F, or ∇ × F, or rot F, at a point is defined in terms of its projection onto various lines through the point.
If. Riemann,zeta,function. Statistical mechanics: the Riemann zeta function interpreted as a partition function. The Riemann zeta function interpreted as a partition function lattice-related number theory (involving Ising models, percolation, etc.) integer partition problems and physics entropy and number theory number theory and statistical mechanics – general probabilistic number theory.

Analytic continuation. In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function.
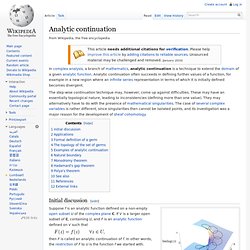
Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which it is initially defined becomes divergent. The step-wise continuation technique may, however, come up against difficulties. These may have an essentially topological nature, leading to inconsistencies (defining more than one value). They may alternatively have to do with the presence of mathematical singularities.
Riemann zeta function. , which converges when the real part of s is greater than 1.
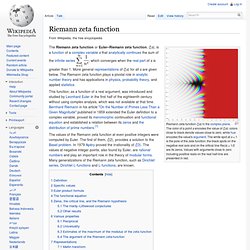
More general representations of ζ(s) for all s are given below. The Riemann zeta function plays a pivotal role in analytic number theory and has applications in physics, probability theory, and applied statistics. Hyperreal number. The system of hyperreal numbers is a way of treating infinite and infinitesimal quantities.
The hyperreals, or nonstandard reals, *R, are an extension of the real numbers R that contains numbers greater than anything of the form Such a number is infinite, and its reciprocal is infinitesimal. The term "hyper-real" was introduced by Edwin Hewitt in 1948.[1] The Tesseract. Wolfram. Mathematics. Field of study Mathematics (from Greek: μάθημα, máthēma, 'knowledge, study, learning') includes the study of such topics as quantity (number theory),[1] structure (algebra),[2] space (geometry),[1] and change (analysis).[3][4][5] It has no generally accepted definition.[6][7] Rigorous arguments first appeared in Greek mathematics, most notably in Euclid's Elements.[10] Since the pioneering work of Giuseppe Peano (1858–1932), David Hilbert (1862–1943), and others on axiomatic systems in the late 19th century, it has become customary to view mathematical research as establishing truth by rigorous deduction from appropriately chosen axioms and definitions.
Mathematics developed at a relatively slow pace until the Renaissance, when mathematical innovations interacting with new scientific discoveries led to a rapid increase in the rate of mathematical discovery that has continued to the present day. History The Babylonian mathematical tablet Plimpton 322, dated to 1800 BC. Etymology. List of theorems. This is a list of theorems, by Wikipedia page. See also Most of the results below come from pure mathematics, but some are from theoretical physics, economics, and other applied fields. 0–9[edit] A[edit] B[edit] C[edit] Theorem. Many mathematical theorems are conditional statements. In this case, the proof deduces the conclusion from the hypotheses. In light of the interpretation of proof as justification of truth, the conclusion is often viewed as a necessary consequence of the hypotheses, namely, that the conclusion is true in case the hypotheses are true, without any further assumptions.
Math resources. Duality. From Wikipedia, the free encyclopedia Duality may refer to: Mathematics[edit] Philosophy, logic, and psychology[edit] Science[edit] Electrical and mechanical[edit] Beauty of Mathematics « Crazy People With Crazy Things. Chronology of Pure and Applied Mathematics. Portal @ MathLinks. MathPages. Category theory « The Unapologetic Mathematician. Comma Categories Another useful example of a category is a comma category. The term comes from the original notation which has since fallen out of favor because, as Saunders MacLane put it, “the comma is already overworked”. We start with three categories.
Category Theory Awodey Course. Www.liegroups.org. ATLAS of Finite Group Representations - V3. Www.liegroups.org. Algebraic structure. Algebraic geometry. Algebraic topology. Cohomology. Abelian Group. Algebraic geometry. Riemannian geometry. Elliptic geometry is also sometimes called "Riemannian geometry". Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length of curves, surface area, and volume. From those some other global quantities can be derived by integrating local contributions. Symplectic geometry. Differential geometry. Non-Euclidean geometry.
Special values of L-functions. John Cremona's home page. Number Theory. Algebraic Topology. Homotopy. The two dashed paths shown above are homotopic relative to their endpoints. The animation represents one possible homotopy. Formal definition[edit] Euler characteristic. Abstract Algebra. Mathematics. Monad (category theory) If and. Orbifold construction of the modes of the Poincare dodecahedral space - Jeffrey Weeks. Logarithmic spiral. Harvard extension school courses. Abstract Algebra - Free Harvard Courses. Algebra. Ring (mathematics) Abstract Algebra - Free Harvard Courses - StumbleUpon. Virtual Training Suite - free Internet tutorials to develop Internet research skills.
The Thirty Greatest Mathematicians. Srinivasa Ramanujan. Carl Friedrich Gauss. Quantum field theory. Adjoint functors. Monad (category theory) Subgroup. Symmetrization. ABSTRACT ALGEBRA: OnLine Study Guide, Table of Contents. Vladimir Voevodsky. Groupoidification. Topology/Homotopy. Topology. Type theory in nLab. Homotopy Type Theory, I. Coherence theorem.