

Relation between Schrödinger's equation and the path integral formulation of quantum mechanics. Background[edit] Schrödinger's equation[edit] Schrödinger's equation, in bra–ket notation, is where is the Hamiltonian operator.
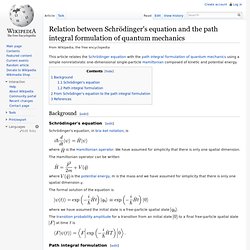
We have assumed for simplicity that there is only one spatial dimension. The Hamiltonian operator can be written is the potential energy, m is the mass and we have assumed for simplicity that there is only one spatial dimension q. The formal solution of the equation is where we have assumed the initial state is a free-particle spatial state The transition probability amplitude for a transition from an initial state to a final free-particle spatial state at time T is Path integral formulation[edit] The path integral formulation states that the transition amplitude is simply the integral of the quantity The reformulation of this transition amplitude, originally due to Dirac[1] and conceptualized by Feynman,[2] forms the basis of the path integral formulation.[3] From Schrödinger's equation to the path integral formulation[edit] The transition amplitude can then be written.
Quantum logic. Quantum logic can be formulated either as a modified version of propositional logic or as a noncommutative and non-associative many-valued (MV) logic.[1][2][3][4][5] Quantum logic has some properties which clearly distinguish it from classical logic, most notably, the failure of the distributive law of propositional logic: p and (q or r) = (p and q) or (p and r), where the symbols p, q and r are propositional variables.
Quantum triviality. In a quantum field theory, charge screening can restrict the value of the observable "renormalized" charge of a classical theory.
If the only allowed value of the renormalized charge is zero, the theory is said to be "trivial" or noninteracting. Thus, surprisingly, a classical theory that appears to describe interacting particles can, when realized as a quantum field theory, become a "trivial" theory of noninteracting free particles. This phenomenon is referred to as quantum triviality. Strong evidence supports the idea that a field theory involving only a scalar Higgs boson is trivial in four spacetime dimensions,[1] but the situation for realistic models including other particles in addition to the Higgs boson is not known in general. Mathematically equivalent formulations of quantum mechanics. Path integral formulation. The path integral also relates quantum and stochastic processes, and this provided the basis for the grand synthesis of the 1970s which unified quantum field theory with the statistical field theory of a fluctuating field near a second-order phase transition.
The Schrödinger equation is a diffusion equation with an imaginary diffusion constant, and the path integral is an analytic continuation of a method for summing up all possible random walks. For this reason path integrals were used in the study of Brownian motion and diffusion a while before they were introduced in quantum mechanics.[3] Einstein–Maxwell–Dirac equations. Einstein–Maxwell–Dirac equations (EMD) are related to quantum field theory.
The current Big Bang Model is a quantum field theory in a curved spacetime. Unfortunately, no such theory is mathematically well-defined; in spite of this, theoreticians claim to extract information from this hypothetical theory. Invariance mechanics. The invariant quantities made from the input and output states of a system are the only quantities needed to give a probability amplitude to a given system.
This is what is meant by the system obeying a symmetry. Since all the quantities involved are relative quantities, invariance mechanics can be thought of as taking relativity theory to its natural limit. Wigner's theorem. Wigner's theorem, proved by Eugene Wigner in 1931,[1] is a cornerstone of the mathematical formulation of quantum mechanics.
The theorem specifies how physical symmetries such as rotations, translations, and CPT act on the Hilbert space of states. According to the theorem, any symmetry acts as a unitary or antiunitary transformation in the Hilbert space. More precisely, it states that a surjective (not necessarily linear) map. Common integrals in quantum field theory. There are common integrals in quantum field theory that appear repeatedly.[1] These integrals are all variations and generalizations of gaussian integrals to the complex plane and to multiple dimensions.
Other integrals can be approximated by versions of the gaussian integral. Fourier integrals are also considered. Scalar field theory. In theoretical physics, scalar field theory can refer to a classical or quantum theory of scalar fields.
A field which is invariant under any Lorentz transformation is called a "scalar", in contrast to a vector or tensor field. The quanta of the quantized scalar field are spin-zero particles, and as such are bosons. The only fundamental scalar field that has been observed in nature is the Higgs field. However, scalar fields appear in the effective field theory descriptions of many physical phenomena. An example is the pion, which is actually a "pseudoscalar", which means it is not invariant under parity transformations which invert the spatial directions, distinguishing it from a true scalar, which is parity-invariant. . , has a particularly simple form: it is diagonal, and here we use the + − − − sign convention. List of quantum field theories. Topological quantum field theory. A topological quantum field theory (or topological field theory or TQFT) is a quantum field theory which computes topological invariants.
Although TQFTs were invented by physicists, they are also of mathematical interest, being related to, among other things, knot theory and the theory of four-manifolds in algebraic topology, and to the theory of moduli spaces in algebraic geometry. Donaldson, Jones, Witten, and Kontsevich have all won Fields Medals for work related to topological field theory. In condensed matter physics, topological quantum field theories are the low energy effective theories of topologically ordered states, such as fractional quantum Hall states, string-net condensed states, and other strongly correlated quantum liquid states. Overview[edit] Local quantum field theory. Let Mink be the category of open subsets of Minkowski space M with inclusion maps as morphisms. We are given a covariant functor from Mink to uC*alg, the category of unital C* algebras, such that every morphism in Mink maps to a monomorphism in uC*alg (isotony).
(Poincaré covariance). Local quantum field theory. Axiomatic quantum field theory. Axiomatic quantum field theory is a mathematical discipline which aims to describe quantum field theory in terms of rigorous axioms. It is strongly associated with functional analysis and operator algebras, but has also been studied in recent years from a more geometric and functorial perspective.
There are two main challenges in this discipline. Constructive quantum field theory. Attempts to put quantum field theory on a basis of completely defined concepts have involved most branches of mathematics, including functional analysis, differential equations, probability theory, representation theory, geometry, and topology. It is known that a quantum field is inherently hard to handle using conventional mathematical techniques like explicit estimates. This is because a quantum field has the general nature of an operator-valued distribution, a type of object from mathematical analysis. The existence theorems for quantum fields can be expected to be very difficult to find, if indeed they are possible at all. Form factor (quantum field theory) For example, at low energies the interaction of a photon with a nucleon is a very complicated calculation involving interactions between the photon and a sea of quarks and gluons, and often the calculation cannot be done.
Often in this context, form factors are also called "structure functions", since they can be used to describe the structure of the nucleon. However the general form of the interaction is known, where represents the photon momentum (equal to E/c, where E is the energy of the photon). Wheeler–Feynman absorber theory. The Wheeler–Feynman absorber theory (also called the Wheeler–Feynman time-symmetric theory) is an interpretation of electrodynamics derived from the assumption that the solutions of the electromagnetic field equations must be invariant under time-reversal symmetry, as are the field equations themselves. Indeed, there is no apparent reason for the time-reversal symmetry breaking which singles out a preferential time direction and thus makes a distinction between past and future. A time-reversal invariant theory is more logical and elegant.
Another key principle, resulting from this interpretation and reminiscent of Mach's principle due to Tetrode, is that elementary particles are not self-interacting. This immediately removes the problem of self-energies. This theory is named after its originators, the late physicists Richard Feynman and John Archibald Wheeler. T-symmetry and causality[edit] Supersymmetry. Multivalued gauge transformations. Gauge theory. Haag's theorem. Haag's theorem. Rudolf Haag postulated [1] that the interaction picture does not exist in an interacting, relativistic quantum field theory (QFT), something now commonly known as Haag's Theorem. Haag's original proof was subsequently generalized by a number of authors, notably Hall and Wightman,[2] who reached the conclusion that a single, universal Hilbert space representation does not suffice for describing both free and interacting fields.
In 1975, Reed and Simon proved [3] that a Haag-like theorem also applies to free neutral scalar fields of different masses, which implies that the interaction picture cannot exist even under the absence of interactions. Renormalization. Renormalization. Axiomatic approaches. Particle conservation and non-conservation. Physical meaning of particle indistinguishability. Unification of fields and particles. Dynamics. Second Quantization. Field operators. Boson. In quantum mechanics, a boson (/ˈboʊsɒn/,[1] /ˈboʊzɒn/[2]) is a particle that follows Bose–Einstein statistics. Bosons make up one of the two classes of particles, the other being fermions.[3] The name boson was coined by Paul Dirac[4] to commemorate the contribution of the Indian physicist Satyendra Nath Bose[5][6] in developing, with Einstein, Bose–Einstein statistics—which theorizes the characteristics of elementary particles.[7] Examples of bosons include fundamental particles such as photons, gluons, and W and Z bosons (the four force-carrying gauge bosons of the Standard Model), the recently discovered Higgs boson, and the hypothetical graviton of quantum gravity; composite particles (e.g. mesons and stable nuclei of even mass number such as deuterium (with one proton and one neutron, mass number = 2), helium-4, or lead-208[Note 1]); and some quasiparticles (e.g.
Cooper pairs, plasmons, and phonons).[8]:130 Types[edit] Properties[edit] Pauli exclusion principle. Fermion. Antisymmetric wavefunction for a (fermionic) 2-particle state in an infinite square well potential. Second quantization. Quantum hydrodynamics. Quantum electrodynamics. First quantization. Single and many-particle Quantum mechanics. Lagrangian formalism. Classical field theory. Classical and Quantum fields. Photon polarization. Symmetry in quantum mechanics. Static forces and virtual-particle exchange.
Geometrodynamics. Quantum field theory in curved spacetime. Quantum field theory. Introduction to quantum mechanics. What is Quantum Physics. Quantum mechanics. "SPOOKY" QUANTUM BIOLOGY. EINSTEIN and BLACK HOLES. INSIDE BLACK HOLES. BIRD: QUANTUM ENTENGLEMENT. RADIUS of BLACK HOLES. QUANTUM EFFECTS. Entenglement + Superposition. ISSUE of COHERENCE. Supersolidity loses its luster. Northwestern University & the Psi’ence of Presentiment. Physicists May Have Evidence Universe Is A Computer Simulation.
Einstein to shed light on black holes. Wormhole. Weird Science. Weird Science (Part 2) Quantum "spooky action at a distance" travels at least 10,000 times faster than light. Controversial quantum computer aces entanglement tests - physics-math - 08 March 2013. Breaking the Speed of (Light) Thought. So you think YOU'RE confused about quantum mechanics? Scientists await new worlds as CERN collider is refitted. Back to the Future 2 – Here We Come. Entropy law linked to intelligence, say researchers. Nothing to see: The man who made a Majorana particle - opinion - 13 May 2013.
Vortex to another dimension reported in Brighton. Researcher teleports with a kitten. Quantum Puzzles: Funny Things Happen When Space And Time Vanish : 13.7: Cosmos And Culture. The True Science of Parallel Universes. Time Travel: What is the most mind boggling example of a time travel paradox. Time Travel: Which paradox comes most close to support the possibility of Time Travel. Www.mta.ca/~rhudson/papers/turku.htm. Weird Quantum Tunneling Enables 'Impossible' Space Chemistry. If this theory is correct, we may live in a web of alternate timelines.
Is The Universe A Hologram? Physicists Say It's Possible. Simulations back up theory that Universe is a hologram. Quantum black hole study opens bridge to another universe. Is Earth Weighed Down By Dark Matter, Or Internet? #3 Parallel Worlds exist and will soon be testable, expert says.
The Quantum Mechanics of Fate - Issue 9: Time. Scientific Research Suggests We Unconsciously React to Events Up to 10 Seconds Before They Happen. Predicting the unpredictable: Critical analysis and practical implications of predictive anticipatory activity. How To Change The Past. Discovery of Quantum Vibrations in 'Microtubules' Inside Brain Neurons Supports Controversial Theory of Consciousness. The Sacred, Spherical Cows of Physics - Issue 13: Symmetry. Best Explanation of Quantum Field Theory That You Will Ever Hear, Provided by Sean Carroll in Less than 2 Minutes at the 46th Annual Fermilab Users Meeting. Wormhole Photon Time Travel - Casimir Energy, Messages. Scientific Research Suggests We Unconsciously React to Events Up to 10 Seconds Before They Happen.
The Quantum Mechanics of Fate - Issue 9: Time.