

Le nombre d'or - Micmaths. LE NOMBRE D'OR VU PAR LES BIOLOGISTES ET PAR LES EGYPTIENS. Le magazine National Géographique publie une petite vidéo sur le nombre d’or.

Le regard des biologistes est intéressant, ces derniers voient dans le nombre d’or un principe universel d’ordre mathématique pour organiser le vivant. D’ailleurs, la chose est curieuse, car le logo du magazine National Géographique est un rectangle d’or. Les anciens avaient ils compris cela depuis plusieurs millénaires ? Nature by Numbers - Cristóbal Vila (2010) Les plantes et l'arithmétique. Le nombre d'or. Golden Fractal Tree with Python Turtle (Source Code) – Python and Turtle. Golden Dragon Curve Fractal (Source Code) – Python and Turtle. Nombre d'or et abeilles. Le nombre d’or ou “divine proportion”représente parait-il le rapport le plus esthétiquement parfait que l’on puisse trouver dans la nature, dans les monuments antiques, les œuvres d’art célèbres ou un simple rectangle.
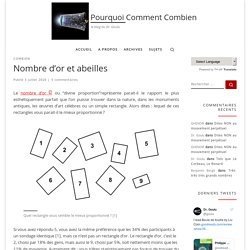
Alors dites : lequel de ces rectangles vous parait-il le mieux proportionné ? Si vous avez répondu 5, vous avez la même préférence que les 34% des participants à un sondage identique [1], mais ce n’est pas un rectangle d’or. Le rectangle d’or, c’est le 2, choisi par 18% des gens, mais aussi le 9, choisi par 5%, soit nettement moins que les 11% de moyenne. Autrement dit : vous n’êtes statistiquement pas foutus de trouver du divin dans un rectangle… Ce fameux “nombre d’or” Φ est défini historiquement comme le rapport de deux nombres a et b satisfaisant l’équation . Dévoilons les Maths 4 : Math et Art. Le nombre d'or - Automaths #05. Mathématiques : Comment le « nombre d’or » a influencé les Arts (et quelques instagrameurs) Le nombre d’or, nommé aussi proportion divine, dicte un rapport harmonieux entre les différentes parties d’un objet ou d’une image.
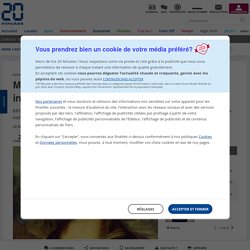
Le mathématicien Étienne Ghis, dans un article du Monde rappelle ainsi que : Lorsqu’on décompose un objet en deux parties inégales, on dit que la proportion est divine, ou dorée, si le rapport entre la grande partie et la petite est le même que le rapport entre le tout et la grande partie. On le représente par le nombre φ phi (fi) et a un lien direct avec le nom du sculpteur grec Phidias à l’origine de la façade du Parthénon d’Athènes. Sa valeur est de 1,61803398874989482045… résultat d’une équation mathématique connue depuis la Grèce antique, à savoir (1 +√5)/2.
LE NOMBRE D’OR FUT-IL LE PREMIER DES IRRATIONNELS ? Avez-vous déjà entendu parler du nombre d’or ?

Très probablement. Comment le définissez-vous ? Le nombre d'Or, la beauté mesurée. Calcul de cos(2π/5) = 1/2 Phi et pentagone régulier. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges A - 2π/5 est la mesure en radians de l'angle au centre interceptant un côté du pentagone régulier.
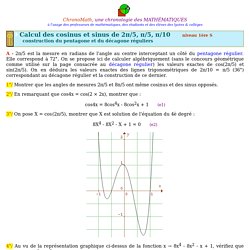
Elle correspond à 72°. Le nombre d'or. L' histoire ...

Il y a 10 000 ans : Première manifestation humaine de la connaissance du nombre d'or (temple d'Andros découvert sous la mer des Bahamas). 2800 av JC : La pyramide de Khéops a des dimensions qui mettent en évidence l'importance que son architecte attachait au nombre d'or. Vè siècle avant J-C. (447-432 av.JC) : Le sculpteur grec Phidias utilise le nombre d'or pour décorer le Parthénon à Athènes, en particulier pour sculpter la statue d'Athéna Parthénos .
Il utilise également la racine carrée de 5 comme rapport. Concevoir des courbes fractales avec une symétrie de rotation quintuple à l'aide du nombre d'or complexe (anglais) Suite de Fibonacci et nombre d'or - 1ère partie - maths et nature - #Fibonacci #nombre d'or #science. LE NOMBRE D’OR. Le 2 septembre 2019 - Ecrit par Fernando Corbalán Cet article a été écrit en partenariat avec L’Institut Henri Poincaré Lire l'article en En 2013, l’Institut Henri Poincaré et Images des Mathématiques ont uni leurs efforts pour superviser la réédition de la collection Le monde est mathématique, publiée par RBA en partenariat avec Le Monde.
Réveillons le nombre d'or. "Une droite est dite coupée en extrême et moyenne raison quand,comme elle est toute entière relativement au plus grand segment,ainsi est le plus grand relativement au plus petit.

" [Euclide, Eléments, livre VI, 3ème définition] Ainsi parla Euclide, et déjà, à l'époque, personne n'avait vraiment compris ce qu'il avait voulu dire. Depuis, de nombreux mathématiciens se sont penchés sur le sujet, et finalement, il parlait de ça : Un segment ayant ses proportions a/b et c/a égales.
Pomme de pin, ananas, tournesol, marguerite, cactus... De l'autre côté du miroir (et ce que Euclide y a trouvé) Le plus doré de tous les nombres. Démystification de Fibonacci. Futura Sciences. Une Nature en Or. Nautile, nombre d’or et spirale dorée. On donne souvent la forme de la coquille du nautile comme exemple d’une spirale dorée.

Mais qu’en est-il exactement? Nombre d’or Le nombre d’or est le rapport obtenu en divisant un segment de droite en extrême et moyenne raison. Voici comment effectuer cette division. TOURNESOL 1ereS. Nombre d'or. La première série de gradins du théâtre d'Épidaure a 34 gradins, la seconde en a 21 : leur rapport 34/21 est une valeur approchée du nombre d'or.
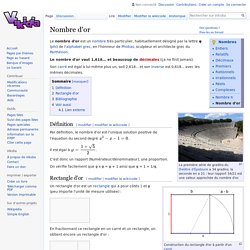
Le nombre d'or est un nombre très particulier, habituellement désigné par la lettre φ (phi) de l'alphabet grec, en l'honneur de Phidias, sculpteur et architecte grec du Parthénon. Le nombre d'or vaut 1,618... et beaucoup de décimales (ça ne finit jamais). Son carré est égal à lui-même plus un, soit 2,618... et son inverse est 0,618... avec les mêmes décimales. Définition[modifier | modifier le wikicode] Spirale d'or. Dessinons une spirale de Fibonacci. Tout le monde connait la célèbre suite de Fibonacci et sa spirale. Cette spirale est composée d’une série de quarts de cercles s’inscrivant chacun dans un carré. Ces carrés sont disposés selon un chemin qui tourne autour du centre de la spirale et recouvrent entièrement rectangle tendant à être d’or lorsque le nombre de carrés augmente. Messing around with the golden rectangle.
Plantes, spirales et nombres. Plantes, spirales et nombres. Le nombre d or. Le nombre d'or. Ce site utilise des cookies pour faciliter votre navigation, obtenir des statistiques de visite, et afficher des publicités personnalisées. En savoir plus Le nombre d'or est le nombre irrationnel : c'est-à-dire à peu près 1,6180339... C'est une des deux racines (la plus grande) de l'équation x2-x-1=0. Exprimé comme cela, c'est bien peu de choses pour un nombre qui a acquis, bien au-delà de son intérêt mathématique propre, une dimension architecturale, poétique voire même mystique!
Racine 2 et Nombre d or géom. Cathédrale gothique et nombre d'or, mythe ou réalité. La géométrie spéculative a ses jeux, ses inutilités, comme les autres sciences. Châteaubriant Dans la page précédente, j'ai invalidé la pertinence des seules mathématiques dans l'analyse des tracés gothiques. NOMBRE D OR et CATHEDRALE DE METZ v2017. Polygones 2015. C'est pas sorcier - Batisseurs de cathédrales. Nombre d'or. Autre construction 3.d. Corde et tangente égales. Autour du rectangle d’or. Icosaèdre et rectangles d'or. Suites et TI-92. (terminale S, d'après Gérard Kuntz, Strasbourg) Une histoire couple de lapins qui donnent naissance à un couple d'animaux qui à la génération suivante donne naissance à un nouveau couple et ainsi de suite… (livre de l'abaque «Liber Abaci» de Léonard de Pise dit Fibonacci paru en 1202) Soit la suite de Fibonacci :
[LP#2] Partie entière et nombre d'or. TPE : Le nombre d'or dans la nature, ou et pourquoi ? Le nombre d'or dans la peinture, l'architecture et la nature. Le nombre plastique. Histoire des Arts 2015 : La Joconde et le Nombre d'Or - Collège Les Amandiers. LE NOMBRE D'OR - atelier portrait pastel aquarelle visages dessin regard.
Le nombre d'or. Les boîtes magiques. Jean Fouquet - Arrêt sur : l'art de géométrie. Spirales végétales, le nombre d'or dans les plantes (Fibonacci et fractions continues) Le Nombre d'Or - biologie-nature. Ananas nombre d'or. SEMIGROUPES NUMÉRIQUES ET NOMBRE D’OR (I) SEMIGROUPES NUMÉRIQUES ET NOMBRE D’OR (II) Icosaèdre et rectangles d'or. De l’ordre au désordre. Le nombre d’or. L'origine du NOMBRE D'OR. Le NOMBRE D'OR dans les logos, l'architecture… Nombre d'or : marchés financiers et beauté. Python et le nombre d'or - Mathweb.fr. A Golden Logarithmic Equation. Can you simplify? « Bâtir avec les Nombres... Et le Sacré se Crée ! » avec Christophe Ogi - NURÉA TV.
Nombre d'or. Melekeelloumi. Suite de Fibonacci et nombre d'or. Fibonacci, un mathématicien voyageur - Fermat Science. Suites de Lucas et Fibonacci et Nombre d'or (selon Vincent Thill) Fibonacci & cie... Le nombre d'or et la suite de Fibonacci. Le nombre d'or : Fibonacci (1175-1250) Tuto Maths & Cuisine : Fibonacci et le nombre d'or - Micmaths. UNE SOLUTION EN OR ! Pour chercher et approfondir - Dans l’œil de la spirale d’or.
Spirales. Histoire des arts. Le nombre d'or.