

G Spencer-Brown: Laws of Form. Www.math.ucla.edu/~tao/ UV Displacement Comparison. Hammack Home. This book is an introduction to the standard methods of proving mathematical theorems.

It has been approved by the American Institute of Mathematics' Open Textbook Initiative. Also see the Mathematical Association of America Math DL review (of the 1st edition), and the Amazon reviews. The second edition is identical to the first edition, except some mistakes have been corrected, new exercises have been added, and Chapter 13 has been extended. (The Cantor-Bernstein-Schröeder theorem has been added.) The two editions can be used interchangeably, except for the last few pages of Chapter 13. Order a copy from Amazon or Barnes & Noble for $13.75 or download a pdf for free here. Part I: Fundamentals Part II: How to Prove Conditional Statements Part III: More on Proof Part IV: Relations, Functions and Cardinality Thanks to readers around the world who wrote to report mistakes and typos!
Instructors: Click here for my page for VCU's MATH 300, a course based on this book. Stokes' theorem. This classical statement, as well as the classical Divergence theorem, fundamental theorem of calculus, and Green's Theorem are simply special cases of the general formulation stated above.
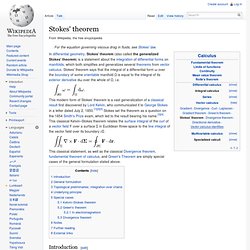
Introduction[edit] Fundamental theorem of calculus. The first part of the theorem, sometimes called the first fundamental theorem of calculus, is that an indefinite integral of a function[1] can be reversed by differentiation.

This part of the theorem is also important because it guarantees the existence of antiderivatives for continuous functions.[2] The second part, sometimes called the second fundamental theorem of calculus, is that the definite integral of a function can be computed by using any one of its infinitely many antiderivatives. This part of the theorem has key practical applications because it markedly simplifies the computation of definite integrals. History[edit] The fundamental theorem of calculus relates differentiation and integration, showing that these two operations are essentially inverses of one another. Geometric meaning[edit] The area shaded in red stripes can be estimated as h times f(x). Curl (mathematics) The alternative terminology rotor or rotational and alternative notations rot F and ∇ × F are often used (the former especially in many European countries, the latter, using the del operator and the cross product, is more used in other countries) for curl and curl F.
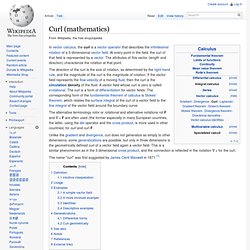
The name "curl" was first suggested by James Clerk Maxwell in 1871.[1] The components of F at position r, normal and tangent to a closed curve C in a plane, enclosing a planar vector areaA = An. The curl of a vector field F, denoted by curl F, or ∇ × F, or rot F, at a point is defined in terms of its projection onto various lines through the point. If. Divergence. In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar.
More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point. For example, consider air as it is heated or cooled. Www.math.ucla.edu/~tao/resource/general/131ah.1.03w/week1.pdf. Dodecahedron.gif (429×204) Honeycomb.gif (250×250) Grigori Perelman. Grigori Yakovlevich Perelman (Russian: Григорий Яковлевич Перельман, IPA: [ɡrʲɪˈɡorʲɪj ˈjɑkəvlʲɪvʲɪtʃ pʲɪrʲɪlʲˈman] ( )/ˈpɛrɨlmən/ PERR-il-mən[dubious ]; Russian: Григо́рий Я́ковлевич Перельма́н; born 13 June 1966) is a Russian mathematician who made landmark contributions to Riemannian geometry and geometric topology before his presumed withdrawal from mathematics.
In 1994, Perelman proved the soul conjecture. In 2003, he proved Thurston's geometrization conjecture. Imaginary number. An imaginary number bi can be added to a real number a to form a complex number of the form a + bi, where a and b are called, respectively, the real part and the imaginary part of the complex number.
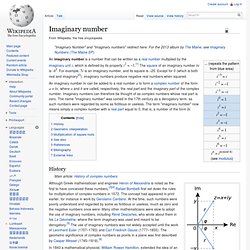
Imaginary numbers can therefore be thought of as complex numbers whose real part is zero. The name "imaginary number" was coined in the 17th century as a derogatory term, as such numbers were regarded by some as fictitious or useless. The term "imaginary number" now means simply a complex number with a real part equal to 0, that is, a number of the form bi. History. Riemann zeta function. , which converges when the real part of s is greater than 1.
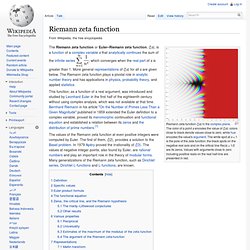
More general representations of ζ(s) for all s are given below. The Riemann zeta function plays a pivotal role in analytic number theory and has applications in physics, probability theory, and applied statistics. This function, as a function of a real argument, was introduced and studied by Leonhard Euler in the first half of the eighteenth century without using complex analysis, which was not available at that time. Euler's formula. This article is about Euler's formula in complex analysis.
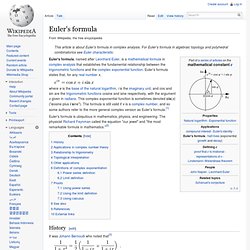
For Euler's formula in algebraic topology and polyhedral combinatorics see Euler characteristic. Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number x, Euler's formula is ubiquitous in mathematics, physics, and engineering. The physicist Richard Feynman called the equation "our jewel" and "the most remarkable formula in mathematics History[edit] It was Johann Bernoulli who noted that[3] Proof of Euler's Identity. List of mathematical symbols. When reading the list, it is important to recognize that a mathematical concept is independent of the symbol chosen to represent it.
For many of the symbols below, the symbol is usually synonymous with the corresponding concept (ultimately an arbitrary choice made as a result of the cumulative history of mathematics), but in some situations a different convention may be used. For example, depending on context, the triple bar "≡" may represent congruence or a definition. Further, in mathematical logic, numerical equality is sometimes represented by "≡" instead of "=", with the latter representing equality of well-formed formulas. In short, convention dictates the meaning. Each symbol is shown both in HTML, whose display depends on the browser's access to an appropriate font installed on the particular device, and in TeX, as an image. Guide[edit] This list is organized by symbol type and is intended to facilitate finding an unfamiliar symbol by its visual appearance. Basic symbols[edit] Arithmetization of analysis. The arithmetization of analysis was a research program in the foundations of mathematics carried out in the second half of the 19th century.
Kronecker originally introduced the term arithmetization of analysis, by which he meant its constructivization in the context of the natural numbers (see quotation at bottom of page). The meaning of the term later shifted to signify the set-theoretic construction of the real line. Its main proponent was Weierstrass, who argued the geometric foundations of calculus were not solid enough for rigorous work. Dyadic product. Dyadic notation was first established by Josiah Willard Gibbs in 1884. In this article, upper-case bold variables denote dyadics (including dyads) whereas lower-case bold variables denote vectors. An alternative notation uses respectively double and single over- or underbars. Definitions and terminology[edit] Dyadic, outer, and tensor products[edit] Www.dpmms.cam.ac.uk/~wtg10/2cultures.pdf.
Karl's Calculus Tutor: 1.0 Number Systems. Calculus deals with properties of the real numbers. In order to understand calculus you must first understand what it is about the real numbers that separates them from other kinds of numbers we use from day to day. FFTW Home Page. Sean Gourley on the mathematics of war. Тензор. Тензор механического напряжения второго ранга. Компоненты тензора в трёхмерной декартовой системе координат образуют матрицу столбцами которой являются силы, действующие на , и грани куба. Часто тензор представляют как многомерную таблицу , заполненную числами — компонентами тензора (где Тензор обычно обозначают некоторой буквой с совокупностью верхних (контрвариантных) и нижних (ковариантных) индексов: . Определения[править | править исходный текст] Современное определение[править | править исходный текст] Тензор ранга над.