

Understanding the Fibonacci Sequence and Golden Ratio. Nature, The Golden Ratio and Fibonacci Numbers. Plants can grow new cells in spirals, such as the pattern of seeds in this beautiful sunflower.
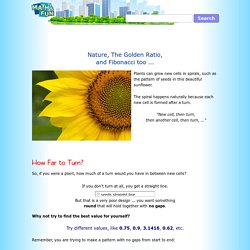
The spiral happens naturally because each new cell is formed after a turn. "New cell, then turn, then another cell, then turn, ... " How Far to Turn? So, if you were a plant, how much of a turn would you have in between new cells? Why not try to find the best value for yourself? Try different values, like 0.75, 0.9, 3.1416, 0.62, etc. Remember, you are trying to make a pattern with no gaps from start to end: (By the way, it doesn't matter about the whole number part, like 1. or 5. because they are full revolutions that point us back in the same direction.)
What Did You Get? If you got something that ends like 0.618 (or 0.382, which is 1 − 0.618) then "Congratulations, you are a successful member of the plant kingdom! " Why? Any number that is a simple fraction (example: 0.75 is 3/4, and 0.95 is 19/20, etc) will, after a while, make a pattern of lines stacking up, which makes gaps. Golden Ratio. The Idea Behind It Have a try yourself (use the slider): Beauty This rectangle has been made using the Golden Ratio, Looks like a typical frame for a painting, doesn't it?
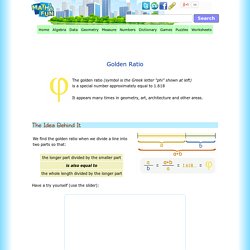
Some artists and architects believe the Golden Ratio makes the most pleasing and beautiful shape. Do you think it is the "most pleasing rectangle"? Maybe you do or don't, that is up to you! Fibonacci Sequence. Fractal Foundation Online Course - Chapter 11 - FIBONACCI FRACTALS. The Golden Ratio The Fibonacci Sequence appears in many seemingly unrelated areas.

In this section we'll see how the Fibonacci Sequence generates the Golden Ratio, a relationship so special it has even been called "the Divine Proportion. " Remember that the next number in the Fibonacci Sequence is just made by adding the current number in the sequence to the number before it. Let's see how the numbers in the Fibonacci Sequence compare to each other. In particular, how much bigger is any Fiboncci number than the one before it? Let's look now at the ratio of successive Fibonacci Numbers, or The ratio of the successive Fibonacci Numbers gets closer and closer to a certain value as n gets larger and larger. Golden ratio. Golden ratio. List of fractals by Hausdorff dimension. Deterministic fractals[edit] Random and natural fractals[edit] See also[edit] Notes and references[edit]
Julia set. Three-dimensional slices through the (four-dimensional) Julia set of a function on the quaternions.
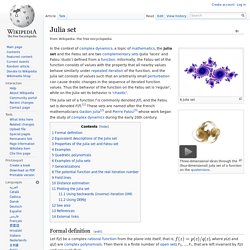
The Julia set of a function f is commonly denoted J(f), and the Fatou set is denoted F(f).[1] These sets are named after the French mathematicians Gaston Julia[2] and Pierre Fatou[3] whose work began the study of complex dynamics during the early 20th century. Formal definition[edit] Let f(z) be a complex rational function from the plane into itself, that is, , where p(z) and q(z) are complex polynomials. Then there is a finite number of open sets F1, ..., Fr, that are left invariant by f(z) and are such that: Koch snowflake. The first seven iterations in animation Zooming into the Koch curve The Koch snowflake (also known as the Koch star and Koch island[1]) is a mathematical curve and one of the earliest fractal curves to have been described.
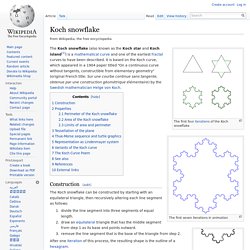
It is based on the Koch curve, which appeared in a 1904 paper titled "On a continuous curve without tangents, constructible from elementary geometry" (original French title: Sur une courbe continue sans tangente, obtenue par une construction géométrique élémentaire) by the Swedish mathematician Helge von Koch. Construction[edit] The Koch snowflake can be constructed by starting with an equilateral triangle, then recursively altering each line segment as follows: divide the line segment into three segments of equal length.draw an equilateral triangle that has the middle segment from step 1 as its base and points outward.remove the line segment that is the base of the triangle from step 2.
En.wikipedia. Fractal art is a form of algorithmic art created by calculating fractal objects and representing the calculation results as still images, animations, and media.
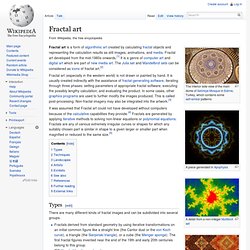
Fractal art developed from the mid-1980s onwards.[1] It is a genre of computer art and digital art which are part of new media art. The Julia set and Mandelbrot sets can be considered as icons of fractal art.[2] Fractal art (especially in the western world) is not drawn or painted by hand. It is usually created indirectly with the assistance of fractal-generating software, iterating through three phases: setting parameters of appropriate fractal software; executing the possibly lengthy calculation; and evaluating the product.
In some cases, other graphics programs are used to further modify the images produced. Types[edit] A 3D Mandelbulb fractal generated using Visions of Chaos There are many different kinds of fractal images and can be subdivided into several groups.