

Youtube.
Pythagorean theorem. The GMAT's Favorite Triangles - Magoosh GMAT Blog. Triangles - SAT Math. Explanation: Because PA and PB are tangent to circle O, angles PAO and PBO must be right angles; therefore, triangles PAO and PBO are both right triangles.
Since AO and OB are both radii of circle O, they are congruent. Furthermore, because PA and PB are external tangents originating from the same point, they must also be congruent. So, in triangles PAO and PBO, we have two sides that are congruent, and we have a congruent angle (all right angles are congruent) between them. Therefore, by the Side-Angle-Side (SAS) Theorem of congruency, triangles PAO and PBO are congruent. Notice that quadrilateral PAOB can be broken up into triangles PAO and PBO. Triangles - High School Math. If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below.
If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors. Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org. Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights.
Geometry: Similar Triangles - Magoosh Math. What is meant when someone says similar triangles?
The next video in our Geometry series addresses this question, and more. Now we can talk about similar triangles. Recall the idea of congruence. If shapes are congruent, it means they have the same shape and the same size. So for example, these are two congruent shapes. The corresponding sides have equal length, the corresponding angles are equal, they’re exactly the same shape just in different orientations. The second one is a smaller copy of the first one, and again it’s in a different orientation. SAT Math Basics – Triangles - Magoosh High School Blog.
What you need to know about triangles on the SAT is nowhere near as much as you probably learned in high school.
Remember law of cosines? Exactly, most people do not. But the law of cosines, and just about every thing else from trigonometry, is not tested on the SAT. Ahh…I think I just heard an audible collective sigh of relief. While the SAT only tests basics aspects of triangles, it will try to trick you whenever possible. 1. 2. 3. Geometry: Triangles - I - Magoosh Math. In Geometry you need to learn a lot about triangles!
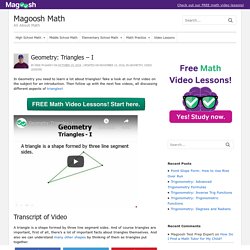
Take a look at our first video on the subject for an introduction. Then follow up with the next few videos, all discussing different aspects of triangles! A triangle is a shape formed by three line segment sides. GMAT Math: Area of a Triangle - Magoosh GMAT Blog. As you may remember from high school, , where b is the base and h is the height.
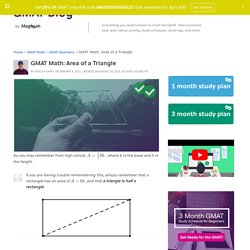
If you are having trouble remembering this, simply remember that a rectangle has an area of , and that a triangle is half a rectangle. Practice Question: Using the Area Formula. New SAT Math: Similar and Congruent Triangles. Because triangles have so many interesting properties that build upon each other, you can count on seeing them on the new SAT.
Although the problems that you will encounter won’t necessarily be difficult, the key lies in being able to figure out which property or concept to use in order to get to the answer. Here you will be tested on figuring out missing side lengths, and you’ll have to brush up on some triangle knowledge before we begin: Re-thinking Pythagoras: Is a triangle obtuse? - Magoosh GMAT Blog. The Pythagorean Theorem is one of the most remarkable theorems in all of mathematics.
It has a treasure trove of ramifications up its sleeve, any one of which could provide you with invaluable help on the GMAT Quantitative section. For example, consider this practice problem. GMAT Math: How do You Find the Height of a Triangle? If you have a right triangle and are given two sides and would like to find the third, use the Pythagorean Theorem: .
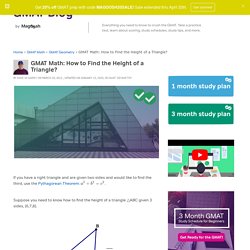
Suppose you need to know how to find the height of a triangle given 3 sides, {6,7,8}. This is a question some GMAT test takers ask. They know they would need the height to find the area, so they worry: how would I find that height. The short answer is: fuhgeddaboudit! Trigonometry: SOHCAHTOA and Special Triangles - Magoosh Math. In our last trigonometry video, we discussed SOHCAHTOA.
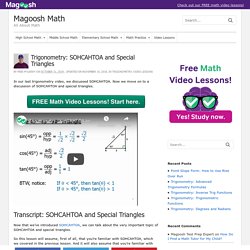
Now we move on to a discussion of SOHCAHTOA and special triangles. Now that we’ve introduced SOHCAHTOA, we can talk about the very important topic of SOHCAHTOA and special triangles. So this lesson will assume, first of all, that you’re familiar with SOHCAHTOA, which we covered in the previous lesson. And it will also assume that you’re familiar with the idea of the special right triangles. What Is an Isosceles Triangle? - Magoosh Math.
Known as the “Father of Geometry,” mathematician Euclid lived around 300 BC. He came up with the rules involving isosceles triangles. 02 Triangles Part I Magoosh GRE. Right triangle word problems — Basic example. Right triangle word problems — Harder example.