

Transactional interpretation. More recently, he has also argued TIQM to be consistent with the Afshar experiment, while claiming that the Copenhagen interpretation and the many-worlds interpretation are not.[3] The existence of both advanced and retarded waves as admissible solutions to Maxwell's equations was explored in the Wheeler–Feynman absorber theory.

Cramer revived their idea of two waves for his transactional interpretation of quantum theory. While the ordinary Schrödinger equation does not admit advanced solutions, its relativistic version does, and these advanced solutions are the ones used by TIQM. Cramer uses TIQM in teaching quantum mechanics at the University of Washington in Seattle. Advances over previous interpretations[edit] The transactional interpretation has similarities with the two-state vector formalism (TSVF)[5] which has its origin in work by Yakir Aharonov, Peter Bergmann and Joel Lebowitz of 1964.[6][7] Recent developments[edit] Debate[edit] TIQM faces a number of common criticisms. 1. 2. 3.
Stochastic interpretation. The stochastic interpretation is an interpretation of quantum mechanics.
The modern application of stochastics to quantum mechanics involves the assumption of spacetime stochasticity, the idea that the small-scale structure of spacetime is undergoing both metric and topological fluctuations (John Archibald Wheeler's "quantum foam"), and that the averaged result of these fluctuations recreates a more conventional-looking metric at larger scales that can be described using classical physics, along with an element of nonlocality that can be described using quantum mechanics.
A stochastic interpretation of quantum mechanics due to persistent vacuum fluctuations is suggested by Roumen Tsekov. The main idea is that vacuum (or spacetime) fluctuations are the reason for quantum mechanics and not a result of it how it is usually considered. See also[edit] References[edit] Edward Nelson (1966). Relational quantum mechanics. This article is intended for those already familiar with quantum mechanics and its attendant interpretational difficulties.

Quantum logic. Quantum logic can be formulated either as a modified version of propositional logic or as a noncommutative and non-associative many-valued (MV) logic.[1][2][3][4][5] Quantum logic has some properties which clearly distinguish it from classical logic, most notably, the failure of the distributive law of propositional logic: p and (q or r) = (p and q) or (p and r), where the symbols p, q and r are propositional variables.
To illustrate why the distributive law fails, consider a particle moving on a line and let p = "the particle has momentum in the interval [0, +1/6]" Objective collapse theory. Objective collapse theories are an approach to the interpretational problems of quantum mechanics.

They are realistic, indeterministic and reject hidden variables. The approach is similar to the Copenhagen interpretation, but more firmly objective. The most well-known examples of such theories are: Compared to other approaches[edit] Collapse theories stand in opposition to many-worlds interpretation theories, in that they hold that a process of wavefunction collapse curtails the branching of the wavefunction and removes unobserved behaviour.
Many-worlds interpretation. The quantum-mechanical "Schrödinger's cat" paradox according to the many-worlds interpretation.
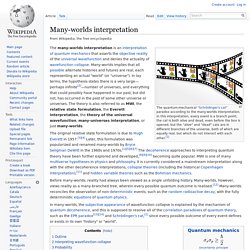
In this interpretation, every event is a branch point; the cat is both alive and dead, even before the box is opened, but the "alive" and "dead" cats are in different branches of the universe, both of which are equally real, but which do not interact with each other.[1] The many-worlds interpretation is an interpretation of quantum mechanics that asserts the objective reality of the universal wavefunction and denies the actuality of wavefunction collapse.
Many-worlds implies that all possible alternate histories and futures are real, each representing an actual "world" (or "universe"). In lay terms, the hypothesis states there is a very large—perhaps infinite[2]—number of universes, and everything that could possibly have happened in our past, but did not, has occurred in the past of some other universe or universes.
Hidden variable theory. Albert Einstein, the most famous proponent of hidden variables, objected to the fundamentally probabilistic nature of quantum mechanics,[1] and famously declared "I am convinced God does not play dice".[2] Einstein, Podolsky, and Rosen argued that "elements of reality" (hidden variables) must be added to quantum mechanics to explain entanglement without action at a distance.[3][4] Later, Bell's theorem would suggest (in the opinion of most physicists and contrary to Einstein's assertion) that local hidden variables of certain types are impossible.

Ensemble interpretation. The ensemble interpretation, or statistical interpretation of quantum mechanics, is an interpretation that can be viewed as a minimalist interpretation; it is a quantum mechanical interpretation that claims to make the fewest assumptions associated with the standard mathematical formalization.

At its heart, it takes to the fullest extent the statistical interpretation of Max Born for which he won the Nobel Prize in Physics.[1] The interpretation states that the wave function does not apply to an individual system – or for example, a single particle – but is an abstract mathematical, statistical quantity that only applies to an ensemble of similarly prepared systems or particles. Copenhagen interpretation. The Copenhagen interpretation is one of the earliest and most commonly taught interpretations of quantum mechanics.[1] It holds that quantum mechanics does not yield a description of an objective reality but deals only with probabilities of observing, or measuring, various aspects of energy quanta, entities that fit neither the classical idea of particles nor the classical idea of waves.
The act of measurement causes the set of probabilities to immediately and randomly assume only one of the possible values. This feature of mathematics is known as wavefunction collapse. The essential concepts of the interpretation were devised by Niels Bohr, Werner Heisenberg and others in the years 1924–27. According to John Cramer, "Despite an extensive literature which refers to, discusses, and criticizes the Copenhagen interpretation of quantum mechanics, nowhere does there seem to be any concise statement which defines the full Copenhagen interpretation.
Background[edit] Consistent histories. In quantum mechanics, the consistent histories approach is intended to give a modern interpretation of quantum mechanics, generalising the conventional Copenhagen interpretation and providing a natural interpretation of quantum cosmology.[1] This interpretation of quantum mechanics is based on a consistency criterion that then allows probabilities to be assigned to various alternative histories of a system such that the probabilities for each history obey the rules of classical probability while being consistent with the Schrödinger equation.

In contrast to some interpretations of quantum mechanics, particularly the Copenhagen interpretation, the framework does not include "wavefunction collapse" as a relevant description of any physical process, and emphasizes that measurement theory is not a fundamental ingredient of quantum mechanics. Histories[edit] A homogeneous history (here labels different histories) is a sequence of Propositions. De Broglie–Bohm theory. The de Broglie–Bohm theory, also known as the pilot-wave theory, Bohmian mechanics, the Bohm or Bohm's interpretation, and the causal interpretation, is an interpretation of quantum theory. In addition to a wavefunction on the space of all possible configurations, it also includes an actual configuration, even when unobserved.