

Múltiplos del número Pi que pretenden ser enteros. Representación del símbolo del número pi y de sus primeras cifras. / getty Con motivo del Día de Pi, EL PAÍS quiere lanzar un desafío a sus lectores.
Este número, conocido como la constante matemática que representa la razón entre el perímetro de una circunferencia y su diámetro, esconde todavía muchos misterios pero los matemáticos saben desde hace muchos años que ningún múltiplo entero de Pi es un entero. Sin embargo hay múltiplos de Pi que se aproximan bastante. El número pi no es 3,14. El 20 de noviembre de 2005, mientras una patera con 10 personas a bordo desaparecía frente a las costas de Cádiz, mientras una tormenta tropical dejaba 11 muertos en Honduras, mientras el tenista suizo Roger Federer perdía su primer partido tras ganar 24 finales consecutivas, el chino Chao Lu recitaba números sin parar.
Durante 24 horas y cuatro minutos, grabado por 26 cámaras y con decenas de testigos de la Universidad de Agricultura y Ciencias Forestales del Noroeste, en la provincia china de Shaanxi, Chao Lu cantó de memoria 67.890 decimales del número pi. Su hazaña fue certificada por el Libro Guinness de los records. No falló ni uno. “Cuando alguien escribe que pi es igual a 3,14 me lloran los ojos”, confiesa el matemático Javier Cilleruelo, asombrado por los enigmas milenarios que oculta el número.
Matejuegos. Grupo CIMAT. Servicios.educarm.es/portal/admin/webForm.php?aplicacion=EDUCARM_MUNDO_MATEMATICO&mode=visualizaAplicacionWeb&web=158&ar=1112&liferay=1&zona=EDUCARM. Lugar geométrico - Problema 6. Enseñanza y aprendizaje digital en el aula de Infantil y Primaria: enlances de apoyo. Repositorios de objetos de aprendizaje. RECURSOS Y MATERIALES DIDÁCTICOS EN EDUCACIÓN MATEMÁTICA. Se incluyen aquí documentos y, en algunos casos, plantillas para la construcción casera de los materiales didácticos más usuales.

En el contenido de este bloque se han tenido en cuenta los trabajos previos de los profesores D. Antonio Ortiz Villarejo, D. Alfonso Ortiz Comas, D. Jesús Gallardo Romero, coordinador de un curso de verano sobre este mismo tema en la Facultad de Ciencias de la Educación, y D. Juan Jesús Larrubia Martínez, autor del material puzzle algebraico. En los apartados dedicados a cursos y a la formación de Maestros y Profesores se completa la información con otras actividades y orientaciones didácticas y se incluyen otros materiales y recursos --------------------- general -----------------
Informaciones de interés > Congreso TALIS Instituto Nacional de Evaluación Educativa. Está usted en: Congreso TALIS (Estudio Internacional de la Enseñanza y el Aprendizaje) Resultados del último Informe TALIS El objetivo del estudio TALIS de la OCDE es ofrecer información sobre los procesos educativos a través de encuestas a profesores y directores de centros educativos.

Este congreso está dirigido al conjunto de profesionales de la educación, inspectores, red de formación del profesorado, investigadores, universidades dedicadas a la formación de futuros profesores y especialmente a los participantes en el estudio TALIS 2013 en ambas modalidades, TALIS y TALIS – PISA Link. Programa Retransmisión vía streaming: Organizan: Instituto Nacional de Evaluación Educativa (INEE), Instituto Nacional de Tecnologías Educativas y de Formación del Profesorado (INTEF) y Consejo Escolar del Estado. Fechas: 25 y 26 de junio. Lugar: Salón de actos de la sede del Ministerio de Educación, Cultura y Deporte. Vídeo presentación de Andreas Schleichers Documentos con los resultados del Informe TALIS: Para saber más, resolver problemas - Ven x más. Serapio García Cuesta y Juan Emilio García Jiménez Se ha dicho que los problemas son oportunidades para demostrar lo que se sabe.

Es por eso que en esta Unidad de trabajo, te vamos a proponer problemas que has de tomar como un reto, un desafío a tus buenas capacidades para las Matemáticas. Te vamos a ayudar mostrándote técnicas y estrategias útiles para avanzar por el apasionante arte de resolver problemas. Enfrentarás los problemas que te vamos a proponer discutiendo con tus compañeros, con la ayuda de los recursos que te vamos a proporcionar y la guía de tu profesor.
Te pedimos confianza en tus propias capacidades, ganas de afrontar retos y desafíos, gusto por la originalidad y creatividad, espíritu reflexivo y perseverancia en la búsqueda de soluciones. Confiamos en que al final de este tiempo quieras venir por más problemas que es lo mismo que venir por más matemáticas. Ampliación del punto de Fermat según un estudio del profesor José Manuel Arranz San José del Centro de Profesores y Recursos de Ponferrada. Mesut Özil y el punto de Fermat. Geometría y fútbol. Algunos habrán pensado que Özil debe colocarse encima de la línea que une a Cristiano Ronaldo y Di María.
Otras personas contestarán que deberá colocarse en el baricentro (intersección de las medianas o centro de gravedad) del triángulo isósceles formado por los otros 3 jugadores. Otros pensarán que deberá situarse en el circuncentro (centro de la circunferencia circunscrita, que pasa por los tres vértices del triángulo), en el incentro (centro de la circunferencia inscrita, tangente a los lados del triángulo), o incluso en el ortocentro (punto de intersección de las alturas). Pero ninguna de estas soluciones es correcta. El resultado lo deberemos hallar de otra forma.
Veamos cómo: Tenemos a Alonso (A), Cristiano (C) y Di María (D) situados en el campo de la siguiente forma: Situamos ahora a Özil (Ö) en un punto cualquiera de la altura del triángulo, ya que según las instrucciones de Mourinho, debe estar delante de Alonso y en el centro del campo: Y también conocemos que ÖC = ÖD. Dibujo Técnico con TIC para Educación Secundaria y Bachillerato. Problemas Matemáticos: Cuatro puntos. RÚBRICAS O MATRICES DE EVALUACIÓN_ PROIDEAC.
En la Comunidad Canaria ya se habla en la Etapa de Primaria del sistema de evaluación por rúbricas.
El curso pasado en Intercentros y a través de la formación que proporciona este espacio, dentro de la Educación de Personas Adultas, pudimos asistir a una de estas formaciones sobre tareas,CCBB y rúbricas. A través del EPA VIRTUAL, elaboramos tareas y rúbricas o matrices de evaluación. Sin lugar a dudas, constituyen una forma de evaluar muy objetiva que cada vez se impone en las diferentes etapas. En Primaria han llegado, y la Consejería dispone de un plan formativo a través de la propia página para que los profesores se puedan ir familiarizando, ya que desde la aplicación pincel, se propone este tipo de evaluación.
¿Qué son las rúbricas? En las celdas de intercección entre categorías a evaluar y calificadores se expresa qué características tendrá la tarea para merecer la calificación correspondiente. Te invito a probar esta aplicación o recurso, al que puedes acceder picando en la imagen: PORTAFOLIO: RÚBRICA PARA EVALUAR EL PORTAFOLIO. CRITERIOS PARA EVALUAR UN PORTAFOLIO. Historia1imagen.files.wordpress.com/2013/03/taller-nc2ba-4-entrega-del-portafolio-digital.pdf. Experto‹6› Www.mauriciocontreras.es/JUEGOS5.pdf. Revistacaparra.juntaextremadura.net/11/archivos/06.pdf. Www.lavirtu.com/eniusimg/enius4/2010/03/adjuntos_fichero_409193_2e49e82db1acac8e.pdf. Herramientas de autor. Mecanismos en un procesador geométrico. Frecuentemente el tema del movimiento surge en el estudio de la geometría, especialmente en el de las transformaciones isométricas, sin embargo este, como dijera en alguna ocasión Hans Freudenthal, es objeto de estudio de la mecánica, más que de la geometría.

En este post me refiero a algunas dificultades para representar el movimiento físico en un procesador geométrico, y a las principales causas, que están directamente vinculadas con la naturaleza del concepto de movimiento para la geometría. Algunos años atrás estuve dándole vueltas al tema de los mecanismos, de lo cuál surgieron algunas construcciones del Mecanismo de Theo Jansen. En aquel entonces me sorprendió un hecho curioso: en determinadas circunstancias, un mecanismo se traba, dado que sus piezas no pueden estirarse más, sin embargo, en un procesador geométrico la misma situación lleva en realidad a que las piezas en cuestión “desaparezcan”. Microsoft Word - Libro de preguntas.doc - doc_31_07_08_5_42_02.pdf. Suma de enteros con Scratch. Este es un pequeño ejemplo de actividad de sumas de enteros programada con Scratch.
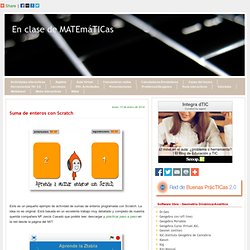
La idea no es original. Está basada en un excelente trabajo muy detallado y completo de nuestra querida compañera Mª Jesús Casado que podéis leer, descargar y practicar paso a paso en la red desde la página del MIT. Está publicado y documentado junto a otros 246 recursos de Matemáticas en SCratchEd. En este espacio podéis encontrar cantidad de ejemplos de los que todos podemos aprender, pequeños y mayores. CPALMS.org. Edu Apps. Curriculum. Edit in Dashboard Designer.
Iesgabrielgalanm.juntaextremadura.net/web/docinterno/protocolos/202000-Instrucciones-programaciones.pdf. Geometría con Cabri II. Mecan/Mecan/Abiblio/GuiaMecan.pdf. Personal.us.es/raufalgan/geogebra_archivos/Sesion.pdf. Www.geogebra.es/intergeo_09/10 Losada/cursillo_avanzado.pdf. Gg_day/comunicaciones/escribano.pdf. Planimeter. Matematicas Visuales. Google Maps Area Calculator Tool. Output : Current Area 0 m² 0 km² 0 acres 0 hectare 0 square feet 0 square nautical miles. Geogebramad - Unidad didáctica 17. Papiroflexia Matemática Introducción Desarrollo de habilidades y valores: Percepción:Tamaño y escalas. Utilizando diversas medidas de papel en figuras o modulares.Composición: combinando elementos de diversa o similar naturaleza para producir efectos complejos. Transición del plano al espacio: la educación transcurre normalmente en el plano, donde escribimos, dibujamos, etc. Definición e Historia de la Papiroflexia.
Luz Manuel Santos Trigo - Documat. Ir al contenido Luz Manuel Santos Trigo Esta página recoge referencias bibliográficas de materiales disponibles en los fondos de las Bibliotecas que participan en Documat. En ningún caso se trata de una página que recoja toda la producción bibliográfica de un autor de manera exhaustiva. Nos gustaría que los datos aparecieran de la manera más correcta posible, de manera que si detecta algún error en la información que facilitamos, puede hacernos llegar su Sugerencia / Errata. Propuesta didáctica la identificación en la resolución de problemas de geometría plana para matemáticas II en nivel de preparatoria - 1020125527.PDF. Www.uam.es/proyectosinv/estalmat/ReunionCantabria2012/Andalucia-Geometria. Thales.cica.es/sites/thales.cica.es.geogebra/files/II_Jornadas_GeoGebra/material/talleres/construyendogeogebra/cuadernillo.pdf. Www.uam.es/personal_pdi/ciencias/ehernan/10-11MasterFPS/Geometria-4-2.
Upload Manager. Proyecto: La Articulación entre la Escuela Media y la Universidad. Unvm.galeon.com/Libro1.pdf. Www.jupenoma.es/secretosgg/02_CAS/doc/PrimerosPasos_CASGG.pdf. Los secretos de GeoGebra. Www.educa.madrid.org/cms_tools/files/aff968f3-b283-40ff-acc3-e4a9880f854a/wiris_4_polinom.pdf. MOGEA - Índice de Agrega. Biblioteca.ucm.es/tesis/edu/ucm-t25694.pdf. Bootstrap. BdelaCalle_1.pdf. Cursotallercienciasimm.wikispaces.com/file/view/MultiplicacionConLineas.pdf. Herramientas, recursos y servicios educativos para profesores.
Imperio de la Ciencia. Entre otras cosas, los matemáticos se dedican a resolver, crear y demostrar cosas. Hoy quiero hablarles de uno de los métodos más poderosos que hay para demostrar, la reducción al absurdo, una técnica milenaria que ya usaban maestros como Arquímedes y Euclides. ¿Cómo funciona la reducción al absurdo? Es muy sencillo. Supongan que quieren demostrar una proposición. Lo que hacemos al reducir al absurdo es suponer que es cierto lo contrario, y a partir de ahí, ir trabajando con las cosas que eso implica para encontrar una contradicción.
En fin para no hacerlos más bolas vamos a ver algunos ejemplos muy padres: 1) El ajedrez de jugada doble tiene las mismas reglas que el ajedrez normal, con la excepción de que cada jugador puede hacer uno o dos movimientos seguidos. Intentar resolver este problema buscando la estrategia que se menciona sería una tarea brutalmente imposible. En el ajedrez de jugada doble, el primer jugador tiene una estrategia no perdedora. Resolución de problemas - Matemáticas en tu mundo. Resolución de problemas - Matemáticas en tu mundo.