

Diagrams. 1.
Introduction Diagrams or pictures probably rank among the oldest forms of human communication. They are not only used for representation but can also be used to carry out certain types of reasoning, and hence play a particular role in logic and mathematics. However, sentential representation systems (e.g., first-order logic) have been dominant in the modern history of logic, while diagrams have largely been seen as only of marginal interest. Diagrams are usually adopted as a heuristic tool in exploring a proof, but not as part of a proof.[1] It is a quite recent movement among philosophers, logicians, cognitive scientists and computer scientists to focus on different types of representation systems, and much research has been focussed on diagrammatic representation systems in particular.
We have the following goals for this entry. 2. The dominance of sentential representation systems in the history of modern logic has obscured several important facts about diagrammatic systems. Archangel Gabriel and Hope - Angels of the Ascension Flame of Purity. Gabriel and Hope are archangel and archeia of the fourth ray of the resurrection and the ascension flame.
Together with the angels of purity and the seraphim, these twin flames guard the immaculate concept of the God design for every man, woman and child upon the planet. Diagrams. Redirect Notice. Google Image Result for. Aristotle's Logic. 1.
Introduction Aristotle’s logical works contain the earliest formal study of logic that we have. It is therefore all the more remarkable that together they comprise a highly developed logical theory, one that was able to command immense respect for many centuries: Kant, who was ten times more distant from Aristotle than we are from him, even held that nothing significant had been added to Aristotle’s views in the intervening two millennia. Organon. The Organon (Greek: Ὄργανον, meaning "instrument, tool, organ") is the standard collection of Aristotle's six works on logic.
The name Organon was given by Aristotle's followers, the Peripatetics. Deductive and Inductive Arguments. Modus ponens. In propositional logic, modus ponens (/ˈmoʊdəs ˈpoʊnɛnz/; MP; also modus ponendo ponens (Latin for "mode that affirms by affirming")[1] or implication elimination) is a rule of inference.[2] It can be summarized as "P implies Q and P are both asserted to be true, therefore Q must be true.
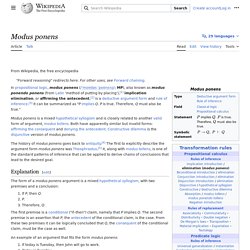
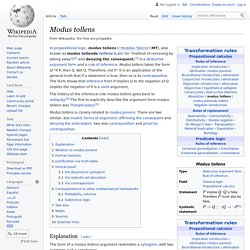
" Modus ponens is closely related to another valid form of argument, modus tollens. Both have apparently similar but invalid forms such as affirming the consequent, denying the antecedent, and evidence of absence. Modus tollens. The inference rule modus tollens validates the inference from implies and the contradictory of to the contradictory of The modus tollens rule can be stated formally as: where stands for the statement "P implies Q".
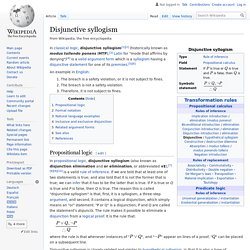
Hypothetical syllogism. Disjunctive syllogism. An example in English:
Categorical Syllogism. Preface One needs the necessary knowledge in order to make the correct decisions.
Likewise, one needs the necessary logic skills, in order to make a correct reasoning. Aristotle is one of the forefathers of modern Logic and Philosophy. Ancient Logic. 1. Pre-Aristotelian Logic 1.1 Syntax and Semantics Some of the Sophists classified types of sentences (logoi) according to their force. So Protagoras (485–415 BCE), who included wish, question, answer and command (Diels Kranz (DK) 80.A1, Diogenes Laertius (D.
Hypothetical syllogism. An example in English: If I do not wake up, then I cannot go to work.
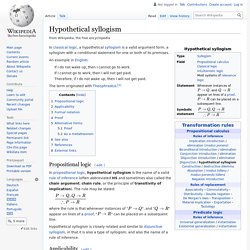
If I cannot go to work, then I will not get paid. Therefore, if I do not wake up, then I will not get paid. The term originated with Theophrastus.[1] Definition of Premise by Merriam-Webster. Syllogistically. Predication. English[edit] Etymology[edit] Middle English predicacion, from Anglo-Norman predicaciun, from Latin praedicātiō, from praedicō.
Noun[edit] predication (countable and uncountable, plural predications) A proclamation, announcement or preaching.An assertion or affirmation. quotations ▼1965 June 4, Shigeyuki Kuroda, “Generative grammatical studies in the Japanese language”, in DSpace@MIT[1], retrieved 2014-02-24:It can be immediately observed from these sentences that the English subject of a predication is translated in Japanese with a wa-phrase, while the subject of a nonpredicational description appears as a ga-phrase.
Translations[edit] See also[edit] prediction References[edit] OED 2nd edition 1989. Definition of Predication by Merriam-Webster. Aristotle on Non-contradiction. 1. Three Versions of the Principle of Non-Contradiction There are arguably three versions of the principle of non-contradiction to be found in Aristotle: an ontological, a doxastic and a semantic version.
The first version concerns things that exist in the world, the second is about what we can believe, and the third relates to assertion and truth. The first version (hereafter, simply PNC) is usually taken to be the main version of the principle and it runs as follows: “It is impossible for the same thing to belong and not to belong at the same time to the same thing and in the same respect” (with the appropriate qualifications) (Metaph IV 3 1005b19–20). The following are some of those qualifications: The “same thing” that belongs must be one and the same thing and it must be the actual thing and not merely its linguistic expression. History of logic. Reductio ad impossibile. Proof of a proposition which involves demonstrating that its negation entails a contradiction; since a contradiction cannot be true, whatever ... Access to the complete content on Oxford Reference requires a subscription or purchase.
Public users are able to search the site and view the abstracts and keywords for each book and chapter without a subscription. Reductio ad Hitlerum. Reductio ad Hitlerum (/ˈhɪtlərəm/; pseudo-Latin for "reduction to Hitler"; sometimes argumentum ad Hitlerum, "argument to Hitler", ad Nazium, "to Nazism"), or playing the Nazi card, is an attempt to invalidate someone else's position on the basis that the same view was held by Adolf Hitler or the Nazi Party,[1] for example: "Hitler was against tobacco smoking, X is against tobacco smoking, therefore X is a Nazi".
Coined by Leo Strauss in 1953, reductio ad Hitlerum borrows its name from the term used in logic, reductio ad absurdum (reduction to the absurd).[2] According to Strauss, reductio ad Hitlerum is a form of ad hominem, ad misericordiam, or a fallacy of irrelevance. The suggested rationale is one of guilt by association. It is a tactic often used to derail arguments, because such comparisons tend to distract and anger the opponent, as Hitler and Nazism have been condemned in the modern world.[3] Fallacious nature[edit]
Aristotle's organon. Assertoric. Hegelianism. Hegelianism is the philosophy of G. W. F. Hegel which can be summed up by the dictum that "the rational alone is real",[1] which means that all reality is capable of being expressed in rational categories. His goal was to reduce reality to a more synthetic unity within the system of absolute idealism. Method[edit] Dialectic. Assertoric. Vernacular. Common speech variety of a specific population. Circular reasoning. Formal fallacy. While a logical argument is a non sequitur if, and only if, it is invalid, the term "non sequitur" typically refers to those types of invalid arguments which do not constitute formal fallacies covered by particular terms (e.g. affirming the consequent).
In other words, in practice, "non sequitur" refers to an unnamed formal fallacy. Begging the question. Straw man. Post hoc ergo propter hoc. Post hoc ergo propter hoc (Latin: "after this, therefore because of this") is a logical fallacy (of the questionable cause variety) that states "Since event Y followed event X, event Y must have been caused by event X. " Red herring. A red herring is something that misleads or distracts from a relevant or important question.[1] It may be either a logical fallacy or a literary device that leads readers or audiences toward a false conclusion.
A red herring may be used intentionally, as in mystery fiction or as part of rhetorical strategies (e.g., in politics), or may be used in argumentation inadvertently. Irrelevant conclusion. Irrelevant conclusion should not be confused with formal fallacy, an argument whose conclusion does not follow from its premises. Argumentum ad populum. Aristotle, Hegel, and argumentum ad hominem: Rhetoric Society Quarterly: Vol 15, No 3-4. The Greek Roots of the Ad Hominem-Argument. Soundness. Relevance. Formal fallacy. Descriptive statistics. Data modeling. Data mining. Data analysis. Statistical inference.
Jumping to conclusions. Faulty generalization. Deductive reasoning. Irrelevant conclusion. Genetic fallacy. Ad hominem. Reductio ad Absurdum. Reductio ad absurdum. A dialogical interpretation - New APPS: Art, Politics, Philosophy, Science. Definition and Examples of Syllogisms. Aristotelian Syllogisms. Aristotle: Logic. Aristotle's Logic. Definition of Syllogism by Merriam-Webster. Syllogism. Predicable. Predicable. Predicable. Definition of Predicable by Merriam-Webster.