

SolveMe Mobiles. Five Triangles: 251. Some ones. Algebra Tiles- from counting to completing the square. I have become increasingly interested in visual models recently as a way of introducing topics.
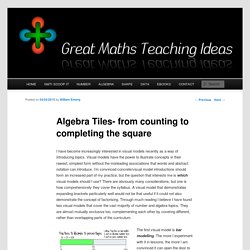
Visual models have the power to illustrate concepts in their rawest, simplest form without the misleading associations that words and abstract notation can introduce. I’m convinced concrete/visual model introductions should form an increased part of my practice, but the question that interests me is which visual models should I use? There are obviously many considerations, but one is how comprehensively they cover the syllabus. A visual model that demonstrates expanding brackets particularly well would not be that useful if it could not also demonstrate the concept of factorising. Through much reading I believe I have found two visual models that cover the vast majority of number and algebra topics. The first visual model is bar modelling. Before I go any further I want to make it clear that I do not think all students need to experience visual models when topics are introduced.
Substitution. Algebraic Product Puzzles. Algebra Tiles. Resourceaholic: Introducing Algebra. Building a solid conceptual understanding of algebra is absolutely fundamental.
As with fractions, it's essential that we get it right because it underpins so much of what follows. But, as with fractions, pupils can really struggle here. Sometimes good teaching resources inspire us when we're looking for ways to structure and deliver our teaching. This post contains some recommendations that may give you food for thought when you’re planning your lessons. MisconceptionsBefore teaching any topic for the first time it's really important to think about potential misconceptions. This activity provided a good opportunity to have individual discussions with pupils and help them make sense of it all. Trial and Improvement. FMSP Algebra Problems. FMSP Quadratics and Cubics Problems. Exponetial Function Card Sort. Dy/dan » Blog Archive » If Graphing Linear Inequalities Are Aspirin, Then How Do You Create The Headache?
This Week’s Skill Here is the first paragraph of McGraw-Hill’s Algebra 1 explanation of graphing linear inequalities: The graph of a linear inequality is the set of points that represent all of the possible solutions of that inequality.
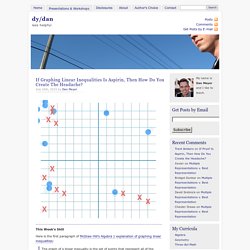
An equation defines a boundary, which divides the coordinate plane into two half-planes. This is mathematically correct, sure, but how many novices have you taught who would sit down and attempt to parse that expert language? Difference of two squares- visual representation. Parallel Lines. Exponent+picture.png (PNG Image, 481 × 257 pixels) Reason and Wonder. As is often the case when a school year winds down, a few ideas have crept into my head that I wish I’d have thought of eight months earlier.
Things are winding down quickly at my school (seniors are done with classes; junior high wraps up this Friday; and high school next Friday), so I’ll share this here in case it’s of use to anyone whose year stretches into June—or for anyone interested in giving this a run in the fall. Step 1. Resourceaholic: New GCSE: Sequences. I've been busy getting my head around the additional sequences content in the new 9 - 1 Maths GCSE and thought it would be helpful to share my findings.

Quite a lot has been added to the higher tier. Previously students covered all the GCSE sequences content at Key Stage 3 so there was nothing new to teach at Key Stage 4. But now we need to include a few weeks' worth of sequences lessons in our GCSE schemes of work. We've gone from this (from the current Pearson Edexcel Specification - GCSE 2012 Maths A): Functions puzzle.png (598×334) Inequalities.png (600×248) Mathematics, Learning and Technology. A previous post on Functions features resources aimed at older students; I thought it would be useful to look at resources for teaching younger students.
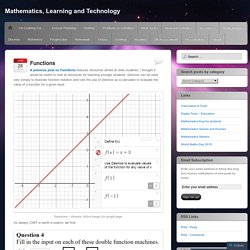
Desmos can be used very simply to illustrate function notation and note the use of Desmos as a calculator to evaluate the value of a function for a given input. Functions – Desmos. Select image for graph page As always CIMT is worth a search; we find: CIMT Interactive Materials – Functions In the interactive materials for year 7: Unit 16 Section 2: Function Machines and there is also a section on the associated text (16.2). TES Resources – Functions On TES, this Crossnumber from cbarthur is an ideal resource for becoming familiar with function notation. AQA Bridging the Gap. Dy/dan » Blog Archive » If Factoring Trinomials is Aspirin Then How Do You Create The Headache? This Week’s Skill Factoring quadratic trinomials. eg.
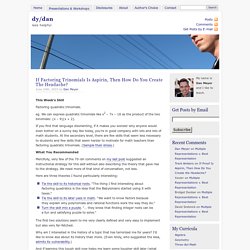
We can express quadratic trinomials like x2 – 7x – 18 as the product of the two binomials: (x – 9)(x + 2). If you find that language disorienting, if it makes you wonder why anyone would even bother on a sunny day like today, you’re in good company with lots and lots of math students. At the secondary level, there are few skills that seem less necessary to students and few skills that seem harder to motivate for math teachers than factoring quadratic trinomials.
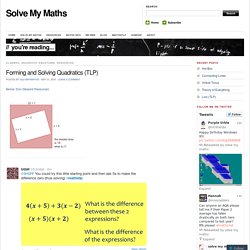
Forming and Solving Quadratics (TLP) Below: Don Steward Resources Forming Quadratics (Shell) About these ads Like this: Like Loading...
Ditch Diggers. Prologue act one 1.
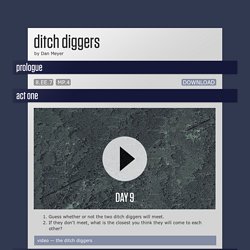
Guess whether or not the two ditch diggers will meet. 2. If they don't meet, what is the closest you think they will come to each other? Video — the ditch diggers. Factorising Quadratic Equations: In Steps. MathArguments180.com: 415: Parallels and Variables. Linear Programming - Lego, Stickers and a bit of sorcery. This is all @fawnpnguyen and @bobloch’s fault.
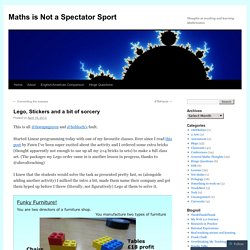
Started Linear programming today with one of my favourite classes. Ever since I read this post by Fawn I’ve been super excited about the activity and I ordered some extra bricks (thought apparently not enough to use up all my 2×4 bricks in sets) to make a full class set. (The packages my Lego order came in is another lesson in progress, thanks to @absvalteaching) I knew that the students would solve the task as presented pretty fast, so (alongside adding another activity) I milked the intro a bit, made them name their company and got them hyped up before I threw (literally, not figuratively) Lego at them to solve it.
I played the awkward teacher game where I refuse to accept any answer they gave me without tons of explanation or evidence. We took a journey through time and space to some years later in the life of their furniture store (now a chain) and presented them with an updated problem that they couldn’t solve through trial and error. Straight line arithmagons.png (640×342) Gradient.png (598×254) Simplifying Radicals: Tug of War - Evaluating Expressions Game. @mathhombre pointed me in the direction of this interesting Tug of War game. Click here. I was playing around with the idea to make it more mathy, and here is what I came up with.
I thought trading cards would be fun and each card looks something like this: Each card would have a function in the top left corner. The game could start with linear functions, and then mix in cards with other functions. In the top right is the suit. Following on from my last post on ideas for the first Year 7 lesson of the year, here's some ideas for the start of Year 12. Unfortunately we don't really have any time to spare in our sixth form teaching. It's a challenge just to fit enough lessons into the school year to cover all the course material before our students go off to take their exams. So, sadly, there's no time for enrichment or getting to know each other - students have to hit the ground running. Entry Assessment At my school, as at many others, we ask our students to prepare for Year 12 by doing some summer work. We expect them to have a solid understanding of GCSE topics when they start the course, particularly surds, indices and algebra.
The results from our entry assessments were rather worrying. I had a huge amount of students come to my extra support sessions - I believe the entry assessment was a good 'wake up call' for them. MEDIAN Don Steward secondary maths teaching: rearrangement steps. Rearrangement steps, with props (or is it 'scaffolding') thanks to Laura Luke and Gareth Hughes for their (mathshub) help. MEDIAN Don Steward secondary maths teaching: cupcakes. Good (except that I'm not a huge fan of cupcakes) context for nth terms and equation solving from the 2015 sample KS2 sample assessments (P2 reasoning Q8) Maths ROTW 83 - Quadratics - Mathematics teaching - TES Mathematics - TES Community. What is it? This is a truly wonderful use of Excel. In fact, possibly the best I have ever seen. Solve My Maths. Sumfrac. AQA 90 problems to solve- perfect for 9-1 Maths GCSE.
AQA have recently released their ’90 problems’ to support teachers in delivering the problem-solving element of the new 9-1 maths GCSE. It’s a rebranding of the 90 problems they released to support the teaching of Further Maths GCSE in 2008. There a number of issues with many of the diagrams on the newer version, so I’ve attached the 2008 version for your interest, here: AQA 90 Problem solving questions. Answers They are excellent resources and perfect for some little-and-often problem solving practice. Highly recommended. MEDIAN Don Steward secondary maths teaching: simple linear relationships. A simpler version of linear relationships. MEDIAN Don Steward secondary maths teaching: quadratic matchstick patterns. MEDIAN Don Steward secondary maths teaching: V-problems.
It may be helpful for students to put the expressions on bits of paper - to be able to change the arrangement more easily. MEDIAN Don Steward secondary maths teaching: six legs. Simpler versions of transformational spiders thanks to Aimee and Dan (Telford and Wrekin primary school teachers), working on a Mathshub primary algebra project. Lesson Collection 81: Function Machines - TES ROTW 81 - Mr Barton Maths Blog. For the next few weeks, the ROTW will be looking at examples of complete lessons on TES. I find resources like this fascinating, as they give you a real insight into a teacher’s thinking, far more than you would get from a PowerPoint or a worksheet alone. The advice I give to all trainee teachers and NQTs that I work with is to take lessons like this, study them, and then adapt them to suit their own teaching style and the needs of their students.
As ever, I am eternally indebted to teachers for sharing their resources on TES, but a special thank you to those who upload complete lessons like this. Regions- stained glass windows. A lovely idea from a colleague- regions stained glass windows… MEDIAN Don Steward secondary maths teaching: geometric series, some with surds. MEDIAN Don Steward secondary maths teaching: angles with algebra. MEDIAN Don Steward secondary maths teaching: rearrangement add/take. Thanks to Dave Hewitt for his thoughts on the 'shape' of what rearrangement looks like.
MEDIAN Don Steward secondary maths teaching: rules to points. MEDIAN Don Steward secondary maths teaching: rearrangement times/divide. MEDIAN Don Steward secondary maths teaching: formulas. Some formulas from past KS3 SAT papers. Simplifying Radicals: Updated Version of Tornado Inequality Game. A long time ago, I created a game for systems of linear inequalities. Click here to read about it. Simplifying Radicals: Operations with Monomials Game - Version 2. If you are just tuning in and missed Version 1, click here to read about that version. I am creating different versions of games that reinforce operations with monomials. Here is version 2. Who, What, When, Where, Why? MEDIAN Don Steward secondary maths teaching: ducks nth term. MEDIAN Don Steward secondary maths teaching: so... Algebra: Changing the Subject (TLP) Simultaneous scenarios - Algebra - Simultaneous equations - Algebra - Key Stage 4 - Resources. Simplifying Radicals: Writing Linear Equations Given Two Ordered Pairs. MEDIAN Don Steward secondary maths teaching: equation forming and solving.
GCSE New Content – Iterative Methods for Numerical Solution of Equations. Simultaneous Equations. Simultaneous Equations (TLP) Resourceaholic: New GCSE: Inequalities. Inequalities and Linear Programming. MEDIAN Don Steward secondary maths teaching: self-inverse and periodic functions. Functions. FMSP Function Problems. New secondary mathematics curriculum: Sequences - Mathematics teaching - TES Mathematics - TES Community. Jumping along a line. MEDIAN Don Steward secondary maths teaching: nth term as a strip. Visual Patterns. Geometric Sequence Sort Cards. Finding the nth Term (TLP) Geometric Sequences Worksheet. Quadratic Equations and Complex Numbers. Categorising Quadratic Curves. Equations of Lines (TLP) Perpendicular Lines. Axis. Parabola - Interactive Graphs. Plotting Curves and Parametric Equations.
Straight Line Graphs Sketch For Presents Game - Resources - TES. Water Line by Desmos. Linear Relationships. Expanding Brackets (TLP) Loop cards. Resourceaholic: Tricks and Tips 2: Sequences, Linear Graphs and Surds. Consecutive Sums. Grid Relationsips. 3D printing and the quadratic curve. MEDIAN Don Steward secondary maths teaching: fifteen pens. Binomial Expansion. MEDIAN Don Steward secondary maths teaching: rectangle dissection. MEDIAN Don Steward secondary maths teaching: starfish. Tools For Manipulating Equations (TLP) MEDIAN Don Steward secondary maths teaching: equations with tables practice. Forming Equations (TLP) Solving inequalities and equations (TLP)
MEDIAN Don Steward secondary maths teaching: nth term halving. MEDIAN Don Steward secondary maths teaching: squares nth term. MEDIAN Don Steward secondary maths teaching: one incorrect simplification. MEDIAN Don Steward secondary maths teaching: grid moves. MEDIAN Don Steward secondary maths teaching: the stories of 6. MEDIAN Don Steward secondary maths teaching: expressions arithmagons.