

SCIENCE. Scientific Representation. Symbolica. LogicKo. List of mathematical symbols. When reading the list, it is important to recognize that a mathematical concept is independent of the symbol chosen to represent it.
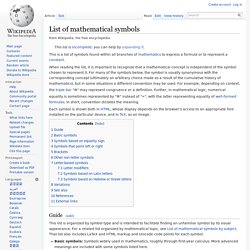
For many of the symbols below, the symbol is usually synonymous with the corresponding concept (ultimately an arbitrary choice made as a result of the cumulative history of mathematics), but in some situations a different convention may be used. For example, depending on context, the triple bar "≡" may represent congruence or a definition. Further, in mathematical logic, numerical equality is sometimes represented by "≡" instead of "=", with the latter representing equality of well-formed formulas.
In short, convention dictates the meaning. Each symbol is shown both in HTML, whose display depends on the browser's access to an appropriate font installed on the particular device, and in TeX, as an image. Guide[edit] This list is organized by symbol type and is intended to facilitate finding an unfamiliar symbol by its visual appearance. Basic symbols[edit] Free Online Math Calculator and Converter. Simplifying with Nested Parentheses. Simplifying with Nested Parentheses (page 2 of 3)
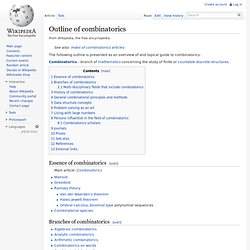
Fractale. Mandelbrot Set. Patterns of Math - Visual Guide to the Mandelbrot Set. The Encyclopedia of the Mandelbrot Set at MROB. A second-order embedded Julia set This is a picture from the Mandelbrot Set, one of the most well-known fractal images in the world.

(Click it for a larger version). The Mandelbrot Set is one of my hobbies, and I have collected a large amount of information about it. To organize that information I have created Mu-Ency, a large collection of text files linked to each other. Torus. Algorithms. Equations - EquationSheet.com. Calculating the Distance to the Horizon.
For Any Game Home Up Site Map Assumptions | Method 1 | Method 2 Method 1 | Method 2 This is all based on the assumption that the horizon is the point on the world's surface at which the line of sight of the viewer, whatever their height, becomes parallel (tangential) to the surface of the world, and meets the surface of the world (so that the viewer cannot see any further than it).
It also assumes a perfectly spherical world, and does not take into account any effects on the visible horizon due to terrain or atmospheric refraction. Note that I do not mention units in any of the equations on this page. Assumptions | Method 2. Pythagoras Proof of the Existence of Irrational Numbers.
RANDOM.ORG - True Random Number Service. Probability theory. Outline of combinatorics. The following outline is presented as an overview of and topical guide to combinatorics: Combinatorics – branch of mathematics concerning the study of finite or countable discrete structures.
Essence of combinatorics[edit] Main article: Combinatorics Branches of combinatorics[edit] Multi-disciplinary fields that include combinatorics[edit] The Electronic Journal of Combinatorics. Probability and Statistics. Mathematics. Math. Astronomical Paradigms. MATLAB - Le langage du calcul scientifique - MathWorks France. MATLAB® is a high-level language and interactive environment for numerical computation, visualization, and programming.

Using MATLAB, you can analyze data, develop algorithms, and create models and applications. The language, tools, and built-in math functions enable you to explore multiple approaches and reach a solution faster than with spreadsheets or traditional programming languages, such as C/C++ or Java™. You can use MATLAB for a range of applications, including signal processing and communications, image and video processing, control systems, test and measurement, computational finance, and computational biology. More than a million engineers and scientists in industry and academia use MATLAB, the language of technical computing. Purplemath. Friendly lessons for lasting insight. Factoids > big numbers. Numbers go on for ever, but our notation does not. If you want to write down the value of a very big number (way bigger even than a googolplex ), the mathematical notations for factorial or exponentiation, the fastest growing 'conventional' functions, eventually becomes unweildy; you get too many factorials or exponents to manipulate easily.
Something more extensible is needed. The so-called "large primes " -- useful for cryptography -- are relatively small compared to the kind of numbers that soon arise in these notations. Knuth's up-arrow notation In 1976 Donald Knuth published his up-arrow notation for large numbers. M n = m + m + ... + m ( n terms) = m × n. Factoids > googol / googolplex. Words of wisdom are spoken by children at least as often as by scientists.

The name 'googol' was invented by a child (Dr Kasner's nine-year-old nephew) who was asked to think up a name for a very big number, namely, 1 with a hundred zeros after it. He was very certain that this number was not infinite, and therefore equally certain that it had to have a name. At the same time that he suggested 'googol' he gave a name for a still larger number: 'Googolplex'. Discrete Math Lecture Notes. Erdös Number Project - The Erdös Number Project. Göttinger Digitalisierungszentrum: Seitenansicht. Research > Non-Standard Computation. C-ship: Relativistic ray traced images. C-ship: Relativistic ray traced images Welcome aboard C-ship, exploring flight near the speed of light!

C-ship helps you understand Einstein's theory of Special Relativity intuitively through the medium of computer-synthesised images. To view the images in this document, you need a graphics-oriented Web browser. We'll be looking at lots of pictures on our journey. Sending large pictures across the Internet consumes precious network bandwidth and can take a long time. Our Sturdy Craft. Engineering ToolBox. Wolfram MathWorld: The Web's Most Extensive Mathematics Resource.
Alpha: Computational Knowledge Engine. If people do not believe that mathematics is simple, it is only. If people do not believe that mathematics is simple, it is only because they do not realize how complicated life is Scanning Electron Micrographs of Diatoms Title: John von Neumann.
The Story of Mathematics - Sumerian/Babylonian Mathematics. Sumer (a region of Mesopotamia, modern-day Iraq) was the birthplace of writing, the wheel, agriculture, the arch, the plow, irrigation and many other innovations, and is often referred to as the Cradle of Civilization.

The Sumerians developed the earliest known writing system - a pictographic writing system known as cuneiform script, using wedge-shaped characters inscribed on baked clay tablets - and this has meant that we actually have more knowledge of ancient Sumerian and Babylonian mathematics than of early Egyptian mathematics. Indeed, we even have what appear to school exercises in arithmetic and geometric problems. As in Egypt, Sumerian mathematics initially developed largely as a response to bureaucratic needs when their civilization settled and developed agriculture (possibly as early as the 6th millennium BCE) for the measurement of plots of land, the taxation of individuals, etc.
In the Babylonian system represented 3,600 plus 60 plus 1, or 3,661. The Historical Development of Mathematics. By Rit Nosotro Change Over Time essay Describe the development of mathematics.

Thesis: Summary: With our modern understanding of mathematics, its historical development may seem straightforward, and the ideas we have inherited about mathematics appear obvious. What seems most obvious to us is that ten numerals are used in various combinations to express all possible real numbers; this is a base ten system with place values. Isopsephy. Isopsephy (/ˈaɪsəpˌsɛfi/; ἴσος isos meaning "equal" and ψῆφος psephos meaning "pebble") is the Greek word for the practice of adding up the number values of the letters in a word to form a single number. The early Greeks used pebbles arranged in patterns to learn arithmetic and geometry. Isopsephy is related to Gematria, the same practice using the Hebrew alphabet, and the ancient number systems of many other peoples (for the Arabic alphabet version, see Abjad numerals).
A Gematria of Latin-script languages was also popular in Europe from the Middle Ages to the Renaissance and indeed its legacy remains in numerology and Masonic symbolism today (see arithmancy).[1] History[edit] Until Arabic numerals were adopted and adapted from Indian numerals in the 8th and 9th century AD, and promoted in Europe by Fibonacci of Pisa with his 1202 book Liber Abaci, numerals were predominantly alphabetical. "Nero, Orestes, Alcmeon their mothers slew. A calculation new. Καισαρ, Νειλαιη Μουσα Λεωνιδεω. Book sources.
This page allows users to search for multiple sources for a book given the 10- or 13-digit ISBN number. Spaces and dashes in the ISBN number do not matter. In Wikipedia, numbers preceded by "ISBN" link directly to this page. This page links to catalogs of libraries, booksellers, and other book sources where you will be able to search for the book with ISBN. If you arrived at this page by clicking an ISBN number link in a Wikipedia page, then the links below (those labeled "find this book") search for the specific book using that ISBN number. Network Science. TECHNOLOGY. Complex Systems. Newer Technology. New Engineers.