

The Subtle Art of the Mathematical Conjecture. Mountain climbing is a beloved metaphor for mathematical research. The comparison is almost inevitable: The frozen world, the cold thin air and the implacable harshness of mountaineering reflect the unforgiving landscape of numbers, formulas and theorems. And just as a climber pits his abilities against an unyielding object — in his case, a sheer wall of stone — a mathematician often finds herself engaged in an individual battle of the human mind against rigid logic. In mathematics, the role of these highest peaks is played by the great conjectures — sharply formulated statements that are most likely true but for which no conclusive proof has yet been found. These conjectures have deep roots and wide ramifications. Quanta Magazine. We like to say that anything is possible.
In Norton Juster’s novel The Phantom Tollbooth, the king refuses to tell Milo that his quest is impossible because “so many things are possible just as long as you don’t know they’re impossible.” In reality, however, some things are impossible, and we can use mathematics to prove it. People use the term “impossible” in a variety of ways.
It can describe things that are merely improbable, like finding identical decks of shuffled cards. It can describe tasks that are practically impossible due to a lack of time, space or resources, such as copying all the books in the Library of Congress in longhand. Quanta Magazine. After coming up with this architecture, the researchers used a bank of elementary functions to generate several training data sets totaling about 200 million (tree-shaped) equations and solutions.
They then “fed” that data to the neural network, so it could learn what solutions to these problems look like. After the training, it was time to see what the net could do. The computer scientists gave it a test set of 5,000 equations, this time without the answers. (None of these test problems were classified as “unsolvable.”) The neural net passed with flying colors: It managed to get the right solutions — precision and all — to the vast majority of problems. For almost all the problems, the program took less than 1 second to generate correct solutions.
Despite the results, the mathematician Roger Germundsson, who heads research and development at Wolfram, which makes Mathematica, took issue with the direct comparison. A quantum technique highlights math’s mysterious link to physics. It has long been a mystery why pure math can reveal so much about the nature of the physical world.
Antimatter was discovered in Paul Dirac’s equations before being detected in cosmic rays. Quarks appeared in symbols sketched out on a napkin by Murray Gell-Mann several years before they were confirmed experimentally. Einstein’s equations for gravity suggested the universe was expanding a decade before Edwin Hubble provided the proof.
Einstein’s math also predicted gravitational waves a full century before behemoth apparatuses detected those waves (which were produced by collisions of black holes — also first inferred from Einstein’s math). Nobel laureate physicist Eugene Wigner alluded to math’s mysterious power as the “unreasonable effectiveness of mathematics in the natural sciences.” But maybe there’s a new clue to what that explanation might be. Sign Up For the Latest from Science News Headlines and summaries of the latest Science News articles, delivered to your inbox. A quantum technique highlights math’s mysterious link to physics. Without a Proof, Mathematicians Wonder How Much Evidence Is Enough.
Great Literature Is Surprisingly Arithmetic. A good book evokes a variety of emotions as you read.
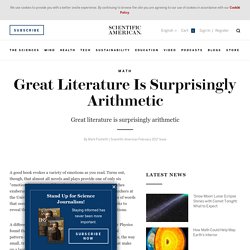
Turns out, though, that almost all novels and plays provide one of only six “emotional experiences” from beginning to end—a rags-to-riches exuberance, say, or a rise and fall of hope (below, top). Researchers at the University of Vermont graphed the happiness and sadness of words that occurred across the pages of more than 1,300 fiction works to reveal the emotional arcs and discovered relatively few variations. A different study coordinated by Poland's Institute of Nuclear Physics found that sentence lengths in books frequently form a fractal pattern—a set of objects that repeat on a small and large scale, the way small, triangular leaflets make up larger, triangular leaves that make up a larger, triangular palm frond (below, bottom). Why analyze the mathematics of literature? Vermont applied mathematician Andrew J. MathSite: An Interactive Source for Seeing, Hearing, Doing Mathematics.
Famed number π found hidden in the hydrogen atom. Three hundred and sixty years ago, British mathematician John Wallis ground out an unusual formula for π, the famed number that never ends.
12 Mind Blowing Number Systems From Other Languages. Today is a big day for lovers of the number 12, and no one loves 12s more than the members of the Dozenal Society.
The Dozenal Society advocates for ditching the base-10 system we use for counting in favor of a base-12 system. Because 12 is cleanly divisible by more factors than 10 is (1, 2, 3, 4, 6 and 12 vs. 1, 2, 5 and 10), such a system would neaten up our mathematical lives in various ways. But a dozenal system would require us to change our number words so that, for example, what we know as 20 would mean 24 (2x12), 30 would mean 36, and so on. How To Slice A Bagel Along A Mobius Strip — And Why. In the weeks before Doug Sohn closed down his legendary Chicago sausage joint Hot Doug’s, people were literally walking in the door and offering him a million dollars to stay open.
Doing the Math (Updated)
Scale2/scale2.swf?bordercolor=white. Many Variables in a New York Math Museum. Vi Hart: Math Doodling. Remember that video about doodling dragons and fractals and stuff?
I finally finished part 2! Here is a magnet link so you can dowload it via torrent. Steven Strogatz on the Elements of Math - Series.