

Conditional Probability & Bayes' Theorem - Calvin Lin. By Matt Enlow Probability problems are notorious for yielding surprising and counterintuitive results.

One famous example -- or pair of examples -- is the following: 1. A couple has two children and the older child is a boy. If the probabilities of having a boy or a girl are both , what is the probability that the couple has two boys? There are several approaches we could take to straighten out this logical tangle, as well as many other tangles that arise in probability. When calculating probabilities of certain events, we often obtain new information that may cause our calculations to change.
Let’s define the events and as “the card is a Heart”and “the card is red,” respectively. What about the values of and ? Bayes’ Theorem For any two events and , The proof of Bayes' Theorem follows from the fact that both and are equivalent to , the probability of both events occurring. Help me understand Bayesian prior and posterior distributions. Search lectures Bayesian. Search: Bayesian Events Bayesian Research Kitchen Workshop (BARK), Grasmere 2008 **Motivation**\\ The main aim of this workshop is to allow leading Bayesian researchers in machine **\\ * Incorporating Complex Prior Knowledge in Bayesian inference, for example mechanistic models (such as Processes). * Model mismatch: the Bayesian lynch pin is that the model is correct, but it rarely is . * Approximation techniques: how should we do Bayesian inference in practice.
Sampling, variational, Laplace or something else? * Your pet Bayesian issue here. Understanding Bayes' Theorem. Machine Learning Summer School 2013. Alexander Kruel · A Guide to Bayes’ Theorem – A few links. Prototype ML/NLP Code Tutorial Series Lesson 3: Bayes Theorem. Welcome to the third lesson in our Machine Learning/Natural Language Processing Tutorial Series.
Last time we discussed some of the concepts from probability you’ll need in ML/NLP. If you haven’t read the previous lesson we encourage you to do so before proceeding. This lesson directly builds on concepts discussed in the previous. In this lesson we are going to look at more advanced probability related questions and procedures. In the previous lesson we discussed the most simple case – probabilities of independent variables. We have arrived at the point where we can discuss Bayes Theorem, the key component to our first ML algorithm – the Naive Bayes Classifier. The code for this lesson is available on github.
Mutually Exclusive vs Inclusive Probabilities An important concept in probability and statistics is that of exclusive vs inclusive probabilities. Understand Bayes Theorem (prior/likelihood/posterior/evidence) Bayes Theorem is a very common and fundamental theorem used in Data mining and Machine learning.
Its formula is pretty simple: P(X|Y) = ( P(Y|X) * P(X) ) / P(Y), which is Posterior = ( Likelihood * Prior ) / Evidence So I was wondering why they are called correspondingly like that. Let’s use an example to find out their meanings. Suppose we have 100 movies and 50 books. An Intuitive (and Short) Explanation of Bayes’ Theorem. Bayes’ theorem was the subject of a detailed article.

The essay is good, but over 15,000 words long — here’s the condensed version for Bayesian newcomers like myself: Tests are not the event. We have a cancer test, separate from the event of actually having cancer. We have a test for spam, separate from the event of actually having a spam message.Tests are flawed. Tests detect things that don’t exist (false positive), and miss things that do exist (false negative).Tests give us test probabilities, not the real probabilities. Probably Overthinking It: My favorite Bayes's Theorem problems. This week: some of my favorite problems involving Bayes's Theorem.
Next week: solutions. 1) The first one is a warm-up problem. I got it from Wikipedia (but it's no longer there): Suppose there are two full bowls of cookies. Bowl #1 has 10 chocolate chip and 30 plain cookies, while bowl #2 has 20 of each. Set symbols of set theory (Ø,U,{},∈,...)
Probabilistic Models of Cognition. Artificial Intelligence - foundations of computational agents. Whoso neglects learning in his youth, loses the past and is dead for the future. - Euripides (484 BC - 406 BC), Phrixus, Frag. 927 Learning is the ability of an agent to improve its behavior based on experience.

This could mean the following: The range of behaviors is expanded; the agent can do more. The accuracy on tasks is improved; the agent can do things better. The ability to learn is essential to any intelligent agent. Chapter 11 goes beyond supervised learning and considers clustering (often called unsupervised learning), learning probabilistic models, and reinforcement learning. Streeter-2009-A-Hierarchical-Empirical-Bayesian-Model-poster.png (PNG Image, 3600 × 2400 pixels) - Scaled (28%) Bayesian Inference. Tenenbaum: How to grow a mind: Statistics, structure,... How to Grow a Mind: Statistics, Structure and Abstraction. Bayesian Methods for Hackers.
An intro to Bayesian methods and probabilistic programming from a computation/understanding-first, mathematics-second point of view.

Prologue The Bayesian method is the natural approach to inference, yet it is hidden from readers behind chapters of slow, mathematical analysis. The typical text on Bayesian inference involves two to three chapters on probability theory, then enters what Bayesian inference is. Unfortunately, due to mathematical intractability of most Bayesian models, the reader is only shown simple, artificial examples. Nonparametric Bayes Tutorial. A very good reference on abstract Bayesian methods, exchangeability, sufficiency, and parametric models (including infinite-dimensional Bayesian models) are the first two chapters of Schervish's Theory of Statistics.
[MathSciNet] Posterior convergence A clear and readable introduction to the questions studied in this area, and to how they are addressed, is a survey chapter by Ghosal which is referenced above. The following monograph is a good reference that provides many more details. Be aware though that the most interesting work in this area has arguably been done in the past decade, and hence is not covered by the book. Exchangeability. Bayesian. Bayesian refers to any method of analysis that relies on Bayes' equation.
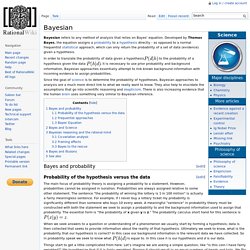
Developed by Thomas Bayes, the equation assigns a probability to a hypothesis directly - as opposed to a normal frequentist statistical approach, which can only return the probability of a set of data (evidence) given a hypothesis. In order to translate the probability of data given a hypothesis to the probability of a hypothesis given the data , it is necessary to use prior probability and background information. TomGriffiths_slides.pdf. Selected publications. In-depth introduction to machine learning in 15 hours of expert videos. In January 2014, Stanford University professors Trevor Hastie and Rob Tibshirani (authors of the legendary Elements of Statistical Learning textbook) taught an online course based on their newest textbook, An Introduction to Statistical Learning with Applications in R (ISLR). I found it to be an excellent course in statistical learning (also known as “machine learning”), largely due to the high quality of both the textbook and the video lectures.
And as an R user, it was extremely helpful that they included R code to demonstrate most of the techniques described in the book. If you are new to machine learning (and even if you are not an R user), I highly recommend reading ISLR from cover-to-cover to gain both a theoretical and practical understanding of many important methods for regression and classification. It is available as a free PDF download from the authors’ website. The BayesiaLab Library - Home - BayesiaLab's Library. Cocosci.berkeley.edu/tom/papers/bayeschapter.pdf. Artificial Neural Networks Technology - TOC. The Nature of Code. “You can’t process me with a normal brain.” — Charlie Sheen We’re at the end of our story. This is the last official chapter of this book (though I envision additional supplemental material for the website and perhaps new chapters in the future). We began with inanimate objects living in a world of forces and gave those objects desires, autonomy, and the ability to take action according to a system of rules.
Next, we allowed those objects to live in a population and evolve over time.