

Une hypothèse sur l'origine quantique virtuelle de la gravitation entre particules de masse inerte. Une hypothèse sur l’origine quantique virtuelle de la gravitation entre particules de masse inerte Un lecteur me demande quelle est, selon moi, la nature et l’origine de la gravitation entre deux masses.
On se souvient que, si cette gravitation est la première des forces à avoir été découverte et mise en équation, elle n’a toujours pas donné la clef de son origine. La masse volumique. Trigonometrie. Science et recherche. Nombres. Introduction à la logique mathématique. Nous avons maintenant tous les outils en main pour réaliser des raisonnements mathématiques complets.
Un raisonnement permet d'établir une proposition à partir d'une ou de plusieurs propositions initiales admises (ou précédemment démontrées) en suivant les règles de la logique. Nous allons dans cette dernière partie détailler quatre "types" de raisonnement, quatre "méthodes" pour démontrer une proposition : Trouver un exemple ou un contre-exempleDémontrer la contraposéeRaisonner par l'absurdeRaisonner par récurrence Ces différentes formes de raisonnements devront s'appliquer dans des cas bien particuliers. Exemple et contre exemple. Tableurs. Le nombre d'or et la composition d'un tableau.
Le temps et les sciences. Art & mathématique. MOOC Cryptographie. Comment crypte-t-on les données sur Internet ? - Kezako ? Introduction aux différents ensembles de nombres. Nombres Clés. Nombre d'or. Nombre d'or, divine proportion,section dorée. ##Composition et règle des 1/3. Si vos photos manquent d’impact, vérifiez si vous avez suivi la règle des tiers.
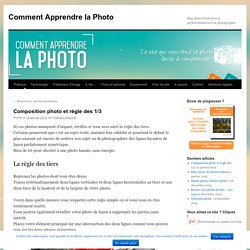
Certains penseront que c’est un sujet éculé, maintes fois rabâché et pourtant le défaut le plus courant est encore de centrer son sujet ou de photographier des lignes fuyantes de façon parfaitement symétrique. Rien de tel pour aboutir à une photo banale, sans énergie. La règle des tiers Reprenez les photos dont vous êtes déçus. Tracez systématiquement deux lignes verticales et deux lignes horizontales au tiers et aux deux tiers de la hauteur et de la largeur de votre photo. Voyez dans quelle mesure vous respectez cette règle simple ou si vous vous en êtes totalement écarté. Cette recette de composition fonctionne bien ! Cette photo est bien composée et gagnerait encore en impact avec un fond plus flou. Composition et photographie.
Mathématiques. Injection (mathématiques) Un article de Wikipédia, l'encyclopédie libre.
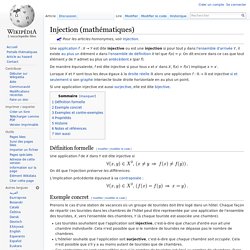
De manière équivalente, f est dite injective si pour tous x et x′ dans X, f(x) = f(x′) implique x = x′. Lorsque X et Y sont tous les deux égaux à la droite réelle ℝ alors une application f : ℝ → ℝ est injective si et seulement si son graphe intersecte toute droite horizontale en au plus un point. Une chambre hyperbolique. Peut-on imaginer une géométrie où tous les axiomes seraient satisfaits, sauf le cinquième ?
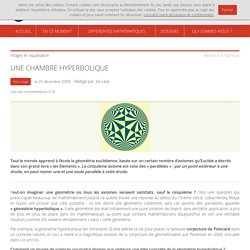
C’est une question qui préoccupait beaucoup de mathématiciens jusqu’à ce qu’elle trouve une réponse au début du 19-ème siècle. Lobachevsky, Bolyai et Gauss ont prouvé que c’est possible : ils ont décrit une géométrie cohérente sans cet axiome des parallèles, appelée « géométrie hyperbolique ». ASTOUNDING: 1 + 2 + 3 + 4 + 5 + ... = -1/12. Géométrie hyperbolique. En mathématiques, la géométrie hyperbolique (nommée parfois géométrie de Lobatchevski) est une géométrie non euclidienne vérifiant les quatre premiers postulats de la géométrie euclidienne, mais pour laquelle le postulat euclidien des parallèles est remplacé par le postulat que « par un point extérieur à une droite passe plus d'une droite parallèle ».
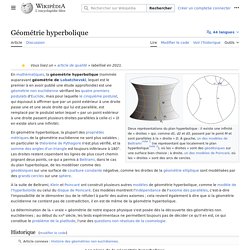
On démontre qu'alors il y a une infinité de droites parallèles. En géométrie hyperbolique, le théorème de Pythagore n'est plus valable et la somme des angles d'un triangle n'est plus égale à 180°. Une droite est toujours définie comme la ligne de plus court chemin joignant deux points sur une surface. Lobatchevski[1], Klein et Poincaré ont créé des modèles de géométrie non euclidienne dans lesquels on peut tracer une infinité de parallèles à une droite donnée et passant par un même point. On peut citer, en deux dimensions : le disque de Poincaré, le demi-plan de Poincaré…
Liste de concepts logiques. Un article de Wikipédia, l'encyclopédie libre.
Cet article liste les principaux concepts logiques, au sens philosophique du terme, c'est-à-dire en logique générale (issue de la dialectique). Nota : Liste des concepts logiques de la philosophie. Logique modale. Un article de Wikipédia, l'encyclopédie libre.
La logique modale est un type de logique qui permet de formaliser des éléments modaux. Exemple d'éléments modaux : « il est possible », « il est nécessaire », etc. Par exemple, on peut utiliser la proposition « Il pleut » comme ceci : Convertisseurs très divers. Panneau circulation alternée - Cours code de la route cours Vidéo. Les Fractions. Logique. Excel. JEUX SERIEUX. Fractions. Première carte corporelle des emotions. TV5 Monde - Jeux d'entraînement cérébral.
Chroniques du début de la fin du pétrole, par Matthieu Auzanneau. 139SD&LDB. « Les enfants à "hautes potentialités" semblent souvent devancer, anticiper les données objectives de la tâche, avec une sorte d'acuité qui leur donne comme intuitivement une solution globale, freinant parfois l'élan de l'action et la réalisation et ceci d'autant plus qu'ils sont sensibles à leur différence, ce qu'ils éprouvent vis-à-vis de l'autre les rendant hostiles à toute prise de risque.
Comportement qui peut, à tort, être interprété comme une immaturité affective (alors que l'on pourrait plutôt parler d'hypermaturité) ou marquer des traits d'un dysfonctionnement psychopathologique (isolement social, difficulté du maintien du regard lors d'une conversation, fuite du regard pouvant apparaître comme une phobie visuelle ou une caractéristique autistique). Ainsi qu'Alain Gauvrit (15) : En conclusion. Qu'est-ce que la vérite mathématique ? Putnam. Qu'est-ce que la vérité mathématique ?

[extrait] traduction provisoire par Hilary PUTNAM Edition originale : What is mathematical truth ? In Putnam H. : Mathematics, Matter and Method. Traduit de l’anglais (USA) par Patrick PeccatteAvertissement : Cette traduction est présentée à titre d'illustration, comme une longue citation. . [...] Théorème de Jordan. Un article de Wikipédia, l'encyclopédie libre. En mathématiques, le théorème de Jordan est un théorème de topologie plane.
Il est célèbre par le caractère apparemment intuitif de son énoncé et la difficulté de sa démonstration. « En fait, il n'y a pratiquement aucun autre théorème qui apparaisse aussi évident en apparence que n'importe quel axiome de géométrie élémentaire et dont la preuve est tout sauf évidente »[1] précise M. Dostal à son sujet. Si, à l'aide d'un crayon, on dessine une ligne continue (on ne lève pas le crayon) qui ne se croise pas et qui termine là où elle commence, la zone de la feuille non dessinée se décompose en deux parties, l'intérieur de la figure, qui est borné, et l'extérieur, qui ne le serait pas si la feuille ne l'était pas. Problème des partis. Un article de Wikipédia, l'encyclopédie libre. Le problème des partis[1] est une question, apparemment très simple[2] et portant sur les jeux de hasard, qui joue un rôle fondamental dans l'histoire de la mathématisation du hasard et l'émergence d'une théorie mathématique du probable et du calcul des probabilités à partir des travaux de Blaise Pascal et de Christian Huygens au milieu du XVIIe siècle.
Espace Analytique A.F.P.R.F. Liste de concepts logiques. Calcul Maths... Robert Blanché -> logical hexagon. The homepage of NOT (N-Opposition Theory): Oppositional Geometry. Pierre Lochak. La Théorie des Cordes. Francis Bacon. Citations[modifier] Le médecin (...), pour guérir la maladie, tue le malade. (en) Cure the disease, and kill the patient.Essais du chevalier Bacon (texte en ligne), chancelier d’Angleterre, sur divers sujets de politique, & de morale, Francis Bacon, éd. Chez Emery, 1734, p. 213. Citation choisie citation du jour pour le 2 octobre 2009. Jacques Bouveresse. Jacques Bouveresse , né le 20 août 1940, est un philosophe français . Il est aujourd'hui professeur au Collège de France où il occupe la chaire de philosophie du langage et de la connaissance , succédant à son maître et ami Jules Vuillemin . Essais II , 2001 [ modifier ] Bertrand Russell. Bertrand Russell, 1916. Bertrand Russell (Tellek, Monmouthshire, 18 mai 1872 - près de Penrhyndeudraeth, Pays de Galles, 2 février 1970 ), était un logicien , philosophe et homme politique britannique.
La méthode scientifique en philosophie|La méthode scientifique en philosophie [ modifier ] La logique pour les nuls : 3. La logique pour les nuls :2 b. La logique pour les nuls :2 a. La logique pour les nuls : 1. Bataille de fractions. Apprendre les tables de multiplication. Calcul - Logique - Applications maths... Poincaré wittgensteinien ? Sans vouloir présenter Poincaré comme une sorte de précurseur de Wittgenstein, l'auteur se propose de montrer que la lecture de Wittgenstein peut, dans certains cas, être une propédeutique utile à la lecture de Poincaré. Philosophie des mathématiques et thérapeutique d’une maladie philosophique: Wittgenstein et la critique de l’apparence ontologique dans les mathématiques. Catalogue Périodiques Nouveautés Home Accueil Bibliothèque Interuniversitaire Liens Utiles. Mathématiques. Théorie générale de la connaissance. M. Schlick. NRF; « bibliothèque de philosophie ». Gallimard (2009). 548 pp. ISBN: 978-2-07-077185-1. (index inclus) (Traduit de l’allemand et présenté par Christian Bonnet)
Catalogue Périodiques Nouveautés Home Accueil Bibliothèque Interuniversitaire Liens Utiles. Gamesserious. Logique-mathématique. Pierre Perroud - Jacques BOUVERESSE, Qu'appellent-ils "penser"? Quelques remarques à propos de l'"affaire Sokal" et de ses suites. Philosophy of probability.
Paradoxe - Jean-Paul Delahaye. Images des mathématiques. 2+2=5 Humor in der Mathematik. Bric-à-Brac.