

Relaciones y funciones. Entender los conceptos de Relación y de Función es de suma importancia en Matemática.
Para lograr esa comprensión es necesario adentrarnos en la noción de Correspondencia, ya que esta tiene un papel fundamental en las relaciones y funciones. Lo primero es entender que Correspondencia es equivalente a Relación. En nuestra lengua, decir “en relación a”, es equivalente a decir “corresponde a”. Ejemplos: En una tienda comercial, cada artículo está relacionado con su precio; o sea, a cada artículo le corresponde un precio. En la guía telefónica, cada cliente está relacionado con un número; o sea, a cada nombre de la guía le corresponde un número. Definición matemática de Relación y de Función En matemática, Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamado Recorrido o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango. Todas las Relaciones pueden ser graficadas en el Plano Cartesiano. Algebra: Capítulo 2: Relaciones y funciones. Khan Academy.
Get The Math. Relaciones y Funciones. Jerarquía de operaciones. Fracciones. Ejercicios. A.2.4.4. Ejercicio operaciones combinadas. Sumar,restar,multiplicar y dividir. Ejercicios para números decimales: sumar, restar, multiplicar y dividir. Imprimir gratis hojas de ejercicios por: MamutMatematicas.com. Este generador de hojas de ejercicios elabora ejercicios de las cuatro operaciones básicas con números decimales (es decir, números con décimos, centésimos, milésimos, etcétera después del punto (de la coma) decimal).
Se pueden realizar ejercicios fáciles de "aritmética mental" o ejercicios de multiplicación por 10 o 100 para escuela primaria. También puedes realizar ejercicios de suma, resta, multiplicación y división en fila (horizontal) o en columna (vertical) para escuela secundaria. Puede escoger el punto o la coma decimal como separador decimal. ¡Prueba las diferentes opciones que te ofrece el generador de ejercicios para personalizar la hoja de ejercicios según tus gustos y necesidades! SUMA , RESTA , MULTIPLICACION Y DIVISION DE NUMEROS DECIMALES. Proporcionalidad: Directa e Inversa. Para comprender el concepto de proporcionalidad, directa o inversa, debemos comenzar por comprender el concepto de razón.
Razón y proporción numérica Razón entre dos números Siempre que hablemos de Razón entre dos números nos estaremos refiriendo al cociente (el resultado de dividirlos) entre ellos. Entonces: Proporción numérica Ahora, cuando se nos presentan dos razones para ser comparadas entre sí, para ver como se comportan entre ellas, estaremos hablando de una proporción numérica. Los números 2, 5 y 8, 20 forman una proporción, ya que la razón entre 2 y 5 es la misma que la razón entre 8 y 20. se cumple que el producto de los extremos nos da 2 x 20 = 40 y el producto de los medios nos da 5 x 8 = 40 Comprendido el concepto de proporción como una relación entre números o magnitudes, ahora veremos que esa relación puede darse en dos sentidos: Las dos magnitudes pueden subir o bajar (aumentar o disminuir) o bien si una de las magnitudes sube la otra bajo y viceversa.
Matemática Multiplicación y división de decimales. Matematicas. Problemas de razones - Parte I. Problemas de razones - Parte II. Problemas de razones - Parte III. Propiedades de las proporciones - HD. Ejercicios de proporciones. Expresiones algebraicas. Operaciones con monomios y polinomios ejercicios. Operaciones con monomios. Polinomios y monomios. Introducción al Algebra - Monomios y Polinomios. Álgebra - Productos notables. Álgebra: Productos notables. Sabemos que se llama producto al resultado de una multiplicación.

También sabemos que los valores que se multiplican se llaman factores. Se llama productos notables a ciertas expresiones algebraicas que se encuentran frecuentemente y que es preciso saber factorizarlas a simple vista; es decir, sin necesidad de hacerlo paso por paso. Se les llama productos notables (también productos especiales) precisamente porque son muy utilizados en los ejercicios. A continuación veremos algunas expresiones algebraicas y del lado derecho de la igualdad se muestra la forma de factorizarlas (mostrada como un producto notable). Productos notables. Productos notables. Binomio al cuadrado Binomio de suma al cuadrado Un binomio al cuadrado (suma) es igual es igual al cuadrado del primer término, más el doble producto del primero por el segundo más el cuadrado segundo.
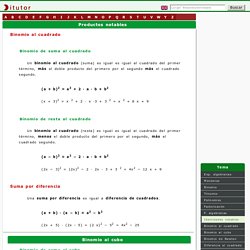
(a + b)2 = a2 + 2 · a · b + b2. Binomio al cuadrado. Binomio al cubo. Álgebra - Ecuaciones. Ecuación. Ecuaciones. Ecuacion de primer grado con denominador. Sistemas de ecuaciones. Sistemas de ecuaciones. Resolver un sistema de ecuaciones consite en encontrar los valores desconocidos de las variables que satisfacen todas las ecuaciones.
Estudiaremos la resolución de los siguientes tipos de sistemas: Sistemas de dos ecuaciones con dos incógnitas. Sistemas de tres ecuaciones con tres incógnitas. Sistemas de ecuaciones no lineales. Método de sustitución 1 Se despeja una incógnita en una de las ecuaciones. 2 Se sustituye la expresión de esta incógnita en la otra ecuación, obteniendo un ecuación con una sola incógnita. 3 Se resuelve la ecuación. 4 El valor obtenido se sustituye en la ecuación en la que aparecía la incógnita despejada. 5 Los dos valores obtenidos constituyen la solución del sistema.
Ejemplo 1 Despejamos una de las incógnitas en una de las dos ecuaciones. 2 Sustituimos en la otra ecuación la variable x, por el valor anterior: 3 Resolvemos la ecuación obtenida: 4 Sustituimos el valor obtenido en la variable despejada. 5 Solución. Relaciones y funciones.