

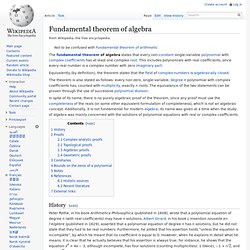
Technology. Elements. Conformal geometry. Fundamental theorem of calculus - Wikipedia, the free ... Polygamma function. Graphs of the polygamma functions ψ, ψ(1), ψ(2) and ψ(3) of real arguments In mathematics, the polygamma function of order m is a meromorphic function on ℂ and defined as the (m + 1)th derivative of the logarithm of the gamma function: Thus holds where ψ(z) is the digamma function and Γ(z) is the gamma function.
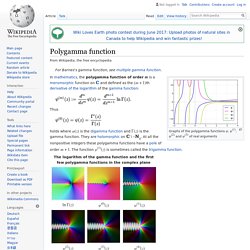
They are holomorphic on ℂ \ −ℕ0. List of unsolved problems in physics. Some of the major unsolved problems in physics are theoretical, meaning that existing theories seem incapable of explaining a certain observed phenomenon or experimental result.
The others are experimental, meaning that there is a difficulty in creating an experiment to test a proposed theory or investigate a phenomenon in greater detail. There are still some deficiencies in the Standard Model of physics, such as the origin of mass, the strong CP problem, neutrino oscillations, matter–antimatter asymmetry, and the nature of dark matter and dark energy.[1][2] Another problem lies within the mathematical framework of the Standard Model itself—the Standard Model is inconsistent with that of general relativity, to the point that one or both theories break down under certain conditions (for example within known spacetime singularities like the Big Bang and the centers of black holes beyond the event horizon).
Unsolved problems by subfield[edit] General physics/quantum physics[edit] Euler's formula. This article is about Euler's formula in complex analysis.
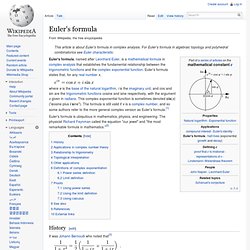
For Euler's formula in algebraic topology and polyhedral combinatorics see Euler characteristic. Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that, for any real number x, Euler's formula is ubiquitous in mathematics, physics, and engineering. Linear algebra - Wikipedia. Branch of mathematics In three-dimensional Euclidean space, these three planes represent solutions of linear equations, and their intersection represents the set of common solutions: in this case, a unique point.

Matrix (mathematics) Two-dimensional array of numbers with specific operations The m rows are horizontal and the n columns are vertical. Binomial theorem. Simpson's paradox. Pascal's law. Pascal's law or the principle of transmission of fluid-pressure is a principle in fluid mechanics that states that pressure exerted anywhere in a confined incompressible fluid is transmitted equally in all directions throughout the fluid such that the pressure variations (initial differences) remain the same.[1] The law was established by French mathematician Blaise Pascal.[2] Definition[edit] Pressure in water and air.
Pascal's law applies only for fluids. Krshort. Khan Academy. Www.cleavebooks.co.uk/trol/trolna.pdf. Fundamental theorem of algebra. The fundamental theorem of algebra states that every non-constant single-variable polynomial with complex coefficients has at least one complex root.
This includes polynomials with real coefficients, since every real number is a complex number with zero imaginary part. History[edit] Peter Rothe, in his book Arithmetica Philosophica (published in 1608), wrote that a polynomial equation of degree n (with real coefficients) may have n solutions. Albert Girard, in his book L'invention nouvelle en l'Algèbre (published in 1629), asserted that a polynomial equation of degree n has n solutions, but he did not state that they had to be real numbers. Furthermore, he added that his assertion holds “unless the equation is incomplete”, by which he meant that no coefficient is equal to 0.
Where α is the square root of 4 + 2√7. A first attempt at proving the theorem was made by d'Alembert in 1746, but his proof was incomplete. Proofs[edit] when |z| > R. Complex-analytic proofs[edit] and let. E (mathematical constant) Functions f(x) = ax are shown for several values of a. e is the unique value of a, such that the derivative of f(x) = ax at the point x = 0 is equal to 1.
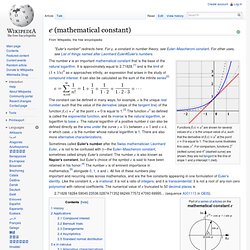
The blue curve illustrates this case, ex. For comparison, functions 2x (dotted curve) and 4x (dashed curve) are shown; they are not tangent to the line of slope 1 and y-intercept 1 (red). 2.71828182845904523536028747135266249775724709369995... Minkowski space. In theoretical physics, Minkowski space is often contrasted with Euclidean space.
While a Euclidean space has only spacelike dimensions, a Minkowski space also has one timelike dimension. Hilbert space. The state of a vibrating string can be modeled as a point in a Hilbert space.
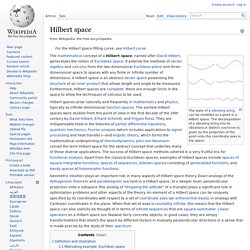
The decomposition of a vibrating string into its vibrations in distinct overtones is given by the projection of the point onto the coordinate axes in the space. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as infinite-dimensional function spaces. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer)—and ergodic theory, which forms the mathematical underpinning of thermodynamics. Tetration. , for n = 1, 2, 3 ..., showing convergence to the infinite power tower between the two dots of infinite power tower converges for the bases In mathematics, tetration (or hyper-4) is the next hyper operator after exponentiation, and is defined as iterated exponentiation.
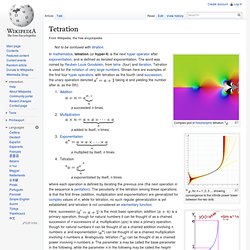
The word was coined by Reuben Louis Goodstein, from tetra- (four) and iteration. Kepler conjecture. The Kepler conjecture, named after the 17th-century German mathematician and astronomer Johannes Kepler, is a mathematical conjecture about sphere packing in three-dimensional Euclidean space. It says that no arrangement of equally sized spheres filling space has a greater average density than that of the cubic close packing (face-centered cubic) and hexagonal close packing arrangements. The density of these arrangements is slightly greater than 74%. Hyperbolic geometry. Lines through a given point P and asymptotic to line R. A triangle immersed in a saddle-shape plane (a hyperbolic paraboloid), as well as two diverging ultraparallel lines. In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai–Lobachevskian geometry) is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced.
The parallel postulate in Euclidean geometry is equivalent to the statement that, in two-dimensional space, for any given line R and point P not on R, there is exactly one line through P that does not intersect R; i.e., that is parallel to R. In hyperbolic geometry there are at least two distinct lines through P which do not intersect R, so the parallel postulate is false. Models have been constructed within Euclidean geometry that obey the axioms of hyperbolic geometry, thus proving that the parallel postulate is independent of the other postulates of Euclid.
Non-intersecting lines[edit] . Triangles[edit] . Euclidean algorithm. Euclid's method for finding the greatest common divisor (GCD) of two starting lengths BA and DC, both defined to be multiples of a common "unit" length. The length DC being shorter, it is used to "measure" BA, but only once because remainder EA is less than CD. Derivative. The graph of a function, drawn in black, and a tangent line to that function, drawn in red.
Parabola. The parabola has many important applications, from a parabolic antenna or parabolic microphone to automobile headlight reflectors to the design of ballistic missiles. Cardioid. Cosine. Sine. Tangent. Tangent to a curve. Solution of the Poincaré conjecture. By contrast, neither of the two colored loops on this torus can be continuously tightened to a point. Fractional quantum Hall effect. Quantum nonlocality. Quantum nonlocality is the phenomenon by which the measurements made at a microscopic level necessarily refute one or more notions (often referred to as local realism) that are regarded as intuitively true in classical mechanics. Rigorously, quantum nonlocality refers to quantum mechanical predictions of many-system measurement correlations that cannot be simulated by any local hidden variable theory. Many entangled quantum states produce such correlations when measured, as demonstrated by Bell's theorem.
Experiments have generally favoured quantum mechanics as a description of nature, over local hidden variable theories.[1][2] Any physical theory that supersedes or replaces quantum theory must make similar experimental predictions and must therefore also be nonlocal in this sense; quantum nonlocality is a property of the universe that is independent of our description of nature. Example[edit] Imagine two experimentalists, Alice and Bob, situated in separate laboratories.
And P(b0|A1) = Holographic principle. Cornell University Library. ArXiv.org e-Print archive. The template Flower of Life. Stanford Lectures. 8.01 Physics I: Classical Mechanics, Fall 1999. Sieve of Eratosthenes. Quadratic equation. Radius of convergence. Imaginary unit.
Complex number. Fourier transform. Complex plane. Avogadro constant. Euler's formula. Gauss–Seidel method.