

Les Graphes. Graphes pondérés. Cours à trou Cours complété Plan de Travail Corrections annales Bac du plan de travail :
Graphes probabilistes. Graphes probabilistes matrices de transition. Graphes définition. MATRICES ET GRAPHES - Transformer une matrice en graphe - Maths Expertes. MATRICES ET GRAPHES - Transformer un graphe en matrice - Maths Expertes. Physique et Maths - Terminale générale - Matrices et graphes. Matrices graphes fiche cours. Indice de Fitting. Les tutos de la prépa: méthode de Newton pour la décomposition polaire par Antoine 1. [LP#10] Le khôlleur fou !
Graphes en série ES (spécialité)
Théorie des graphes. Un article de Wikipédia, l'encyclopédie libre.
La théorie des graphes est une théorie informatique et mathématique. Les algorithmes élaborés pour résoudre des problèmes concernant les objets de cette théorie ont de nombreuses applications dans tous les domaines liés à la notion de réseau (réseau social, réseau informatique, télécommunications, etc.) et dans bien d'autres domaines (par exemple génétique) tant le concept de graphe, à peu près équivalent à celui de relation binaire (à ne pas confondre donc avec graphe d'une fonction), est général.
De grands théorèmes difficiles, comme le théorème des quatre couleurs, le théorème des graphes parfaits, ou encore le théorème de Robertson-Seymour, ont contribué à asseoir cette matière auprès des mathématiciens, et les questions qu'elle laisse ouvertes, comme la conjecture d'Hadwiger, en font une branche vivace des mathématiques discrètes. Définition de graphe et vocabulaire[modifier | modifier le code] et. Parcours de graphes. Introduction aux graphes et leurs structures de données — Algorithmique Avancée. Graphes: quelques définitions Qu’y a t’il de commun entre tous nos problèmes?

Dans chacun d’entre eux, la résolution se ramènera à étudier comment certains objets sont reliés entre eux. Autrement dit, le problème va pouvoir être modélisé à l’aide d’un graphe. Informellement: un graphe est la donnée d’un ensemble de sommets reliés par des arêtes. Voilà un exemple avec neuf sommets. From graph_networkx import GraphG = Graph(nodes=[1, 2, 3, 4, 5], edges=[ (1,2), (1,3), (2,4), (3,4), (4,5) ])G.show() La définition formelle la plus simple est la suivante:
Théorie des graphes. Accomp graphes ES. Graphes. GRAPHES.FR : Théorie des Graphes. Théorie des graphes. ChronoMath, une chronologie des MATHÉMATIQUESà l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Initiée par Euler, avec le célèbre problème des 7 ponts de Königsberg, les applications de la théorie des graphes et de la recherche opérationnelle sont aujourd'hui immenses tant au plan civil que militaire : aide à la décision, stratégie, optimisation (plus court chemin, GPS, coût minimal), réseaux de transports : chemins de fer, métropolitain, lignes aériennes, électricité, gaz, oléoducs (transport de l'énergie), Internet (réseau de l'information), ports et aéroports, ordonnancement des tâches, etc.

La théorie des graphes n'est pas une branche indépendante des mathématiques, elle se rattache à la programmation linéaire, la programmation convexe (où le concept plus général de fonction convexe remplace les fonctions linéaires et affines), la topologie, le calcul des probabilités. Contemporains de Berge, R. Faure et A. Kaufmann en France, F. ! ! ! Utilitaire graphviz. À la découverte des algorithmes de graphe. Ce tutoriel va vous expliquer ce qu'est un graphe, et à quoi il sert.
Il détaillera les algorithmes de graphe les plus courants, en indiquant leur complexité en temps et en mémoire, avec peut-être des schémas si vous êtes sages. Chaque algorithme sera accompagné d'un pseudo-code pour laisser au programmeur l'opportunité de le coder dans son langage favori. Le cours est ouvert aux contributions : vous pouvez m'envoyer une implémentation de l'algorithme dans le langage de votre choix et je l'y ajouterais. Il sera appuyé d'exemples concrets pour que l'intérêt de chaque algorithme apparaisse dans une situation courante.
L'objectif est d'apprendre à reconnaître des problèmes de graphe, ou à modéliser un problème sous forme de graphe, pour le résoudre avec des outils éprouvés et efficaces. Ce document n'a pas pour ambition de faire une démonstration formelle de la complexité ou de la validité des algorithmes. Algorithmique et Graphes. Les graphes : vocabulaire - Maths - Terminale ES spé - Les Bons Profs. Kevin Perrot - Home page. Cher-e-s étudiant-e-s, INFORMEZ-VOUS !

Augmentation des frais d'inscription à l'université: Pas en mon nom (article Mediapart) Réforme Macron-Philippe des retraites: C'est quand qu'on arrête ? (bande-dessinée par Emma) Décryptage de Michael Zemmour (vidéo) Loi de Programmation Pluriannuelle de la Recherche (LPPR): Expliquée par Antoine Gaudin (vidéo) A note on Computability Theory including a video of the Lego Turing machine!
M2 Info Maths Dscirètes - MOdèles de CAlcul NAturels - AMU Avec Giuseppe Di Molfetta et Antonio E. Code Python et jeux de données. Index of /option-mpsi/pdf. Index of /licence3/Graphes. Graphes pour Tle ES. Chapitre 1. Chapitre 2. Graphes et algorithmes des graphes (bouchitte) Algorithmes sur les graphes. Il est conseillé de relire au moins une fois le cours consacré aux graphes.

Nous allons commencer par nous intéresser aux algorithmes de parcours d'un graphe. L'idée du "parcours" est de "visiter" tous les sommets d'un graphe en partant d'un sommet quelconque. Ces algorithmes de parcours d'un graphe sont à la base de nombreux algorithmes très utilisés : routage des paquets de données dans un réseau, découverte du chemin le plus court pour aller d'une ville à une autre... Il existe 2 méthodes pour parcourir un graphe : Le parcours en largeur d'abord le parcours en profondeur d'abord le parcours en largeur d'abord Nous allons travailler sur un graphe G(V,E) avec V l'ensemble des sommets de ce graphe et E l'ensemble des arêtes de ce graphe.
Si u.couleur = blanc => u n'a pas encore été "découvert" si u.couleur = noir => u a été "découvert"
Algorithmes sur les graphes. GRAPHES. La théorie des graphes est un bel exemple de théorie mathématique collée à la réalité depuis son origine.
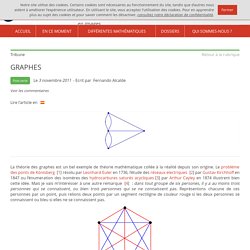
Le problème des ponts de Könisberg [1] résolu par Leonhard Euler en 1736, l’étude des réseaux electriques [2] par Gustav Kirchhoff en 1847 ou l’énumeration des isomères des hydrocarbures saturés acycliques [3] par Arthur Cayley en 1874 illustrent bien cette idée. Mais je vais m’intéresser à une autre remarque [4] : dans tout groupe de six persones, il y a au moins trois personnes qui se connaissent, ou bien trois personnes qui se ne connaissent pas. Représentons chacune de ces personnes par un point, puis relions deux points par un segment rectiligne de couleur rouge si les deux personnes se connaissent ou bleu si elles ne se connaissent pas.
La remarque devient alors un théorème, appelé théorème de Ramsey, qu’on peut reformuler de la façon suivante : le graphe bicoloré G ainsi obtenu [5] contient soit un triangle rouge, soit un triangle bleu. En réalité, Frank P. GRAPHES 1. Nous sommes en 2718 sur la planète Terre, une des planètes du système solaire.
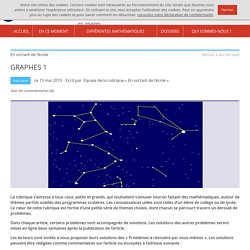
Le fameux professeur Euler, terrien d’origine, doit se rendre sur la planète Mars pour initier un groupe d’étudiants martiens à la théorie des graphes. Un réseau de navettes spatiales entre les planètes du système solaire, y compris les naines, vient juste de se mettre en place. Le professeur Euler se présente alors au terminal des navettes de la planète Terre afin d’organiser son voyage vers Mars. Il découvre que seules les liaisons suivantes fonctionnent : Terre-Vénus, Mars-Jupiter, Uranus-Saturne, Cérès-Pluton, Saturne-Jupiter, Pluton-Hauméa, Vénus-Mercure, Mercure-Terre, Mars-Neptune, Cérès-Éris, Hauméa-Makémaké, Neptune-Uranus, Cérès-Hauméa et Saturne-Neptune.
Le professeur Euler griffonne quelques notes sur son carnet et conclut très vite qu’il ne pourra se rendre sur Mars. GRAPHES 2. Des arbres Piste bleue Le 28 juin 2015 - Ecrit par Equipe de la rubrique « En sortant de l’école » La rubrique s’adresse à tous ceux, petits et grands, qui souhaitent s’amuser tout en faisant des mathématiques, autour de thèmes parfois oubliés des programmes scolaires.
Les connaissances utiles sont celles d’un élève de collège ou de lycée. Le cœur de cette rubrique est formé d’une petite série de thèmes choisis, dont chacun se parcourt travers un déroulé de problèmes. Dans chaque article, certains problèmes sont accompagnés de solutions. GRAPHES 3. Le professeur Euler retrouve ses étudiants martiens pour la troisième fois (une première fois ici, une deuxième là).
Son objectif est de leur présenter une formule que l’on attribue à son fameux aïeul Leonhard Euler, la formule d’Euler, que Descartes avait approchée avant lui. Cette formule concerne un certain type de graphes que l’on dit planaires. Le professeur Euler revient tout d’abord sur quelques notions qu’il a développées lors de ses deux premières leçons. LE DÉCOUPAGE DES GRAPHES. Un virus se balade sur le réseau local de mon établissement.
Seule thérapie : couper les connexions entre ordinateurs sains et ordinateurs infectés. Combien y a t-il de connexions à couper, dans le pire des cas ? Le calcul exact de ce nombre pour de grands réseaux est difficile. On sait le faire à 87.85672057848516% près, mais pas à 87.85672057848517% près. On dirait une curiosité mathématique. Contagion. GRAPHIQUE TROMPEUR. Cette note est une petite remarque de mathématiques élémentaires, suscitée par un graphique édité par une banque. La valeur en bourse des banques, leur « capitalisation boursière » s’effondre depuis quelques dizaines de mois. La banque américaine JP Morgan propose une représentation de cet effondrement, depuis le deuxième trimestre 2007. GRAPHIQUES FRELATÉS. Le 17 mars 2012 - Ecrit par Étienne Ghys Peut-on imaginer un graphique plus dénué d’intérêt que celui qu’on trouve ce 10 mars dans Libération ?
Cliquer pour agrandir Observons que : Le résultat d’un sondage devrait toujours être assorti d’une marge d’erreur. Pour un sondage portant sur un millier de personnes cette marge est de quelques pourcents. Un autre exemple, plus malhonnête encore ? Les rectangles roses représentent en principe les pourcentages de 41,9%, 45,5%, 48,8% et 56,2%. DES GRAPHES À COURBURE POSITIVE. Dans son billet, Christian Bonatti écrivait qu’il y a sûrement des sujets mathématiques assez difficile à vulgariser, prenant comme exemple le thème du séminaire auquel il avait assisté la veille. Il terminait en lançant une sorte de défi : en faisant un effort, on doit bien y arriver...
Allez, chiche ! Une fois par mois, j’essaie de vous raconter un des derniers exposés auxquels j’ai assisté. Lucas Gerin : Enseignements. #3. Les graphes (5 min. pour comprendre) Les graphes, pour quoi, pour qui, et pourquoi pas pour des collégiens ? Pourquoi ce titre et comment est née cette idée de créer un article sur le sujet ? La première année du changement de programme de terminale ES en 2002, j’ai eu l’opportunité de corriger des copies de terminale ES spécialité mathématiques lors d’un bac blanc.
Créer un graphe en ligne et trouver le plus court chemin ou appliquer d'autres algorhtmes. À la découverte des graphes. Graphes non orientés. En entreprise, certains problèmes d’affectation apparaissent comme de vrais casse-têtes lorsqu’on cherche à les résoudre sans méthode. Culture algorithmique - Vidéo Spécialités. Il existe beaucoup de structures de données complexes en informatique : la liste, les listes doublement chaînées, les piles et files qui servent notamment à stocker des tâches à effectuer, les tables de hachage pour représenter des ensembles, des arbres et des tas qui sont des structures plus compliquées, avec beaucoup de structures sous-jacentes, les graphes et les bases de données.
Graphe eulerien. Parcours eulériens. Dans les années 1730, Leonhard Euler chercha à résoudre un problème pratique. Graphes orientés. Les graphes orientés sont enseignés en terminale ES spé math et dans plusieurs cursus du supérieur. Cette page introduit cet outil mathématique et le vocabulaire qui lui est lié, parfois différent de celui des graphes non orientés. Précisons au passage que les arbres de probabilités et les organigrammes sont eux aussi des graphes orientés. Graphes et matrices. On trouve les matrices dans des applications particulièrement variées. Introduction aux graphes probabilistes. En terminale générale maths expertes, on étudie plusieurs types de graphes afin de résoudre divers problèmes d’optimisation.
Exercices sur les graphes non orientés. L’exercice de spécialité de l’épreuve du bac ES de juin 2017 en Amérique du nord s’avère être un très bon exercice sur les graphes non orientés. Alors sans plus attendre, voici le sujet. Le corrigé suit mais bien sûr, si vous vous précipitez dessus, vous ne vous serez pas entraîné.
Créer un graphe en ligne et trouver le plus court chemin ou appliquer d'autres algorhtmes. Graphes : introduction et notions de base.
9 ntsGraphes. Geoboard by The Math Learning Center. Marche de l'ivrogne, évolution des espèces. Théorème des quatre couleurs via les graphes. Graphes - UQAC. Les graphes. Graphes planaires. #3. Les graphes (5 min. pour comprendre) Math Park - 10/05/2014 - Aline Parreau, voyage au pays des graphes. Cours Graphes IREM. TES specialite.tex.
Graph24. Arbres et chemins. Graph theory. GrapheNotes. M2 Fouille de données. CM SEQ AMI. Fouille de graphes jsf2012. CoursIndexationLIF10. Representation connaissance2. Cours-Graphes Aléatoires-online.pdf. Graphes RW 2014. Algorithmique des graphes. Modèles et Algorithmes de Graphe. Catégorie:Théorie des graphes. GraphTheory Techniques In Model Based Testing. Les graphes planaires. Arbres. Arbres binaires de recherche. Arbre de Stern-Brocot.
Algorithm — En quoi un arbre couvrant un goulot d'étranglement minimum est-il différent d'un arbre couvrant minimum?
Arbres gloutons. Arbres k-d. Théorème de Kruskal et des arbres, LMSB#5. Graphes orientés. Orientation graphe. Ordre topologique : dessiner un graphe orienté de la gauche vers la droite. Graphique médian.