

Biographie de Niels Abel. La vie de Niels Abel, mathématicien norvégien né le 5 août 1802, est marquée par la pauvreté.

Son père était pourtant un éminent homme politique norvégien, mais à la fin de sa vie il est tombé en disgrâce, et quand il meurt en 1820, c'est Abel qui doit supporter la charge de la famille. Grâce à l'aide financière de ses professeurs, il parvient cependant à poursuivre ses études et à faire ses premières découvertes. Mais ses mémoires sont perdus par Cauchy, mésestimés par Gauss. Après son doctorat, Abel ne parvient pas à trouver un poste, ses conditions de vie sont de plus en plus précaires et sa santé se fait fragile : il est atteint de la tuberculose. Théorème d'Abel (algèbre) Tous les corps considérés dans cet article sont supposés commutatifs et de caractéristique nulle[1].
Niels Henrik Abel (1802-1829) présente la première démonstration rigoureuse et complète du théorème qui porte maintenant son nom. Des méthodes numériques comme la méthode de Newton ou celle de Laguerre s'appliquent indépendamment du degré de l'équation. Si n, le degré du polynôme, est petit, il existe aussi des méthodes dites algébriques pour résoudre l'équation. Ainsi, si n est égal à 2, et si P s'écrit aX2 + bX + c, les solutions sont données par la formule classique (–b ± √b2 – 4ac)/2a, où b2 – 4ac est le discriminant du polynôme ; on dit que √b2 – 4ac est un radical. Des formules analogues (mais plus compliquées) existent pour les polynômes de degré 3 ou 4, comme le montrent les méthodes de Cardan et de Ferrari. L'expression utilisée par Abel dans son mémoire de 1824[2] est la suivante : Abel : malchanceux à vie. Niels Henrik Abel naît le 5 août 1802 à Frindoë (près de Stavanger).

Sa vie fut marquée par la malchance : son père est un célèbre homme politique mais il tombe en disgrâce. Sa famille se trouve alors en difficulté quand il meut en 1820. Niels parvient cependant à étudier, aidé financièrement par ses professeurs, mais ses mémoires sont perdus (Cauchy) ou méprisés (Gauss). Ne parvenant pas à trouver un poste après son doctorat, ses conditions de vie se détériorent et il est atteint de tuberculose. Il décède le 5 avril 1829, âgé de seulement 26 ans, alors qu'un poste à Berlin s'offrait à lui. Abel Niels Henrik. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Niels Abel fit ses études au collège de la cathédrale d'Oslo (Christiania à l'époque) jusqu'en 1821.

Dès l'âge de 16 ans, il découvre les œuvres de Euler et de Lagrange et cherche à résoudre l'équation du 5ème degré; mais ses maîtres ne prêtèrent pas attention à ses recherches. Il s'attaqua alors aux intégrales elliptiques tout en continuant à travailler sur les équations algébriques. Il entre ensuite à l'université d'Oslo où il présentera (1824) ses premiers résultats sur l'équation du 5ème degré confirmés par Ruffini qui travaillait indépendamment sur le sujet. Grace à une bourse d'études, il se rend à Berlin (1825); il y rencontre Crelle et malgré ses publications dans le journal de ce dernier, les travaux de ce jeune et génial mathématicien laissent indifférente la communauté mathématique. Nombres algébriques, entiers algébriques :
Niels Abel et les critères de convergence. Niels Henrik Abel. Tout comme Galois, Niels Henrik Abel s’est intéressé très jeune au problème de la résolution des équations du cinquième degré, mais il s’est également intéressé aux fonctions elliptiques.

Tout comme Galois, il est mort très jeune sans avoir eu le temps de réaliser ses ambitions. Galois est mort dans les bras de son jeune frère, Abel dans les bras de sa fiancée. Niels Henrik Abel est un mathématicien norvégien né le 5 août 1802, à Frindoë près de Stavanger. Il est connu pour ses travaux en analyse mathématique sur la semiconvergence des séries numériques, des suites et séries de fonctions, sur les critères de convergence d’intégrale généralisée et sur la notion d’intégrale elliptique; en algèbre, sur la résolution des équations.
Abel, deuxième d’une famille de sept enfants, passa ses premières années dans un pays frappé par la famine du fait du blocus continental, Napoléon ayant contraint les couronnes de Norvège et du Danemark à rejoindre sa coalition contre l’Angleterre. Ackermann Wilhelm. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Élève de Hilbert à Göttingen, Ackermann obtient son doctorat en 1925.

Sa thèse et ses recherches portent sur la logique mathématique et la consistance des systèmes formels, une des questions mathématiques majeures du début du 20è siècle. Il s'agit de rechercher si un système d'axiomes d'une théorie ne contient pas des règles contradictoires et de développer un nouveau langage mathématique échappant au domaine trop intuitif de la logique traditionnelle du tiers exclu héritée d'Aristote. Cette logique qui avait fait preuve de grave insuffisance depuis l'apparition des premières contradictions nées de la théorie des ensembles de Cantor. Pour qualifier ces travaux sur les fondements des mathématiques, s'attachant à une théorie de la démonstration, on parle de métamathématique (terme initié par Hilbert).
Axiome de Boll : Wilhelm Ackermann. Fonction d'Ackermann. Dans la théorie de la récursivité, la fonction d'Ackermann (aussi appelée fonction d'Ackermann-Péter) est un exemple simple de fonction récursive non récursive primitive, trouvée en 1926 par Wilhelm Ackermann.
Elle est souvent présentée sous la forme qu'en a proposée la mathématicienne Rózsa Péter, comme une fonction à deux paramètres entiers naturels comme arguments et qui retourne un entier naturel comme valeur, noté en général A(m, n). Histoire[modifier | modifier le code] Dans les années 1920, Wilhelm Ackermann et Gabriel Sudan, alors étudiants sous la direction de David Hilbert, étudiaient les fondements de la calculabilité. Sudan est le premier à donner un exemple de fonction récursive mais non récursive primitive, appelée alors fonction de Sudan.
Peu après et indépendamment, en 1928, Ackermann a publié son propre exemple de fonction récursive mais non récursive primitive[1]. Index of /master1/mi1-tc5/SOURCES/ACKERMANN. Gérard Patrick - "D'Alembert : les Lumières et les ondes" - 2013. Réalisation BnF.
Jean le Rond D'Alembert est surtout connu pour son rôle de rédacteur de l'Encyclopédie, et peut-être un peu moins comme mathématicien. Né le 16 novembre 1717 à Paris, des amours illégitimes entre une femme de lettres et un chevalier artilleur, il est abandonné dès sa naissance sur les marches de la chapelle Saint-Jean-le-Rond, ce qui lui valut son prénom, puis retrouvé par son père, qui veillera sur lui sans toutefois le reconnaître. Il est finalement confié à une nourrice qui en prendra soin une grande partie de sa vie. Après de brillantes études, il présente à l'Académie des Sciences de Paris son premier travail mathématique à l'âge de 22 ans.
DOSSIER : JEAN LE ROND D’ALEMBERT. Maria Gaetana Agnesi. Maria Gaetana Agnesi.
Maria Gaetana Agnesi, née à Milan (Italie) le 16 mai 1718 et morte le 9 janvier 1799 dans sa ville natale, est une mathématicienne italienne. Elle a écrit un traité d'analyse mathématique renommé pour sa clarté et l'unité de sa méthode[1]. Un ouvrage de philosophie est également paru sous son nom alors qu'elle avait neuf ans ; elle présente un discours, en latin, sur le droit des femmes à l'éducation. Nommée à l'université de Bologne par le pape Benoît XIV[note 1], mais elle n'y a jamais enseigné.
Délaissant la science après la mort de son père, elle a consacré toute la seconde partie de sa vie à « servir Dieu ainsi que le prochain[2] ». Marie Gaetana Agnesie. Agnesi. Agnesi. Sorcière d'Agnesi. Un article de Wikipédia, l'encyclopédie libre.
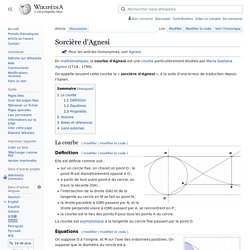
En mathématiques, la courbe d'Agnesi est une courbe particulièrement étudiée par Maria Gaetana Agnesi (1718 - 1799). On appelle souvent cette courbe la « sorcière d'Agnesi », à la suite d'une erreur de traduction depuis l'italien. La courbe[modifier | modifier le code] Définition[modifier | modifier le code] Elle est définie comme suit : sur un cercle fixe, on choisit un point O ; le point M est diamétralement opposé à O ;à partir de tout autre point A du cercle, on trace la sécante [OA) ;l'intersection de la droite (OA) et de la tangente au cercle en M se fait au point N ;la droite parallèle à (OM) passant par N, et la droite perpendiculaire à (OM) passant par A, se rencontrent en P ;la courbe est le lieu des points P pour tous les points A du cercle.
Lars Valerian Ahlfors. Lars Ahlfors. Lars Valerian Ahlfors est un mathématicien finlandais né en 1907 à Helsingfors (Helsinki aujourd'hui) et mort en 1996 dans le Massachusetts, aux États-Unis. Il a reçu la première médaille Fields en 1936. Ahlfors Lars. ChronoMath, une chronologie des MATHÉMATIQUES à l'usage des professeurs de mathématiques, des étudiants et des élèves des lycées & collèges Source portrait : MFO, Oberwolfach Photo collectionSource biographique : Acad. des sciences US : » Réf. 1.
D'Alembert, abandonné à la naissance. Jean Le Rond d'Alembert naît le 16 novembre 1717 à Paris mais c'est un enfant illégitime. Il est ainsi abandonné sur le parvis de l'église Jean Le Rond, d'où son prénom, et recueilli par une femme de vitrier. Il vit avec elle jusqu'à ce qu'elle meurt ; il a alors 48 ans. Il reçoit secrètement de l'argent de son père et entre dans un collège janséniste en 1729. Il étudie ensuite le droit et la médecine mais s'intéresse surtout aux mathématiques. Il publie des mémoires sur la mécanique des fluides (1743) et le calcul intégral (1739), ce qui lui vaut d'entrer à l'Académie des Sciences le 29 mai 1741 en tant qu'associé astronome adjoint.
Ses découvertes sont importantes : citons la première résolution des équations aux dérivées partielles concernant la propagation des ondes sonores et un début de solution au problème des trois corps (ce problème consiste à étudier le mouvement de trois corps agissant les uns sur les autres par gravité). Jean Le Rond d'Alembert. Signature Jean Le Rond d'Alembert[a], parfois écrit « Jean le Rond D’Alembert[b],[c] » est un mathématicien, physicien, philosophe et encyclopédiste français, né le 16 novembre 1717 à Paris où il est mort le 29 octobre 1783. Il est célèbre pour avoir été l'inventeur d'un principe de l'équilibre que Condorcet explique dans son Éloge de d'Alembert[1]. Il a ainsi fixé une liaison entre les lois du mouvement. Par son théorème maintenant nommé « théorème d'Alembert », il perçoit la présence de « n » racines dans toute équation algébrique de degré « n ».
En 1744, il est l'inventeur de cette nouvelle branche des mathématiques, le calcul aux dérivées partielles, qui introduit des fonctions arbitraires. Biographie de Jean Le Rond d'Alembert. D'Alembert et les équations aux différences partielles. Théorème fondamental de l'algèbre. Jean Le Rond D’Alembert (1717-1783) LES LUMIÈRES ET LES ONDES. Gérard Patrick - "D'Alembert : les Lumières et les ondes" - 2013. La résolution des équations aux dérivées partielles dans les Opuscules mathématiques de D’Alembert (1761-1783) RHM 2009 15 1 59 0. Alexandrov Pavel Sergueïevitch. Ibn al-Hassan ibn al-Haytam (Alhazen) Biographie de Jamshid al-Kashi. Al Kashi. A cette époque, les scientifiques effectuent leurs recherches à la cours de rois ou de princes. A Samarkand, al Kashi vit sous la protection du prince Ulugh-Beg (1394 ; 1449) qui a fondé une Université comprenant une soixantaine de scientifiques qui étudient la théologie et les sciences.
Al-kashi. Ce résultat est porte le nom du mathématicien persan du début du XVe siècle al-Kâshî. Al-Kashi. Al Kashi. Al Kashi) □ Al Kashi, plus fort que Pythagore ? / Maths C qui ? #8. Al Kashi et formule des sinus. Le théorème d'Al Kashi (Trigonométrie XIX) Al-Khwârizmî, père de l'algèbre arabe - Fermat Science. Voyage en Mathématique - Ahmed Djebbar - Al-Khwârizmî, père de l'algèbre arabe. L'histoire d'Al-Khwarizmi ou presque... Al Khwarizmi, fondateur des mathématiques arabes. Comment Al Khwarismi résolvait les équations du 1er degré -Al-jabr, al mukkabala, al hatt. Les équations canoniques d’Al-Khawārizmi. Al Kwarizmi. □ Le 2nd degré d'Al Khwarizmi / Maths C qui ? #3. Al khwarizmi. EXCLU IMA : La découverte de l'algèbre par al-Khwarizmi. Al-Khwarizmi, le vrai père de Facebook.
Algorithme Algebre origine : Islam. Nasir al-Din al-Tusi. Nasir ad-Din at-Tusi. Al Tusi. André-Marie Ampère. Apollonius de Perge, appelé le « grand géomètre » Apollonios de Perga. Apollonius de Perge. Apollonius. Cercle d'Apollonius. APOLLONIUS DE PERGIA ET LE TRAITÉ DES CONIQUES. Appell Paul Emile.
Suren Arakelov. Histoire et préhistoire de la Géométrie d'Arakelov. Géométrie d'Arakelov des surfaces arithmétiques. John Arbuthnot.
Biographie de Jean-Robert Argand. Argand Jean Robert. Pour chercher et approfondir - La démonstration par Argand du théorème fondamental de l’algèbre. [CM#2] Quantités imaginaires. Essai sur une manière de représenter des quantités imaginaires dans les constructions géométriques. Biographie et principaux travaux du mathématicien Aristarque. Aristarque de Samos : contredire les platistes en utilisant son cerveau. Aristote. La logique d'Aristote. Vladimir Arnold. Arzela Cesare. Ascoli Giulio. Michael Atiyah. Atiyah-Beauty. Geometry in 2, 3 and 4 Dimensions - Michael Atiyah. Résumé rapide: la "démonstration" de l'hypothèse de Riemann. The Riemann Hypothesis. Sir Michael Atiyah, What is a Spinor ? L'étoile polaire et la fin de vie (élégie pour un ami décédé) Watertoyourmill1 on an idea oh Michael Atiyah. Théorème de van Aubel. Théorème de Van Aubel.