

Algebra Homework Help, Algebra Solvers, Free Math Tutors. Algebra 2 Finals Cheat Sheet Cheat Sheet by justind23. High School Logarithms. Interval Notation. Interval Notation. Parent Functions and Transformations - She Loves Math. This section covers: Note that examples of transformations of Rationals can be found here, and more examples of transformations of Exponential and Log Functions can be found here.
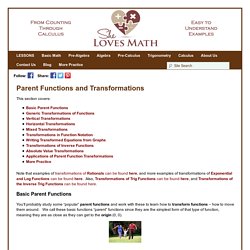
Also, Transformations of Trig Functions can be found here, and Transformations of the Inverse Trig Functions can be found here. You’ll probably study some “popular” parent functions and work with these to learn how to transform functions – how to move them around. We call these basic functions “parent” functions since they are the simplest form of that type of function, meaning they are as close as they can get to the origin (0, 0).
The chart below provides some basic parent functions that you should be familiar with. I know we haven’t covered all these yet (sorry!) You’ll learn about the trigonometric parent functions and transformations here in the Graphs of Trig Functions and Transformations of Trig Functions sections, respectively. Most of the time, our end behavior looks something like this: instead of . ? Reflections of a graph - Topics in precalculus. CONSIDER THE FIRST QUADRANT point (a, b), and let us reflect it about the y-axis.
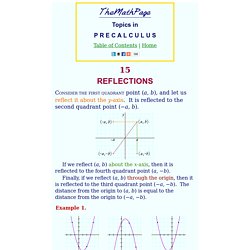
It is reflected to the second quadrant point (−a, b). If we reflect (a, b) about the x-axis, then it is reflected to the fourth quadrant point (a, −b). Finally, if we reflect (a, b) through the origin, then it is reflected to the third quadrant point (−a, −b). The distance from the origin to (a, b) is equal to the distance from the origin to (−a, −b). Example 1. Exponential growth calculator. Exponentials & Logarithms - Cool math Algebra Help Lessons - What's a Logarithm?
Logarithmic and exponential functions - Topics in precalculus. Exponential functions Inverse relations Exponential and logarithmic equations Creating one logarithm from a sum THE LOGARITHMIC FUNCTION WITH BASE b is the function y = logb x. b is normally a number greater than 1 (although it need only be greater than 0 and not equal to 1).
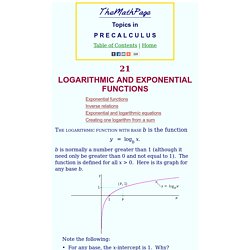
Note the following: • For any base, the x-intercept is 1. To see the answer, pass your mouse over the colored area. The logarithm of 1 is 0. y = logb1 = 0. Logarithmic Functions. The section covers: Half-Life problems can be found here.
What is a Log and Why do we Need Them? I have to admit that logs are one of my favorite topics in math. I’m not sure exactly why, but you can do so many awesome things with them! We’ll soon see that Logs can be used to “get the variable in the exponent down” so we can solve for it. A slide rule was used (among other things) to multiply and divide large numbers by adding and subtracting their exponents. Interactive Logarithm Table.
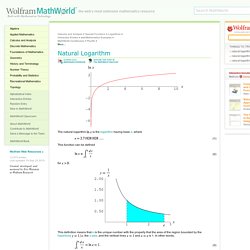
From Wolfram MathWorld. The natural logarithm is the logarithm having base e, where This function can be defined for.
7. Log-Log and Semi-log Graphs. Basic Skill Practice Games. Canada's Number 1 Math Website - Mathletics.ca - Love Learning. Logarithms rules and formula. Product rule, power rule, quotient rule and other formulas for logarithms. Working with Exponents and Logarithms.
What is an Exponent?

What is a Logarithm? A Logarithm goes the other way. It asks the question "what exponent produced this? ": And answers it like this: In that example: The Exponent takes 2 and 3 and gives 8 (2, used 3 times in a multiplication, makes 8) The Logarithm takes 2 and 8 and gives 3 (2 makes 8 when used 3 times in a multiplication) A Logarithm says how many of one number to multiply to get another number So a logarithm actually gives you the exponent as its answer: (Also see how Exponents, Roots and Logarithms are related.) Working Together Exponents and Logarithms work well together because they "undo" each other (so long as the base "a" is the same): They are "Inverse Functions" Doing one, then the other, gets you back to where you started: Doing ax then loga gives you x back again: Doing loga then ax gives you x back again: It is too bad they are written so differently ... it makes things look strange.
Going up, then down, returns you back again:down(up(x)) = x. Logarithms: Introduction to "The Relationship". Purplemath offers a complete lessonon the topic you have selected.Try the lesson below!
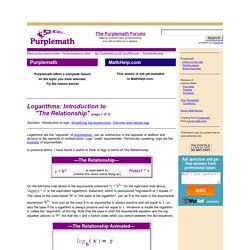
This lesson is not yet availablein MathHelp.com. Logarithms: Introduction to "The Relationship" (page 1 of 3) Sections: Introduction to logs, Simplifying log expressions, Common and natural logs Logarithms are the "opposite" of exponentials, just as subtraction is the opposite of addition and division is the opposite of multiplication. Logs "undo" exponentials. In practical terms, I have found it useful to think of logs in terms of The Relationship:
Logarithmic and exponential functions - Topics in precalculus. Home. LINKS. Esercitiamoci con Geogebra.