

Mike's World-O-Programming - Yet Another Monad Tutorial (part 1: basics) It's a standing joke in the Haskell community that every Haskell programmer, as part of his or her learning process, will eventually write one or more monad tutorials.
I'm certainly no exception. But since I know that there are already dozens of monad tutorials out there, some quite good, why on earth would I want to write Yet Another One? There are two reasons: I think I can explain some aspects of monads better than most of the monad tutorials I've seen.My own understanding of monads has improved greatly, and I'd like to try to pass that on if I can. Prerequisites Since I will be using the programming language Haskell in my examples, it would be very helpful if you, the reader, know Haskell up to and including polymorphic types and type classes. One prerequisite I will not be assuming is any knowledge of category theory, which is a very abstract branch of mathematics where the concept of a monad (as the term is used here) originated.
Disclaimer. Why Do Monads Matter? « Sententia cdsmithus. (A Side Note: I’ve been formulating the final thoughts on this post for about a week now.
In an entirely unrelated coincidence, a good friend of mine and fellow Haskell programmer, Doug Beardsley, ended up writing two posts about monads over the weekend as well. Weird! Learn Haskell Fast and Hard. I really believe all developers should learn Haskell.

I don’t think everyone needs to be super Haskell ninjas, but they should at least discover what Haskell has to offer. Learning Haskell opens your mind. Mainstream languages share the same foundations: variablesloopspointersdata structures, objects and classes (for most) Haskell is very different. But learning Haskell can be hard. This article will certainly be hard to follow. The conventional method to learning Haskell is to read two books. In contrast, this article is a very brief and dense overview of all major aspects of Haskell.
The article contains five parts: Introduction: a short example to show Haskell can be friendly.Basic Haskell: Haskell syntax, and some essential notions.Hard Difficulty Part: Functional style; a progressive example, from imperative to functional styleTypes; types and a standard binary tree exampleInfinite Structure; manipulate an infinite binary tree! 01_basic/10_Introduction/00_hello_world.lhs Introduction. Haskell - A monad is just a monoid in the category of endofunctors, what's the problem. Chapter 2. Types and Functions. Category Theory. Combinations and Permutations. What's the Difference?

In English we use the word "combination" loosely, without thinking if the order of things is important. In other words: So, in Mathematics we use more precise language: In other words: A Permutation is an ordered Combination. Permutations There are basically two types of permutation: Repetition is Allowed: such as the lock above. 1. These are the easiest to calculate. When we have n things to choose from ... we have n choices each time! When choosing r of them, the permutations are: n × n × ...
(In other words, there are n possibilities for the first choice, THEN there are n possibilites for the second choice, and so on, multplying each time.) Which is easier to write down using an exponent of r: n × n × ... Example: in the lock above, there are 10 numbers to choose from (0,1,...9) and we choose 3 of them: 10 × 10 × ... (3 times) = 103 = 1,000 permutations. Haskell/Category theory. This article attempts to give an overview of category theory, in so far as it applies to Haskell.
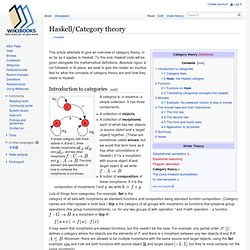
To this end, Haskell code will be given alongside the mathematical definitions. Absolute rigour is not followed; in its place, we seek to give the reader an intuitive feel for what the concepts of category theory are and how they relate to Haskell. Introduction to categories[edit] A simple category, with three objects A, B and C, three identity morphisms. Parsec. This article is a stub.
You can help by expanding it. 1 Introduction Parsec is an industrial strength, monadic parser combinator library for Haskell. It can parse context-sensitive, infinite look-ahead grammars but it performs best on predictive (LL[1]) grammars. The latest stable release with Haddock documentation is available on Hackage and development versions are available via the Darcs repository. 2 Usage Parsec lets you construct parsers by combining higher-order Combinators to create larger expressions. An example for parsing a simple grammar of expressions can be found here. Much more documentation can be found on the parsec website. 3 Examples "Using Parsec" chapter on Real World Haskell.
See also the list of reverse dependencies for Parsec. 4 Parsec clones in other languages Interesting non-Parsec parser combinator libraries: Parse::RecDescent for Perl [15] Spirit for C++ [16] 5 Links 5.1 Docs 5.2 Blog articles Adventures in Parsec by Antoine Latter 5.3 Other.