

Untitled. Sententia cdsmithus. (A Side Note: I’ve been formulating the final thoughts on this post for about a week now.
In an entirely unrelated coincidence, a good friend of mine and fellow Haskell programmer, Doug Beardsley, ended up writing two posts about monads over the weekend as well. Weird! But don’t fret; this isn’t really the same thing at all. I’m not writing to teach Haskell programmers how to use monads. I’m writing about a kind of intuition about why these concepts turn out to matter in the first place. Category Theory for Software Development? Haskell - State and IO Monads. All About Monads. All About Monads is a tutorial on monads and monad transformers and a walk-through of common monad instances.
You can download a PDF version here. And here is a version of the article which includes source code. 1.1 What is a monad? A monad is a way to structure computations in terms of values and sequences of computations using those values. Monads allow the programmer to build up computations using sequential building blocks, which can themselves be sequences of computations. Haskell/Understanding monads/State - Wikibooks, open books for an open world. If you have programmed in any other language before, you likely wrote some functions that "kept state".
For those new to the concept, a state is one or more variables that are required to perform some computation but are not among the arguments of the relevant function. Object-oriented languages, like C++, suggest extensive use of state variables within objects in the form of member variables. Programs written in procedural languages, like C, typically use variables declared outside the current scope to keep track of state. In Haskell, however, such techniques are not as straightforward to apply. They require mutable variables and imply functions will have hidden dependencies, which is at odds with Haskell's functional purity. Pseudo-Random Numbers[edit] Generating actual random numbers is far from easy. Anton-k/monads-for-drummers. How I learned to understand Monads : haskell. LTMT Part 3: The Monad Cookbook. Introduction The previous two posts in my Less Traveled Monad Tutorial series have not had much in the way of directly practical content.
Monads, lifting, join, and side-effecting actions. While playing around with querying ElasticSearch I bumped into something that I hadn’t really understood explicitly before about monads, nesting, and IO.
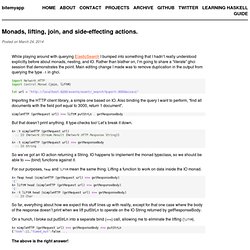
Rather than blather on, I’m going to share a “literate” ghci session that demonstrates the point. Main editing change I made was to remove duplication in the output from querying the type :t in ghci. import Network.HTTPimport Control.Monad (join, liftM) let url = " Importing the HTTP client library, a simple one based on IO. Also binding the query I want to perform, “find all documents with the field port equal to 3000, return 1 document”. simpleHTTP (getRequest url) >>= liftM putStrLn . getResponseBody But that doesn’t print anything.
Λ> :t simpleHTTP (getRequest url) :: IO (Network.Stream.Result (Network.HTTP.Response String)) λ> :t simpleHTTP (getRequest url) >>= getResponseBody :: IO String So we’ve got an IO action returning a String. For our purposes, fmap and liftM mean the same thing. The above is the right answer! IO: You may say I'm a monad, but I'm not the only one! One of the things I love about Haskell is its tools for abstracting computation.

There are so many different ways to look at a given problem, and new ones are being invented/discovered all the time. Monads are just one abstraction, a popular and important one. When you’re learning Haskell, you’re told ’IO is a monad’, and whether or not you understand what that means, you start to see the significance of binding impure values, returning pure ones, using do notation, and so on.
I thought I was a pro at monads after discovering liftM, but I still hadn’t really made the jump to understanding monads in general, rather than as something specific to impure IO operations. So today we’ll take a look at practical uses of the monad-ness of types other than IO: in particular, list and Maybe. Speaking of Applicative and Functor, I’ll also be introducing some of those other computation abstractions, and showing you the same code using several different styles.
You Could Have Invented Monads! (And Maybe You Already Have.) If you hadn't guessed, this is about monads as they appear in pure functional programming languages like Haskell.

They are closely related to the monads of category theory, but are not exactly the same because Haskell doesn't enforce the identities satisfied by categorical monads. Writing introductions to monads seems to have developed into an industry. The Monadic Way. Note Since the size of the previous file was getting too big for a wiki, the tutorial has been divided into two parts: The Monadic Way Part I and The Monadic Way Part II.

See below for some introductory remarks. Contents Meet Bob The Monadic Lover. Monad. Monads in Haskell can be thought of as composable computation descriptions.
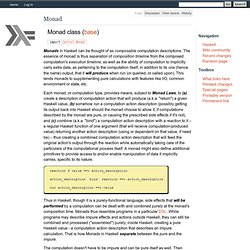
The essence of monad is thus separation of composition timeline from the composed computation's execution timeline, as well as the ability of computation to implicitly carry extra data, as pertaining to the computation itself, in addition to its one (hence the name) output, that it will produce when run (or queried, or called upon). Abstraction, intuition, and the “monad tutorial fallacy” While working on an article for the Monad.Reader, I’ve had the opportunity to think about how people learn and gain intuition for abstraction, and the implications for pedagogy.
The heart of the matter is that people begin with the concrete, and move to the abstract. Concrete monads 1 : Maybe, Either, list, IO. Why Do Monads Matter? « Sententia cdsmithus. (A Side Note: I’ve been formulating the final thoughts on this post for about a week now. In an entirely unrelated coincidence, a good friend of mine and fellow Haskell programmer, Doug Beardsley, ended up writing two posts about monads over the weekend as well. Weird! But don’t fret; this isn’t really the same thing at all. I’m not writing to teach Haskell programmers how to use monads. I’m writing about a kind of intuition about why these concepts turn out to matter in the first place. Category Theory for Software Development? Why Do Monads Matter? ZuriHac 2015 - Monads by Example. YouTube. A Fistful of Monads - Learn You a Haskell for Great Good! When we first talked about functors, we saw that they were a useful concept for values that can be mapped over.
Then, we took that concept one step further by introducing applicative functors, which allow us to view values of certain data types as values with contexts and use normal functions on those values while preserving the meaning of those contexts. In this chapter, we'll learn about monads, which are just beefed up applicative functors, much like applicative functors are only beefed up functors. When we started off with functors, we saw that it's possible to map functions over various data types. We saw that for this purpose, the Functor type class was introduced and it had us asking the question: when we have a function of type a -> b and some data type f a, how do we map that function over the data type to end up with f b?
The Comonad.Reader » Mirrored Lenses. Lenses are a great way to deal with functional references, but there are two common issues that arise from their use. There is a long-standing folklore position that lenses do not support polymorphic updates. This has actually caused a fair bit of embarrassment for the folks who'd like to incorporate lenses in any Haskell record system improvement.Access control. It'd be nice to have read-only or write-only properties -- "one-way" or "mirrored" lenses, as it were. Moreover, lenses are commonly viewed as an all or nothing proposition, in that it is hard to mix them with arbitrary user functions.Finally there is a bit of a cult around trying to generalize lenses by smashing a monad in the middle of them somewhere, it would be nice to be able to get into a list and work with each individual element in it without worrying about someone mucking up our lens laws, and perhaps avoid the whole generalized lens issue entirely.
We'll take a whack at each of these concerns in turn today. Haskell/Understanding monads. Monads are very useful in Haskell, but the concept is usually difficult for newcomers to grasp.