

Edexcel GCSE Mathematics A (2010) Decisions on regulating use of calculators in new gcses as and a levels. ETF MPP Solutions to exam-style questions: Statistics. Get the facts: GCSE reform. GCSE Maths (9-1) - J560 (from 2015) GCSE, AS and A level Assessment Objectives. 1.
GCSE assessment objectives Assessment objectives are part of the assessment arrangements for these qualifications. We adopt them into our regulatory framework through the subject-specific conditions that exam boards must comply with when designing their specifications. Jump to: 1.1 Ancient languages 1.2 Art and design 1.3 Citizenship studies | Objective | Requirements | Weighting | —- | —- | —- | | AO1 | Demonstrate knowledge and understanding of citizenship concepts, terms, and issues | 30% | | AO2 | Apply knowledge and understanding of citizenship concepts, terms and issues to contexts and actions | 30% | | AO3 | Analyse and evaluate a range of evidence relating to citizenship issues, debates and actions, including different viewpoints, to develop reasoned, coherent arguments and make substantiated judgments | 40% | ### Computer science 1.4 Dance 1.5 Design and technology 1.6 Drama 1.7 English language 1.8 English literature.
MEI > Teachers > Contextualisation Toolkit. Contextualising post-16 GCSE Mathematics: A toolkit for practitioners This resource is designed for teaching practitioners involved in planning and delivering post-16 GCSE Mathematics, including both specialist maths teaching practitioners and vocational teaching practitioners who wish to embed maths in their delivery.

The toolkit encourages these practitioners to make greater use of contexts in their delivery of post-16 GCSE Mathematics. It supports them in developing and using their own contextualised resources and encourages them to share their resources and to adapt and use resources that others have developed. The toolkit has been developed with funding from the Department for Education and in partnership with the Association of Employment and Learning Providers. In developing it we have worked closely with a range of providers from the Education and Training sector. Please use the link below to view a recording of the webinar which introduces the toolkit: Webinar - March 2015. Teacher support. Tricky crocodile maths question befuddles students - but can you answer it? Earlier this year, a maths exam sat by students in Scotland was deemed so difficult that the pass mark had to be lowered.
And now, a report has identified the chief culprit - a perplexing question about a crocodile stalking its prey. The pass mark for the new-look Higher maths exam - the Scottish equivalent of an A-level - was slashed to a lowly 34%. According to a report for the Scottish Qualifications Authority (SQA), the action was taken because of the overall difficulty of the test, as opposed to individual questions. However, the report, from the principal assessor in maths, does make specific reference to two questions which sparked outcry among students on social media. GCSE Maths Revision.
Maths Zone < Maths Zone - Free Cool Learning Games for School. Introducing the Maths OCR Team and the reformed GCSE Maths. GCSE maths reform - six things you need to know. Assessment stuff. Circles. Transformations of the Sine and Cosine Graphs. Transformations of the Sine and Cosine Graph – An Exploration By Sharon K.
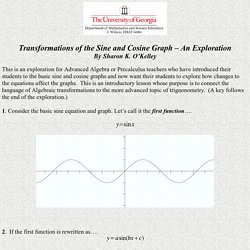
O’Kelley This is an exploration for Advanced Algebra or Precalculus teachers who have introduced their students to the basic sine and cosine graphs and now want their students to explore how changes to the equations affect the graphs. This is an introductory lesson whose purpose is to connect the language of Algebraic transformations to the more advanced topic of trignonometry. (A key follows the end of the exploration.) 1. 2. Then the values of a = 1, b = 1, and c = 0. Let’s find out what happens when those values change…. 3. Equation of blue graph Equation of red graph a. B. C. 4. Equation of purple graph Equation of green graph a. B.
C. D. 5. B. C. Bar modelling- a powerful visual approach for introducing number topics. Building on my recent post about a taxonomy for deep learning in maths, I have been trying to think a bit deeper myself about what each type of ‘deep learning link’ might look like.
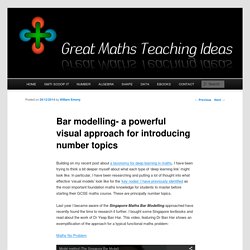
In particular, I have been researching and putting a lot of thought into what effective ‘visual models’ look like for the ‘key nodes’ I have previously identified as the most important foundation maths knowledge for students to master before starting their GCSE maths course. These are principally number topics. Last year I became aware of the Singapore Maths Bar Modelling approached have recently found the time to research it further. I bought some Singapore textbooks and read about the work of Dr Yeap Ban Har.
Quadratic Functions. How can you tell, by LOOKING at a quadratic function, if the vertex is going to be considered 'minimum' or 'maximum' and what exactly is the difference between the two vocabulary words?

Well, if you stop and thought about the two words, you just might be able to come up with a logical conclusion. Since a parabola is a U-shape, let's take a look at what this shape looks like in a drawing again and see if you can come up with a conclusion all on your own. Okay, now think of the two words: minimum and maximum. What do they mean? Which of the two parabolas do you think just might indicate minimum and which just might indicate maximum? If you think of a mountain or a valley, which words might fit minimum and maximum? Did you come up with the first one shows minimum and the second shows maximum?
What part of the equation will help you determine if the equation will show a minimum vs. maximum vertex? PS: Where have you see this information before? GCSE Bitesize: Factorising activity. Introduction to Geogebra. Draw Function Graphs - Plotter. Maths 2014 sow.