

Writing the code you need. Maths in IT #2: Venn diagrams. Hey everyone, welcome back to part two of the Maths in IT series.
I got a lot of positive response, so I guess I should just keep doing what I was already doing. This post will continue where part one left off, so if you haven’t read it I suggest you do so now before continuing. Here’s a quick cheat sheet with symbols I’ll use in this article: Explicit definition: Implicit definition: Maths in IT #1: Basic set theory.
Welcome back everyone.
Today I have a little something different for you. No new language or framework, but something that’s been around for millennia: maths. When asking programmers about maths you’ll find two kinds of people, those who say you don’t need maths to be a good programmer and those who say maths is essential. Personally I think both are true. For some applications and industries you really don’t need advanced maths, but go into robotics, machine learning, statistics, or that kind of thing and you’re going to need maths, lots of it.
Riemann-oppervlak. Ergodiciteit. Het begrip ergodiciteit betekent dat de eigenschappen van een systeem voor elke verschijningsvorm (bijvoorbeeld over tijd, plaats, of andere variatie) hetzelfde blijven; als het systeem lang genoeg gevolgd wordt, dan komen alle mogelijke toestanden voorbij.

Universal quantification. "∀" redirects here.
For similar symbols, see Turned A. Basics[edit] Constructal Theory Predicts Global Climate Patterns In Simple Way. DURHAM, N.C. -- A unifying physics principle that describes design in nature predicts, in surprisingly straightforward fashion, the basic features of global circulation and climate, according to researchers at Duke University's Pratt School of Engineering and the University of Evora in Portugal.
They said the new approach to climate may have important implications for forecasting environmental change. The researchers found that the "constructal theory" can predict the global circulation that determines the boundaries between desert and tropical forests as well as between temperate zones and the poles. Based only on the optimal flow of heat from the sun, the theory also predicts other climate characteristics, such as average wind speed and the average temperature difference between night and day.
The Story of Mathematics - A History of Mathematical Thought from Ancient Times to the Modern Day. Philosophy of mathematics. The terms philosophy of mathematics and mathematical philosophy are frequently used as synonyms.[1] The latter, however, may be used to refer to several other areas of study.
One refers to a project of formalizing a philosophical subject matter, say, aesthetics, ethics, logic, metaphysics, or theology, in a purportedly more exact and rigorous form, as for example the labors of scholastic theologians, or the systematic aims of Leibniz and Spinoza. Another refers to the working philosophy of an individual practitioner or a like-minded community of practicing mathematicians. Additionally, some understand the term "mathematical philosophy" to be an allusion to the approach to the foundations of mathematics taken by Bertrand Russell in his books The Principles of Mathematics and Introduction to Mathematical Philosophy. Recurrent themes[edit] Recurrent themes include: What is the role of Mankind in developing mathematics?
History[edit] Constructal law. Constructal law is a theory of the generation of design (configurations, patterns, geometry) in nature.
According to this theory, natural design and the constructal law unite all animate and inanimate systems.[1] The constructal law was stated by Adrian Bejan in 1996 as follows: "For a finite-size system to persist in time (to live), it must evolve in such a way that it provides easier access to the imposed currents that flow through it. "[2][3] The constructal law is receiving increased acceptance within the scientific community.[4] "Constructal" is a word coined by Bejan to describe the natural tendency of flow systems (e.g. rivers, trees and branches,[5] lungs, tectonic plates[6] and engineered forms[7]) to generate and evolve structures that increase flow access.[2][8] Introduction[edit] The constructal law was proposed in 1996 as a summary of all design generation and evolution phenomena in nature, bio and non-bio.
Manifestations[edit] Evolutionary design[edit] Evolution never ends. Game Theory. First published Sat Jan 25, 1997; substantive revision Wed May 5, 2010 Game theory is the study of the ways in which strategic interactions among economic agents produce outcomes with respect to the preferences (or utilities) of those agents, where the outcomes in question might have been intended by none of the agents.

Chaos theory. A double rod pendulum animation showing chaotic behavior.
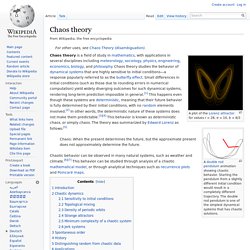
Starting the pendulum from a slightly different initial condition would result in a completely different trajectory. The double rod pendulum is one of the simplest dynamical systems that has chaotic solutions. Chaos: When the present determines the future, but the approximate present does not approximately determine the future. Chaotic behavior can be observed in many natural systems, such as weather and climate.[6][7] This behavior can be studied through analysis of a chaotic mathematical model, or through analytical techniques such as recurrence plots and Poincaré maps.
Introduction[edit] Chaos theory concerns deterministic systems whose behavior can in principle be predicted. Chaotic dynamics[edit] The map defined by x → 4 x (1 – x) and y → x + y mod 1 displays sensitivity to initial conditions.