

Articles. There is nothing wrong with rand per se, but there is a lot of confusion about what rand does and how it does it.
Shell And Wait. Shell And Wait This pages describes the VBA Shell function and provides a procedure that will wait for a Shell'd function to terminate.
The VBA Shell function can be used to start an external program or perform any operation for which you would normally use the Run item on the Windows start menu. The Shell function starts the command text and then immediately returns control back to the calling VBA code -- it does not wait for the command used in Shell to terminate. WriteExcel is dead. Long live Excel. Last week I released a new version of Excel::Writer::XLSX to CPAN that was 100% API compatible with Spreadsheet::WriteExcel.
Bc Command Manual. An arbitrary precision calculator language version 1.06 Description bc [ -hlwsqv ] [long-options] [ ] bc is a language that supports arbitrary precision numbers with interactive execution of statements.

There are some similarities in the syntax to the C programming language. This version of bc contains several extensions beyond traditional bc implementations and the POSIX draft standard. Laser Diode. 2-2-2.

Reliability Theory The well known bathtub curve describes the failure rate for most electrical devices (Fig. 2). In the initial stage, the failure ratio starts off high and decreases over time. Controlling brain cells with light. 21.01.15 - EPFL scientists have used a cutting-edge method to stimulate neurons with light.

They have successfully recorded synaptic transmission between neurons in a live animal for the first time. Neurons, the cells of the nervous system, communicate by transmitting chemical signals to each other through junctions called synapses. This “synaptic transmission” is critical for the brain and the spinal cord to quickly process the huge amount of incoming stimuli and generate outgoing signals. However, studying synaptic transmission in living animals is very difficult, and researchers have to use artificial conditions that don’t capture the real-life environment of neurons. Now, EPFL scientists have observed and measured synaptic transmission in a live animal for the first time, using a new approach that combines genetics with the physics of light. Activating neurons with light Recording neuronal transmissions Reference. Farey sequence. Symmetrical pattern made by the denominators of the Farey sequence, F8.
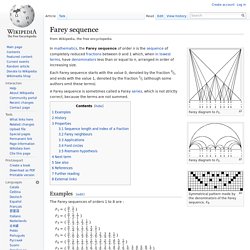
In mathematics, the Farey sequence of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size. Each Farey sequence starts with the value 0, denoted by the fraction 0⁄1, and ends with the value 1, denoted by the fraction 1⁄1 (although some authors omit these terms). Examples[edit] Neural networks and deep learning.
The human visual system is one of the wonders of the world.

Consider the following sequence of handwritten digits: Most people effortlessly recognize those digits as 504192. That ease is deceptive. In each hemisphere of our brain, humans have a primary visual cortex, also known as V1, containing 140 million neurons, with tens of billions of connections between them. And yet human vision involves not just V1, but an entire series of visual cortices - V2, V3, V4, and V5 - doing progressively more complex image processing. The difficulty of visual pattern recognition becomes apparent if you attempt to write a computer program to recognize digits like those above. Neural networks approach the problem in a different way. And then develop a system which can learn from those training examples.
Quoc Le’s Lectures on Deep Learning. Dr.

Quoc Le from the Google Brain project team (yes, the one that made headlines for creating a cat recognizer) presented a series of lectures at the Machine Learning Summer School (MLSS ’14) in Pittsburgh this week. This is my favorite lecture series from the event till now and I was glad to be able to attend them. The good news is that the organizers have made available the entire set of video lectures in 4K for you to watch. But since Dr. Le did most of them on the board and did not provide any accompanying slides, I decided to put the contents of the lectures along with the videos here. NYU Course on Deep Learning (Spring 2014) Deep Learning of Representations. #! Deep learning. Branch of machine learning Deep learning (also known as deep structured learning or differential programming) is part of a broader family of machine learning methods based on artificial neural networks with representation learning.
Learning can be supervised, semi-supervised or unsupervised.[1][2][3] Deep learning architectures such as deep neural networks, deep belief networks, recurrent neural networks and convolutional neural networks have been applied to fields including computer vision, speech recognition, natural language processing, audio recognition, social network filtering, machine translation, bioinformatics, drug design, medical image analysis, material inspection and board game programs, where they have produced results comparable to and in some cases surpassing human expert performance.[4][5][6] Artificial neural networks (ANNs) were inspired by information processing and distributed communication nodes in biological systems.
Definition[edit] Overview[edit] History[edit] Jitter. Jitter can be quantified in the same terms as all time-varying signals, e.g., root mean square (RMS), or peak-to-peak displacement. Also like other time-varying signals, jitter can be expressed in terms of spectral density (frequency content). Jitter period is the interval between two times of maximum effect (or minimum effect) of a signal characteristic that varies regularly with time. Jitter frequency, the more commonly quoted figure, is its inverse. ITU-T G.810 classifies jitter frequencies below 10 Hz as wander and frequencies at or above 10 Hz as jitter.[2] MMSIM 7 error connected with license file. DSP - Community Edition - Not for commericial use. MicroModeler DSP is a fast and efficient way to design digital filters. Use it to filter signals in the frequency domain for your embedded system MicroModeler DSP is Loading.
Please wait.... Here's a list of features to keep you busy while it loads... IIR Filter Types: Butterworth Chebyshev Inverse Chebyshev Bessel Elliptic High pass Low pass Band pass Band stop FIR Filter Design Methods Frequency Sampling Equiripple (Parks-McClellan) FIR Filter Specifications: High pass Low pass Band pass Band stop Hilbert Transform Differentiator Standard Filter Types Comb Filter Moving Average Filter Lth Band and Half Band Raised Cosine Blank Filter (Add Poles and Zeros) Stockholm International Water Institute. 2014 Stockholm Junior Water Prize The 2014 Stockholm Junior Water Prize International Final takes place during the World Water Week in Stockholm, August 31 – September 5, 2014. The award ceremony will take place September 3 at Grand Hôtel in the heart of Stockholm. Good luck to all finalists!
New prize sums for 2014. Digital Filter Design, Writing Difference Equations For Digital Filters, a Tutorial. ApICS LLC. Digital Filter Design Writing Difference Equations For Digital Filters Brian T. Boulter © ApICS ® LLC 2000 Difference equations are presented for 1st, 2nd, 3rd, and 4th order low pass and high pass filters, and 2nd, 4th and 6th order band-pass, band-stop and notch filters along with a resonance compensation (RES_COMP) filter. 1st. order normalized Butterworth low pass filter:
Finite impulse response. The impulse response (that is, the output in response to a Kronecker delta input) of an Nth-order discrete-time FIR filter lasts exactly N + 1 samples (from first nonzero element through last nonzero element) before it then settles to zero. FIR filters can be discrete-time or continuous-time, and digital or analog. Definition[edit] A direct form discrete-time FIR filter of order N. Infinite impulse response. Infinite impulse response (IIR) is a property applying to many linear time-invariant systems.
Common examples of linear time-invariant systems are most electronic and digital filters. Systems with this property are known as IIR systems or IIR filters, and are distinguished by having an impulse response which does not become exactly zero past a certain point, but continues indefinitely. Bending the Light with a Tiny Chip.