

Histoire de l'algèbre. L’algèbre a d’abord été une branche des mathématiques qui concernait les règles des opérations sur les nombres et la résolution des équations pour devenir plus tard une théorie des opérations puis des propriétés sur les êtres mathématiques en général.
Cette rubrique tente de retracer la longue épopée d'une discipline qui a commencé, il y a plus de 4000 ans, à l’époque de la civilisation babylonienne et qui aujourd’hui encore poursuit son évolution... Les initiateurs de l’algèbre : - Babyloniens et égyptiens - Chinois - Grecs - Indiens La naissance de l'algèbre dans le monde arabo-musulman : Nombre dix. Réflexions philosophico-mathématiques sur le Hasard [P.Cartier] Cours de mathématiques supérieures. Les kamites - Page 4. Rappel du premier message : "Les premiers mathématiciens de l’histoire universelle étaient africains !
De l’aveu des anciens, l’Afrique noire est le berceau des sciences mathématiques. Les premiers mathématiciens de l’histoire universelle étaient africains ! L’appréciation de nos Humanités Classiques Africaines et l’enseignement pédagogique de celles-ci implique que nous puissions léguer aux jeunes générations panafricaines des repères précis. Il en va de notre responsabilité d’adulte de satisfaire le plus précisément que possible, ce besoin d’information. Malheureusement les adultes actuels, qu’ils soient diplômés ou non, sont très loin de pouvoir apprécier leur très haut niveau de responsabilité dans la transmission de notre patrimoine intellectuel aux jeunes générations, tant l’aliénation culturelle et l’ignorance ont ravagé leur conscience. C’est pour y remédier que je souhaite vous faire découvrir certains d’entre eux. Les savants africains de la période pharaonique… Résolution des équations de degré 3 et 4.
Ce texte — qui reprend un exposé du séminaire Mathematic Park donné par l’auteur en octobre 2011 à l’occasion des célébrations du bicentenaire de la naissance d’Évariste Galois — propose de montrer quelques aspects de la résolution des équations algébriques de degré 3 et 4 à travers une petite promenade mathématique qui commence au XVIème siècle avec les mathématiciens de la Renaissance italienne et se termine au XVIIIème siècle avec les travaux de Lagrange.
Introduction Avant d’aborder la résolution des équations proprement dite, il est nécessaire de préciser de quelles équations on parle et ce que l’on entend par « résolution ». Qu’est-ce qu’une équation algébrique ? Une équation algébrique (ou polynomiale) est une équation de la forme x^n + a_{n-1} x^{n-1} + \cdots + a_1 x +a_0= 0. Les mathématiques au XVIIIe siècle dans les manuels d’enseignement : Du « Pourquoi ? » au « Comment ? » L’enseignement des mathématiques en France au XVIIIe siècle Les études au XVIIIe siècle et depuis le Moyen-âge, étaient, en dehors des écoles militaires, essentiellement organisées dans des collèges.

La scolarité complète, qui aboutissait au niveau de la maîtrise ès arts, durait environ six ans, et le parcours décrivait successivement les classes de Grammaire – quelquefois accomplies dans des écoles avant le collège -, Humanités, Rhétorique I et II, Philosophie I et II. Les collèges étaient appelés « de plein exercice » ou « petits collèges », suivant leur capacité à offrir ou non le cursus complet. La maîtrise ès arts était décernée après des examens qui suivaient la classe de Philosophie II, si le collège était autorisé par l’Université à la collation des grades [1]. Cette étude comprenait surtout la géométrie élémentaire et un peu d’arithmétique et d’algèbre. Histoire des mathématiques. Villeneuve retour au sommaire La preuve cartésienne de la quadrature du cercle Autre Ressource sur CultureMATH.
L'histoire des mathématiques. L'origine des mathématiques est très lointaine. Mais pour tout le temps qui précède l'invention de l'écriture, il semble difficile d'énoncer autre chose que des généralités, seulement étayées indirectement par quelques témoignages archéologiques (successions d'entailles ou de marques qui peuvent faire penser à un comptage, etc.) ou par les analogies que l'on peut tirer des études ethnologiques : on savait compter; ici, plusieurs systèmes de numération ont pu être utilisés (numération décimale, duodécimale, sexagésimale, etc.), là, on a pu s'en tenir à l'usage de quatre nombres seulement (un, deux, trois, « beaucoup »); on devait aussi connaître quelques principes d'arpentage des champs cultivés, imposés par le développement de l'agriculture. En tout cas, il est frappant de constater que l'invention de l'écriture est partout étroitement liée à des préoccupations mathématiques, ou du moins comptables.
(Pi) la valeur approchée 3. Henri Poincaré, L'invention mathématique. Nous commémorons en cette année les 100 ans de la mort d’Henri Poincaré.

Cet anniversaire est un prétexte idéal pour présenter son œuvre dense qui a influencé la science moderne. Poincaré a publié quatre livres philosophiques : La Science et l’Hypothèse (1902), La Valeur de la Science (1905),Science et Méthode (1908) etDernières Pensées (posthume) (1913). La plupart des chapitres de ces livres reprennent des conférences de Poincaré et sont donc relativement indépendants les uns des autres. Nous vous proposons de retrouver toutes les semaines l’enregistrement d’un chapitre d’un de ces livres. L’ordre suivi par le lecteur sera quelque peu aléatoire, au gré de son humeur. Henri Poincaré, Science et Méthode, Livre premier, chapitre 3 : L’invention mathématique. « La genèse de l’Invention mathématique est un problème qui doit inspirer le plus vif intérêt au psychologue. Écouter le podcast : MATHEMATICIENS CELEBRES : Maths-rometus, Mathématiciens, Histoire des maths, illustrations, Mathématiques, Maths, Jean-Luc Romet, Math.
CIVILISATIONS MATHEMATICIENNES : Maths-rometus, Histoire des maths, Illustrations, Maths, Mathématiques, Jean-Luc Romet, Math. Préhistoire (vers 35000 avant JC - vers 3000 avant JC) Mésopotamie (vers 3000 avant JC - vers 200 avant JC) Egypte (vers 3000 avant JC - vers 330 avant JC) Chine (vers 1300 avant JC - vers 1300 après JC) Grèce (vers 700 avant JC - vers 500 après JC) Mayas (vers 300 avant JC - vers 900 après JC)
HISTOIRE DES MATHS : Maths-rometus, Histoire des mathématiques, Illustrations, Images, Mathématiciens, Mathématiques, Maths, Jean-Luc Romet, Math, Maths-rometus. Les mathématiques furent essentiellement créées parce que l'on en avait besoin, et elles ont été bien souvent un outil, ne l'oublions pas! De nombreux mathématiciens étaient aussi des philosophes, des astronomes, des historiens et même des poètes, particulièrement en Grèce et en Europe au Moyen Age. Ils furent aussi de grands physiciens jusqu'au XIXème siècle. Aujourd'hui, on est encore obligé de créer de nouveaux concepts mathématiques pour répondre à la demande de la haute technologie.
Les mathématiques ont donc été un outil pour les autres sciences, elles les ont souvent suivies. Quand les mathématiques ne répondirent pas à un réel besoin, elles finirent toujours par permettre de résoudre de nouveaux problèmes qui se posèrent bien plus tard… Il est donc arrivé aussi qu'elles précèdent les grandes découvertes. Menu Histoires dans Mathématiques magiques. Mathématiques arabes. Un article de Wikipédia, l'encyclopédie libre.
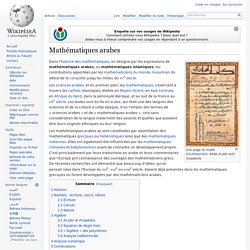
Une page du traité d'al-Khwarismi, Kitab al jabr wa'l muqabala Dans l'histoire des mathématiques, on désigne par les expressions de mathématiques arabes, ou mathématiques islamiques, les contributions apportées par les mathématiciens du monde musulman du début de la conquête jusqu'au milieu du XVe siècle. Les sciences arabes, et en premier plan, les mathématiques, s'exercent à travers les califats islamiques, établis en Moyen-Orient, en Asie centrale, en Afrique du Nord, dans la péninsule ibérique, et au sud de la France au VIIIe siècle. Les textes sont écrits en arabe, qui était une des langues des sciences et de la culture à cette époque, d'où l'emploi des termes de « sciences arabes » et de « mathématiques arabes », cela sans considération de la langue maternelle des savants et quelles que puissent être leurs origines ethniques ou leur religion.
§Histoire[modifier | modifier le code] §Écriture[modifier | modifier le code] Version arabe. Qu'est-ce qu'un mathématicien ? Les mathématiques françaises, au moment où s'exprime André Lichnerowicz, au milieu des années 1960, connaissent une très grande renommée, caractérisée par l'audience de leurs publications.
Depuis 1945, plusieurs mathématiciens ont été consacrés par la médaille Fields, équivalent du prix Nobel de mathématiques. Pour introduire au travail d'un mathématicien, André Lichnerowicz choisit de présenter une branche des mathématiques : l'algèbre. Encore aujourd'hui, l'algèbre au sens courant et dans l'enseignement primaire et secondaire désigne le calcul et la résolution d'équations. Que sont les mathématiques? Portail:Mathématiques. Une page de Wikipédia, l'encyclopédie libre.
Polyh.pdf. Bienvenue sur ChronoMath, une chronologie des mathématiques. Histoire des mathématiques. Un article de Wikipédia, l'encyclopédie libre. L’histoire des mathématiques s'étend sur plusieurs millénaires et dans de nombreuses régions du globe allant de la Chine à l’Amérique centrale. Jusqu'au XVIIe siècle, le développement des connaissances mathématiques s’effectue essentiellement de façon cloisonnée dans divers endroits du globe. À partir du XIXe et surtout au XXe siècle, le foisonnement des travaux de recherche et la mondialisation des connaissances mènent plutôt à un découpage de cette histoire en fonction des domaines mathématiques. Préhistoire[modifier | modifier le code]
Programme 2011 - Un texte, un mathématicien. Cycle de conférences organisées par la Bibliothèque nationale de France et la Société Mathématique de France.
Quatre conférences de mathématiques vont être organisées à l'attention du grand public, des professeurs du second degré et des lycéens et étudiants au cours de l'année 2011. Elles auront lieu le mercredi à 18h30 à la BNF (site F. -Mitterrand, Grand auditorium, Hall Est, Quai François-Mauriac, Paris 13). Le conférencier choisit un texte mathématique datant de plusieurs dizaines d’années, voire bien plus, qui l’a particulièrement influencé. A partir de ce texte, de son auteur et de son histoire, le conférencier montre de quelle manière une problématique ancienne débouche sur des questions actuelles et des recherches mathématiques en cours.
Les films des conférences 2010 (site d'Animath) Télécharger l'affiche (format pdf 864 Ko) Le cycle est organisé en partenariat avec France Culture, et Animath. Inscription obligatoire pour les groupes scolaires : voir ici. IAF. Espaces courbes de Gauss à Perelman en passant par Einstein. Mêlant histoire et mathématiques, ces conférences permettent à un large public de découvrir les mathématiques contemporaines. Après le très grand succès des cinq années précédentes, le cycle « Un texte, un mathématicien » accueille cette année une mathématicienne et trois mathématiciens, tous chercheurs de renommée internationale. Cycle organisé avec la Société Mathématique de France, en partenariat avec France Culture, le magazine Tangente et Animath. Karl Friedrich Gauss est un des plus importants mathématiciens à la charnière des XVIIIe et XIXe siècles. Il s’est particulièrement intéressé à la géométrie des surfaces, par exemple : comment mesurer que la Terre n’est pas exactement sphérique sans l’observer de l’extérieur ?
La notion d’espace courbe s’est avérée centrale depuis lors : travaux de Bernhard Riemann au XIXe siècle, relativité générale d’Albert Einstein, et tout récemment solution de la conjecture de Poincaré par Perelman. Images des mathématiques. Département de Mathématiques d'Orsay. MATHCURVE.COM. Bienvenue sur ChronoMath, une chronologie des mathématiques.